Bonjour,
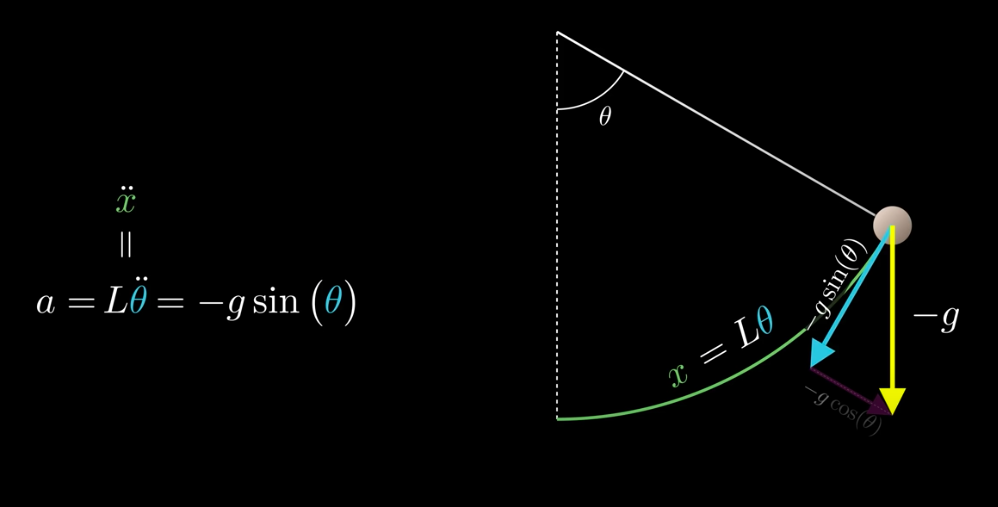
En guise d'introduction concernant les équations différentielles, j'ai regardé cette vidéo et plus particulièrement la partie définissant l'équation différentielle d'un pendule (à 7:00).
J'ai du mal à comprendre pourquoi
Car si je prends la deuxième dérivée de
, j'obtiens 0.
Est-ce que quelqu'un peut m'expliquer pourquoi ce que je dis est faux ? Ça a l'air tout con, mais je bloque là-dessus depuis un moment...
-----