Bonjour à tous
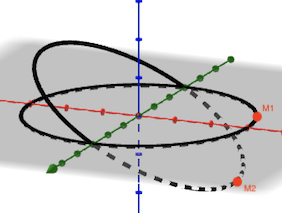
j'ai un exercice d'électromagnétisme portant sur un cercle chargé d'une densité linéique de charges uniforme positive pour x négative, et pour x positive elle est négative. Je me demande pourquoi une invariance par rotation autour de (Ox) n'existe pas?
Il me semble qu'une telle rotation contrairement à celles des autres axes ne change pas l'emplacement d'un point M quelconque par rapport à x, et par conséquent sa densité reste constante
Merci d'avance
Bonsoir
Peux-tu préciser en quel point on te demande de déterminer le vecteur champ ?
L'étude des invariances est surtout utile quand on se pose la question de l'intérêt du théorème de Gauss...
Dernière modification par petitmousse49 ; 16/08/2020 à 21h28.
Merci pour ton intérêt petit mousse
En fait cet exercice porte sur le chapitre 1. On y étudie les symétries en abstraction du champ électrostatique qu'on a pas encore abordé
Il faudrait faire un schéma : à lire entre les lignes (mais justement j'ai peut-être mal lu), l'axe x est un diamètre du cercle.
Si on tourne un cerceau autour d'un de ces diamètres, même indépendamment des charges, il est évident que cela change qqch.
Dans le cas de deux demi-cercles chargés, il existe une symétrie par rapport à l'axe x.Envoyé par Wiame 1
Il n'y a pas d'invariance par rotation, car les charges changent de place dans l'espace, pour qu'une telle invariance existe, il faudrait deux hémisphères chargés en surface.
Comprendre c'est être capable de faire.
Effectivement. (Ox) est un diamètre du cercle. Mais je ne vois pas pourquoi tourner un cercle autour se son diamètre ne le laissera pas invariant. Qu'est-ce qui pourra changer?
Merci pour ton intérêt
Vous voulez dire que si on a une figure dans le plan il ne faut considérer que ses rotations dans ce plan, et non pas dans l'espace?
De toute façon, j'avais un exercice avec deux hémisphères de charges opposées symétriques par rapport à (Ox) mais qui ne présentait pas d'invariance par rotation autour de cet axe, à croire au corrigé. Et je ne vois pas pourquoi
Merci pour ton intérêt
Ce n'est pas une "figure", mathématiquement le cercle dans n'importe quelle position reste un cercle, mais d'un objet et si la roue de votre vélo est à l'horizontale, ce n'est pas la même chose que si elle est à la verticale.
Je comprend ceci : face rouge positive, grise négative, si on tourne autour de Ox, la distribution de charges change.
Capture d’écran.png
Quelle définition donnez-vous (utilisez-vous) d'invariant ?
Et si on la fait tourner autour de (AB)?
J'utilise invariant dans le sens de l'invariance de la distribution de charges.
Autour de AB, cela marche, j'avais mal compris l'axe la définition de l'axe Ox
Pourquoi alors ici c'est pas le cas?
Le deuxième cercle est obtenu par rotation autour de l'axe Ox (en vert) : est-ce que la distribution de charges est la même dans le deux cas ?
CercleOx.png
Je trouve qu'elle reste la même
Qu'est-ce qui change?
La seule rotation qui pourrait laisser le cercle invariant serait une rotation autour de l'axe z, mais comme le cercle n'a pas une charge uniforme, cette rotation déplacera les charges.
Comprendre c'est être capable de faire.
Est-ce que la charge au point M1 est la même dans les deux cas ?
Je dirai que non, disons +q dans l'état initial et 0 dans l'état final, on ne peut pas vraiment dire que la charge est invariante.
