Bonsoir,
j'ai un petit exercice à faire actuellement et je bloque complètement. Je suis des cours de propa-electro et je dois démontrer une identité remarquable(voir photo). J'ai pour l'instant fait : [notation : tri pour le laplacien] , tri(fg) = div(grad(fg)) = div(fgrad(g)+ggrad(f)) = fdiv(grad(g)) + gdiv(grad(f)) = f tri(g) + g tri(f). Il me manque la partie 2grad(f) grad(g) mais je ne sais pas comment faire. Pourriez vous m'aider svp ?
voici la demonstration à réaliser :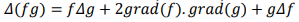
-----




 on dérive d'abord f en considérant
on dérive d'abord f en considérant