Les accélérations et les forces de Coriolis et d'entraînement

[Amanuensis]

Le est le projeté.

Sur un jour sidéral.
-----

[Amanuensis]

Euh. Faut aussi apporter les corrections de la relativité. (C'est comme çà que je le dis, Amanuensis).

Pourtant je n'en parle pas ici. Il y a bien d'autres "petits" problèmes avec le modèle de Newton !

D'ailleurs j'aimerais bien voir et examiner la liste des hypothèses pour une question bien posée telle que ce soit celle à laquelle Calculair cherche à répondre !

Genre définition précise du champ de gravitation utilisée (e.g., comme une formule donnant les coordonnées du champ en fonction de la position dans le référentiel terrestre ou géocentrique).

Genre définition précise de la forme de la Terre, et de la différence d'altitude. (e.g., équation de la surface d'altitude x, d'une part avec x celle du sommet de la tour, et d'autre part avec x celle de la surface "au pied" de la tour.

Car ces données sont nécessaires pour le calcul, en méca classique, dans le géocentrique pris comme galiléen (et donc nécessaires pour tout calcul de même fin):

1) Calcul de la vitesse initiale au lâcher

2) Calcul de la chute connaissant la condition initiale calculée en 1) ; (c'est le calcul d'une orbite dont on a donné un point et une vitesse à ce point, donc une trajectoire elliptique),

3) Calcul de l'événement "arrivée au sol", soit le lieu et la date de l'intersection entre l'orbite calculée en 2) et la surface d'altitude "pied de la tour".

4) et enfin, calcul de la distance entre le lieu trouvé en 3) et le lieu "vertical du sommet de la tour", soit l'intersection de la surface "pied de la tour" et de la verticale passant par le sommet de la tour.

[calculair]

Bonjour,

La TFL ce n'est pas la tour de Pise !!!

Elle est verticale, donc selon le rayon terrestre

Je vais réfléchir pour enlever toute ambiguïté ...

Par ailleurs les autres effets comme la rotation au tour du soleil et de la galaxie sont hyper négligeable et les effets relativistes aussi ...

J'espère que pour ce problème de mécanique, on finira par trouver une cohérence selon la manière dont on l'approche.....

On pourrait peut être aussi tenter faire le calcul comme un satellite qui tombe sur terre ..... Cela me parait encore plus délicat ....

Bonjour

Calculair.

Ton dessin n'est pas correct, je pense.

Voilà Ce que moi, je vois.
Pièce jointe 434890

Le trait vert, c'est la tour Eiffel telle qu'elle est dans ton premier calcul. Dans le référentiel où on regarde la terre tourner (voir l'équateur et le tropique du cancer).
Et l'objet part de là dans la direction Z (ou moins Z; j'ai pas le sens de rotation de la terre dans ma tête). Si X est dans le plan de l'équateur. Et Y l'axe pole sud. Pole nord.

Et là, tu peux commencer à faire des calculs.
Quand tu auras finis.............
Je te dirai que la terre tourne aussi autour du soleil.
Et puis que notre galaxie tourne autour de Sirus.
Et puis? On n'en sait rien.......................... .............................. .............

(Merci Amanuensis...)

Et comme tu dis dans le slogan de tous tes messages, en bas:
En science " Toute proposition est approximativement vraie " ( Pascal Engel)

Là tu es avec Newton.
Euh. Faut aussi apporter les corrections de la relativité. (C'est comme çà que je le dis, Amanuensis).
Et peut être qu'un jour (on mesurera encore plus précis), il y aura autre chose.....

86cat

PS: pour la tour Eiffel penchée (*), Gts2 a fait le calcul. C'est peanuts la différence.................... .............
(*): coucou Galilée.

[calculair]

Nos messages se sont croisés

Oui on suppose ici une terre homogène parfaitement sphérique ,tournant sur elle même ( seulement )....

C'est déjà assez délicat pour nous pour être sur d'avoir le bon résultat ...

Pourtant je n'en parle pas ici. Il y a bien d'autres "petits" problèmes avec le modèle de Newton !

D'ailleurs j'aimerais bien voir et examiner la liste des hypothèses pour une question bien posée telle que ce soit celle à laquelle Calculair cherche à répondre !

Genre définition précise du champ de gravitation utilisée (e.g., comme une formule donnant les coordonnées du champ en fonction de la position dans le référentiel terrestre ou géocentrique).

Genre définition précise de la forme de la Terre, et de la différence d'altitude. (e.g., équation de la surface d'altitude x, d'une part avec x celle du sommet de la tour, et d'autre part avec x celle de la surface "au pied" de la tour.

Car ces données sont nécessaires pour le calcul, en méca classique, dans le géocentrique pris comme galiléen (et donc nécessaires pour tout calcul de même fin):

1) Calcul de la vitesse initiale au lâcher

2) Calcul de la chute connaissant la condition initiale calculée en 1) ; (c'est le calcul d'une orbite dont on a donné un point et une vitesse à ce point, donc une trajectoire elliptique),

3) Calcul de l'événement "arrivée au sol", soit le lieu et la date de l'intersection entre l'orbite calculée en 2) et la surface d'altitude "pied de la tour".

4) et enfin, calcul de la distance entre le lieu trouvé en 3) et le lieu "vertical du sommet de la tour", soit l'intersection de la surface "pied de la tour" et de la verticale passant par le sommet de la tour.

[Amanuensis]

Oui on suppose ici une terre homogène parfaitement sphérique ,tournant sur elle même ( seulement )....

C'est déjà assez délicat pour nous pour être sur d'avoir le bon résultat ...

Cela rajoute des pièges. Par exemple la surface du sol au pied de la tour n'est pas perpendiculaire à la verticale. (Faire l'hypothèse de l'identité entre la surface d'altitude donnée et une équipotentielle de pesanteur a des avantages !)

Cela ne change pas la question de l'approximation de l'orbite elliptique à je ne sais pas trop quoi.

Plus généralement ce n'est pas cohérent, la forme non sphérique de la Terre est une conséquence de la rotation de la Terre.

Ceci dit, cela semble donner (avec quelques trucs en plus) ce qu'il faut pour un calcul dans le géocentrique...

[invite968be57d]

Calculair

Moi, je me suis fait une raison.
J'ai ouvert une bible de mécanique (Gruber et Benoit) et j'ai lu à Coriolis.
J'ai lu le document de GTS2 aussi.
Et j'ai fait mon petit calcul. Pour me faire une idée de la distance et de la durée.
Dans le document de GTS, il y a une approximation (la terre y est plate) et une correction (l'effet recul...)
Et bon, je laisse faire les spécialistes (mathématiciens...)

Et si tu relis Amanuensis, il y a encore d'autres corrections. Le document de Gts en montre "autrement".....

Pour moi, c'est "nothing more". "Out". J'ai connu la VHF.

Chapeau pour la présentation du document

86cat

[Amanuensis]

Oui on suppose ici une terre homogène parfaitement sphérique ,tournant sur elle même ( seulement )....

Dans mes termes (et avec quelques ajouts explicités):

- Altitude = distance au centre

- Surface d'altitude donnée = sphère parfaite

- Champ gravitationnel = de symétrie parfaitement sphérique, en 1/d², d étant la distance au centre

La question est alors sur le lieu d'arrivée à l'altitude x après une chute libre d'un objet partant, immobile dans le terrestre, à l'altitude x + 300 m

Le calcul principal (dans le géocentrique) reste le calcul d'orbite, calcul classique du problème à deux corps.

[calculair]

on va finir par comprendre les erreurs des cibles des bombes lachées des avions durant la 2° guerre mondiale....

Cela rajoute des pièges. Par exemple la surface du sol au pied de la tour n'est pas perpendiculaire à la verticale. (Faire l'hypothèse de l'identité entre la surface d'altitude donnée et une équipotentielle de pesanteur a des avantages !)

Cela ne change pas la question de l'approximation de l'orbite elliptique à je ne sais pas trop quoi.

Plus généralement ce n'est pas cohérent, la forme non sphérique de la Terre est une conséquence de la rotation de la Terre.

Ceci dit, cela semble donner (avec quelques trucs en plus) ce qu'il faut pour un calcul dans le géocentrique...

[Amanuensis]

Annulé, erreur, ...

[calculair]

Bravo pour ta rigueur de Language et les précisions sur les termes utilisés.

Si tu veux traiter le problème comme un calcul d'orbite , il y a lieu également de garder les termes comme tu les as définis

J'ai quand même l'impression que ce type de calcul serait un super complément à cette approche, mais bien plus délicat.

Je pense que l'on devrait traiter la formule de Binet qui traite ce type de problème... J'avoue ne pas avoir le courage de me lancer dans cette approche....

Dans mes termes (et avec quelques ajouts explicités):

- Altitude = distance au centre

- Surface d'altitude donnée = sphère parfaite

- Champ gravitationnel = de symétrie parfaitement sphérique, en 1/d², d étant la distance au centre

La question est alors sur le lieu d'arrivée à l'altitude x après une chute libre d'un objet partant, immobile dans le terrestre, à l'altitude x + 300 m

Le calcul principal (dans le géocentrique) reste le calcul d'orbite, calcul classique du problème à deux corps.

[harmoniciste]

Je precise , en effet selon le sens de vol de l'avion la force complémentaire due à Coriolis change de sens .

Bonsoir
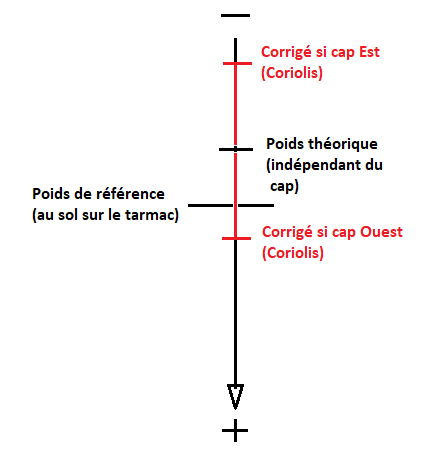
Je n’avais pas clairement saisi que votre référence était le poids incluant une force centrifuge visant le centre d’une Terre immobile.
Cette présentation m'a perturbé car la référence de poids est généralement la force au repos sur le tarmac.
Mais vous avez raison, les corrections de Coriolis s'appliquent à une Terre immobile dans l'espace, ce qui n'enlèvent pas la force centrifuge due au suivi de la courbure terrestre.
Ainsi, pour ramener votre résultat au poids de l'avion au repos sur le tarmac, il faut lui enlever la différence due au suivi de la courbure de la terre.
A 250 m/s, et un rayon terrestre de 6400 km, cela diminue le poids de 0.097% et c'est alors un surpoids de 0.26% - 0.097% = 0.16% que subit l'avion lorsqu'il vole vers l'Ouest, par rapport à son poids au repos.

Mon raisonnement est plutôt celui-ci:
L'accélération centrifuge au repos sur le tarmac étant déjà V[²/R, avec R = 4,5.10⁶ sous la latitude de 45°, et V₀ = 329 m/s, elle n’est plus que (79 m/s)²/R en vol vers l'Ouest. La différence vaut alors 23.10^-3 orientée vers l’axe de rotation de la Terre, ce qui donne verticalement 23.10^-3*Cos (45°) ou 0,16% de supplément par rapport au poids au repos.
Nos résultats sont identiques.
En vol vers l’Est, on trouverait 0.54 % d’allègement par rapport au poids sur le tarmac

[calculair]

pour moi lorsque on mesure g il y a la force de gravitation corrigée de la force centrifuge

[Amanuensis]

pour moi lorsque on mesure g il y a la force de gravitation corrigée de la force centrifuge

C'est l'approche "officielle", tous les textes sérieux le présentent ainsi. Simplement parce que c'est ce qu'on ressent, ce dont on constate les effets, ce qu'on peut mesurer, avec un "gravimètre", par exemple. La force de gravitation ne peut être que calculée.

Prendre g, l'accélération de la pesanteur, pour autre chose, ne peut qu'amener des difficultés conceptuelles ! (Pas nécessairement grave, ça dépend de ce qu'on en fait.)

[calculair]

Bonjour,

En effet tu as raison. De plus je n'avais pas totalement conscience de ce fait.

On pourrait par exemple ce demander l'écart d'angle du fil à Plomb à Paris entre la direction du Fil à Plomb et le rayon terrestre ( en supposant la terre Sphérique et homogène )

C'est l'approche "officielle", tous les textes sérieux le présentent ainsi. Simplement parce que c'est ce qu'on ressent, ce dont on constate les effets, ce qu'on peut mesurer, avec un "gravimètre", par exemple. La force de gravitation ne peut être que calculée.

Prendre g, l'accélération de la pesanteur, pour autre chose, ne peut qu'amener des difficultés conceptuelles ! (Pas nécessairement grave, ça dépend de ce qu'on en fait.)

[harmoniciste]

pour moi lorsque on mesure g il y a la force de gravitation corrigée de la force centrifuge

Nous sommes bien d'accord sur ce point.
Cependant en écrivant "393 kg c'est la charge complémentaire..." dans votre document post#7, cette présentation me parait tendancieuse en ce qu'est laisse croire que le poids de l'avion (M*g) est accru de cette valeur lors d'un vol vers l'Ouest, quand ce n'est que 278 kg. Et il laisse sous silence l'allègement bien plus conséquent de 810 kg lors d'un vol est vers l'Est. Parti pris étonnant.

[calculair]

Bonjour,

En complement, je voulais bien prendre conscience des effets de la gravitation pure et celui des effets centrifuges.

J'ai donc fait un calcul en utilisant les données trouvées sur le net

Le résultat n'est pas 100 % satisfaisant

[Amanuensis]

Nous sommes bien d'accord sur ce point.

On se le demande ...

Cependant en écrivant "393 kg c'est la charge complémentaire..." dans votre document post#7, cette présentation me parait tendancieuse en ce qu'est laisse croire que le poids de l'avion (M*g) est accru de cette valeur lors d'un vol vers l'Ouest, quand ce n'est que 278 kg. Et il laisse sous silence l'allègement bien plus conséquent de 810 kg lors d'un vol est vers l'Est.

C'est désespéré...

L'approche de Calculair est correcte, l'effet est linéaire, et donc symétrique par rapport à l'allègement de 0, c'est à dire au cas à vitesse nulle relative à la Terre.

[gts2]

A priori le problème est dans la masse de la terre : avec M = 5,9736e24 kg (wikipedia), on trouve bien un g raisonnable.

Où as-tu trouvé M = 6596 000 000 000 000 millions tonnes ?

[harmoniciste]

On pourrait par exemple ce demander l'écart d'angle du fil à Plomb à Paris entre la direction du Fil à Plomb et le rayon terrestre ( en supposant la terre Sphérique et homogène )

La réponse me semble simple:
A Paris (latitude 48°) la distance à l'axe de rotation est 4280 km et la vitesse tangentielle est 311 m/s d'où une accélération axifuge de 0,22% g , et l'accélération transversale est alors 0.22% Sin(48°) = 0,17% g
L'écart du fil à plomb avec le rayon de la Terre supposée sphérique est donc 0.0017 rd ou environ 0.1 degré vers le Sud

[calculair]

les données seraient fausses ....http://users.skynet.be/fa274406/text...nees_terre.htm

[gts2]

les données seraient fausses ...

Manifestement oui, tous les autres sites donnent des valeurs différentes de celle-ci (et proches entre elles)

[Amanuensis]

tonne américaine, 907 kg, peut-être

[harmoniciste]

L'approche de Calculair est correcte, l'effet est linéaire, et donc symétrique par rapport à l'allègement de 0, c'est à dire au cas à vitesse nulle relative à la Terre.

Allons, allons.
Coriolis apporte une correction par rapport à un calcul effectué sans rotation de la Terre dans l'espace. Cela n'évite pas de devoir considérer la vitesse du mobile relative à la Terre. Or, les 250 m/s de l'avion créent une inévitable centrifugation diminuant déjà le poids de l'avion en vol, quel que soit son cap.
Dès lors, la correction n'est pas symétrique par rapport au poids sur le tarmac

[Amanuensis]

Allons, allons.
Coriolis apporte une correction par rapport à un calcul effectué sans rotation de la Terre dans l'espace. Cela n'évite pas de devoir considérer la vitesse du mobile relative à la Terre. Or, les 250 m/s de l'avion créent une inévitable centrifugation diminuant déjà le poids de l'avion en vol, quel que soit son cap.
Dès lors, la correction n'est pas symétrique par rapport au poids sur le tarmac

Je répète, désespérant. Rien à dire de plus, tous les arguments ont déjà été proposés.

[gts2]

Je pense que le problème soulevé est qu'une trajectoire d'avion à altitude constante est une trajectoire non rectiligne, il y a donc une accélération centripète.

[Amanuensis]

Si peut-être ?

Il y a une seule accélération d'entraînement (1), on la décompose entre une partie indépendante de la vitesse et une partie dépendant de la vitesse (linéaire en la vitesse, donc nulle à vitesse nulle). (La première est l'accélération axifuge, et la seconde l'accélération de Coriolis.)

Cela n'a pas de sens de séparer les deux.

(1) On parle dans ce fil d'un référentiel en rotation uniforme

[Amanuensis]

Je pense que le problème soulevé est qu'une trajectoire d'avion à altitude constante est une trajectoire non rectiligne, il y a donc une accélération centripète.

Je ne pense pas. Juste un problème avec la notion de poids : selon qu'on prend "l'allègement" relatif à l'accélération de la gravitation, ou relatif à l'accélération de la pesanteur. Or "poids" signifie l'effet de l'accélération de la pesanteur.

[gts2]

Il y a une seule accélération d'entraînement

Là on tombe sur un problème de vocabulaire ou de définition (et donc sans solution), pour moi l'accélération d'entrainement est l'accélération du point coïncident (comme son nom "entrainement" l'indique) à laquelle il faut ajouter Coriolis.
Si la définition d'accélération d'entrainement comprend l'accélération de Coriolis, pourquoi pas.

[harmoniciste]

J'ai donc fait un calcul en utilisant les données trouvées sur le net

Calculair, dans votre pdf "le vrai g local" un angle de 0.002 rd vaut 0.4 degré . Pour moi 0.002 rd vaut 0.11 degré

Et j'ajoute ce croquis pour Amanuensis:

[calculair]

Bonjour,

Au lieu de faire les calcul sur la calculette du téléphone, une page Excel est plus pratique et sur....

OK tu a raison pour les 0,1 ° , bon cela c'est pour la beauté de la chose.....

En effet je n'ai pas encore refait le calcul, en toute rigueur il faut tenir compte de l'effet centrifuge du au vol

Cet effet est identique dans un sens ou dans l'autre en supposant les vent nuls

Il reste l'accélération de Coriolis qui change de sens selon le sens du vol ...

Ce qui compte c'est l'excès de poids apparent sur la consommation de carburant