Optique physique FFT 2D

[gts2]

J’avais aussi ajouter que pour passer en image d’angle de phase il suffit de multiplier l’image par 2pi

Manifestement le 2 pi est déjà incorporé (les valeurs vont de -5,4 à +5,4

Voilà ce qu'on obtient à partir des données du fichier phase.fit


-----

[Choc mou]

Et comment obtenez-vous w si ce n'est par un polynôme de Zernicke ?

Et donc, @B4lbu n'a pas tord, tant que vous ne nous aurez pas expliqué comment vous obtenez w (puisque ce n'est pas avec un polynôme de Zernicke), on ne pourra avancer d'un iota.

«Et comment obtenez-vous w si ce n'est par un polynôme de Zernike ?»

Et bien désolé, je n’avais pas compris le problème sous cet angle et je ne comprends pas cette question. Pourquoi faut-il obligatoirement passer par le calcul des coefficients de zernike*?
Sans rentrer dans les détails mathématiques (que je maîtrise pas forcément), pour moi les zernikes c’est une décomposition d’un front en coefficients. Donc c’est une analyse serte très utile mais qui aussi fait une reconstruction du front. Il faut alors beaucoup de terme pour se rapprocher de l’original.
Par exemple si l’on part d’un interférogramme analysé avec le Freeware DFTFringe le résultat DFT la surface déformée obtenue, est plus précis que celle issu des zernikes même avec 42 termes.

Hors dans l’exemple on a déjà cette image du front. Et c’est quoi une image de front, c’est bien une discrétisation du front, un ensemble de points de coordonnées X et Y avec une troisième dimension Z l’intensité, qui est en fait est la ddm en chaque point ou l’angle de phase du point (l’écart avec la surface en phase).

Vous proposez de faire une décomposition, une analyse zernike de l’image pour retrouver la PSF?

[B4lbu]

Et comment obtenez-vous w si ce n'est par un polynôme de Zernicke ?

C'est le logiciel qui le fait pour lui, donc j'imagine que cette information lui est totalement inutile

je crois qu'il confond analyse de Fourier d'une image et diffraction de Fraunhofer, c'est nouveau c'est "l'optique physique"

[Choc mou]

C'est le logiciel qui le fait pour lui, donc j'imagine que cette information lui est totalement inutile

je crois qu'il confond analyse de Fourier d'une image et diffraction de Fraunhofer, c'est nouveau c'est "l'optique physique"

Une fois de plus @B4lbu mis à part caricaturer pour le moment vous ne faites rien, vous ne produisez rien et ne répondez pas aux questions posées.
Faut pas sortir de polytechnique pour comprendre que je suis parti d’une simulation simple comme exemple de départ pour créer l’image du front de coma pure, car justement tout le monde le connaît bien.
Mais ce pourrait être un front bien plus compliqué par exemple issu d’une tavelure obtenue par je ne sais qu’elle méthode d’analyse, le problème resterai alors le même:

à partir d’une image front-d’onde donnée (objet 3D), comment retrouver sa psf en utilisant fft2?


Si pour vous c’est impossible dites-le, ou alors dites que vous ne savez pas le faire, mais SVP sortez si c’est uniquement pour polluer le débat. Par contre si vous pouvez faire avancer le sujet alors je serais heureux de vous lire.

[Choc mou]

Manifestement le 2 pi est déjà incorporé (les valeurs vont de -5,4 à +5,4

Voilà ce qu'on obtient à partir des données du fichier phase.fit

Pièce jointe 435406

«Manifestement le 2 pi est déjà incorporé (les valeurs vont de -5,4 à +5,4»

Oui effectivement dans cette version le 2pi est déjà incorporé, donc c’est l’image en angle de phase et non en ddm.
-5,457 à +5,457 = 1,737 ondes de PTV
C’est bien la déformation de départ de la simulation.


Votre image résultat se rapproche de ce que l’on devrait obtenir …
Comment avez-vous obtenu ce résultat SVP?

[gts2]

Comment avez-vous obtenu ce résultat SVP?

Utilisation de Mathematica (parce que je l'avais sous la main, Python, Matlab ... peut convenir)
récupération des données de phase sous forme d'une matrice
mat1 = Import["...phase.fit", {"Data", 1}];

récupération de la taille
{nRow, nCol} = Dimensions[mat1]

construction du front d'onde exp(j \phi)
d = Table[Exp[I*mat1[[i]][[j]]], {i, nRow}, {j, nCol}];

transformée de Fourier
fw = Fourier[d];

Norme et élévation au carré
abs = Abs[fw]; PSF = abs^2;

Des bricoles pour régler le problème de présentation de FFT avec le zéro au cen
hshift = IntegerPart[(nRow + .5)/2];
wshift = IntegerPart[(nCol + .5)/2];
fourierimage=Transpose[RotateLeft[ Transpose[RotateLeft[PSF, hshift]], wshift]];

transformation en image (le /20 est un peu au pif pour ajuster)
Image[fourierimage/20]

[Choc mou]

Utilisation de Mathematica (parce que je l'avais sous la main, Python, Matlab ... peut convenir)
récupération des données de phase sous forme d'une matrice
mat1 = Import["...phase.fit", {"Data", 1}];

récupération de la taille
{nRow, nCol} = Dimensions[mat1]

construction du front d'onde exp(j \phi)
d = Table[Exp[I*mat1[[i]][[j]]], {i, nRow}, {j, nCol}];

transformée de Fourier
fw = Fourier[d];

Norme et élévation au carré
abs = Abs[fw]; PSF = abs^2;

Des bricoles pour régler le problème de présentation de FFT avec le zéro au cen
hshift = IntegerPart[(nRow + .5)/2];
wshift = IntegerPart[(nCol + .5)/2];
fourierimage=Transpose[RotateLeft[ Transpose[RotateLeft[PSF, hshift]], wshift]];

transformation en image (le /20 est un peu au pif pour ajuster)
Image[fourierimage/20]

Merci gts2, je vais regarder cela de plus près.

[gts2]

Pourquoi faut-il obligatoirement passer par le calcul des coefficients de Zernike ?

Cela n'a rien d'obligatoire, mais comme vous donniez un exemple simple, j'avais supposé que vous l'aviez obtenu par simulation.

Vous proposez de faire une décomposition, une analyse Zernike de l’image pour retrouver la PSF?

Je ne propose rien du tout, mais si les données ne sont pas une simulation, d'où viennent les données du front d'onde ?
A priori, celles-ci ne sont pas connues, ce que l'on connait c'est l'image finale.

[Choc mou]

J’ai trouvé une solution.

@gts2 ton développement m’a inspiré … super merci.

En fait après une petite recherche je suis tombé sur les bases élémentaires d’optique (bien faibles par rapport aux multi-super-connaissances d’ @B4lbu).

A.exp(iw ) = est l’écriture en complexe du front-d’onde w où A est l’amplitude et i² = -1
et en clair exp(iw ) est cos(phi) + i sin(phi) où (phi) est l’angle de phase.

Donc A. exp(iw) = A[cos(phi) + i sin(phi)]

Comme l’image du front est exprimé en angle de phase (phi) il suffit d’en calculer le cosinus et le sinus.
J’ai donc transformé l’image du front en un tableau de valeurs à 3 colonnes (X, Y, phi), phi est l’intensité du pixel déjà à l’échelle.
N’étant pas fort en programmation j’ai juste utilisé le tableur Excel pour calculer
(phi) => cos(phi)
(phi) => sin(phi)
puis j’ai créé 2 tableaux, l’un (X, Y, cos(phi)) et l’autre (X, Y, cos(phi))
Et enfin en important ces 2 tableaux cela me donne 2 images nommées cos(phi) et sin(phi)

Petit détail*:
comme sin(0) = 0 il n’y à pas de problème
mais cos(0) = 1, le fond du cadre à zéro se rempli de 1. Il faut donc multiplier cette image par l’image de la pupille (des 1 dans la pupille et des 0 hors de la pupille) pour retrouver le fond de l’image à zéro sans modifier les pixels à l’intérieur de la pupille.

La formule calculant la PSF en fonction du front-d’onde étant:

PSF = | TF-1{pup.exp(iw)} |²

il suffit de faire la transformée inverse du couple d’images (cos; sin) pour retrouver la PSF (power ou fréquence au carré). Comme quoi une TF inverse nécessitant 2 images dans ce cas est bien différente d’une TF directe qui n’a besoin que d’une image.

Voici le résultat en image:
PS lors de la conversion tableau en image j’ai du multiplier les valeurs par 30000 car mon soft de transformation ne fonctionne qu’en nombre entier (16bits de -32768 à +32767) pour pouvoir garder au moins 4 décimales significatives des cos et sin (décimales compris entre -1 et 1).
Et les TF sont indépendantes d’intensités proportionnelles.

D’abord les images cos et sin en .fit Cos-Sin.zip

Et la capture d’écran
Cap_fft2.jpg


Est-ce que de votre coté vous obtenez le même résultat car je pense que cela dépend des soft de FFT?

[gts2]

Petit détail*:
comme sin(0) = 0 il n’y à pas de problème
mais cos(0) = 1, le fond du cadre à zéro se rempli de 1.

Oui j'avais oublié ce "détail", donc compléter mon message précédent par :
mat2 = Import["...pupille.fit", {"Data", 1}];
et d = mat2*d; avant Fourier.

Comme quoi une TF inverse nécessitant 2 images dans ce cas est bien différente d’une TF directe qui n’a besoin que d’une image.

Ce n'est pas directement lié à TF et TF-1, mais plutôt au fait que les données usuelles sont réelles.

Est-ce que de votre coté vous obtenez le même résultat car je pense que cela dépend des soft de FFT ?

Cela me donne bien le même résultat, je ne suis pas spécialiste des différents softs, mais cela devrait donner la même chose, les nuances se faisant sur les préfacteurs devant l'intégrale, raisonnement en fréquence ou pulsation ...

[Choc mou]

Cela me donne bien le même résultat, ...

Donc cela fonctionne aussi chez vous, Super ...

Bon après il faut que je retrouve la FTO décomposée en FTM et FTP.

[Choc mou]

La FTO est la TF de la PSF.

Veuillez me dire SVP qu'elle image dans le carré de droite est la FTM et celle de FTP ?
Vous verrez à gauche le min et max de chaque image.


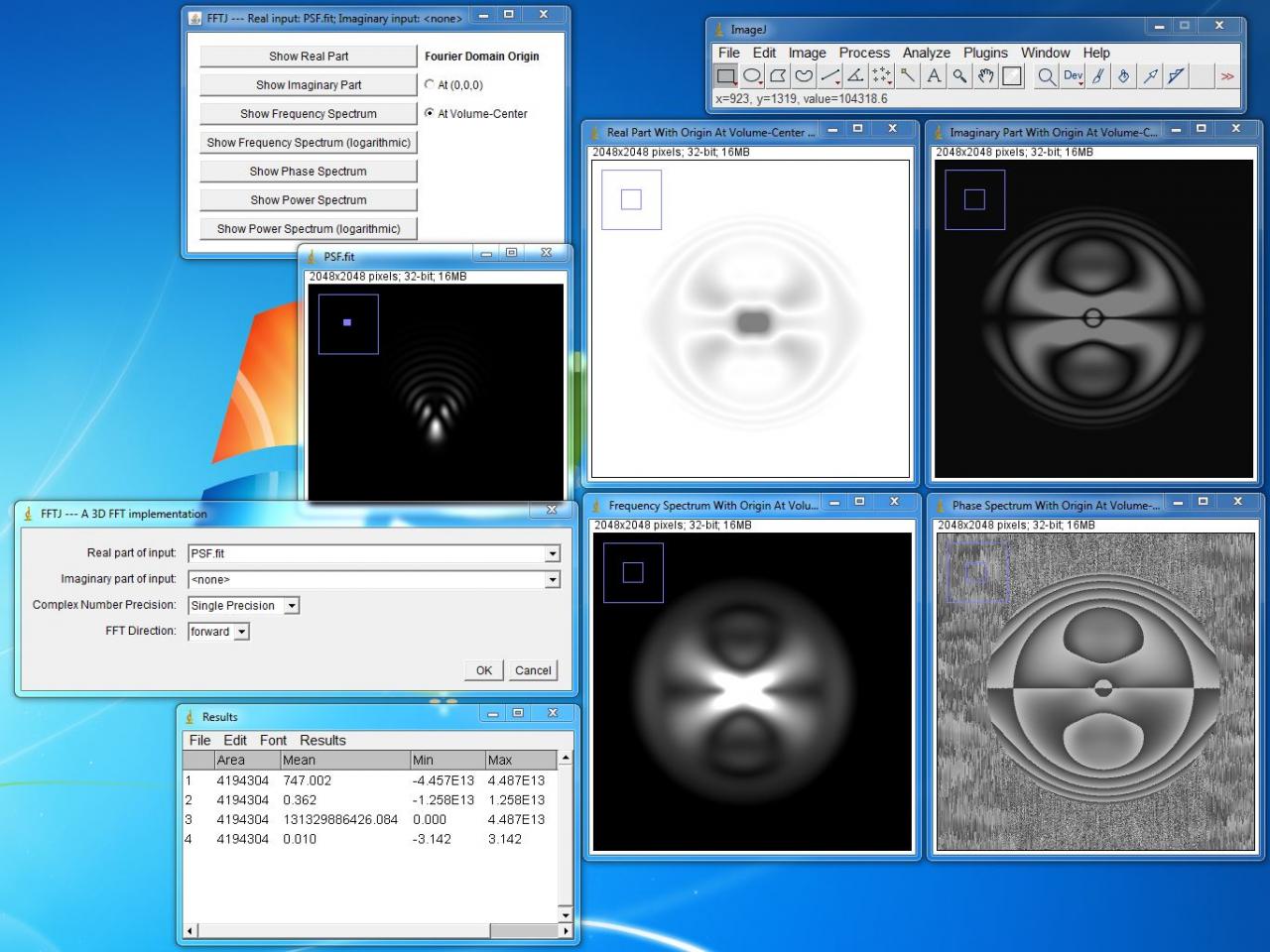
Après pour partir de l'image front-d'onde c'est quoi l'autocorrélation de l'image ? (convolution par elle même ?)

[gts2]

Bonjour,

Pour ce qui est de l'autocorrélation voir univ-grenoble-alpes.fr, la page 4 suffit.

Pour ce qui est de FTM et TFP, c'est marqué en toutes lettres dans le titre (en bas à droite) : "Phase spectrum" donc FTP (P est pour phase, donc arg())
en bas à gauche, c'est moins net, mais par élimination ... FTM (M c'est pour modulation ou module (donc abs())

[invite18230371]

vous pouvez calculer des fft sur images assez simplement sur matlab ou scilab (open source), fonction fft2, tout en maitrisant l'ensemble des étapes de calcul

Exactement,
Par exemple, sous matlab faire la fft2 de l'image de la pupille que vous montrez ne marchera pas !!!
Regarder du coté de la fonction fftshift, et ifftshift qui permet de mettre l'origine de l'image dans la convention utilisé par matlab...

Juste une idée...

Quel est votre language de programmation ? Peut-on voir le script ?

[Choc mou]

Bonjour,

Pour ce qui est de l'autocorrélation voir univ-grenoble-alpes.fr, la page 4 suffit.

Pour ce qui est de FTM et TFP, c'est marqué en toutes lettres dans le titre (en bas à droite) : "Phase spectrum" donc FTP (P est pour phase, donc arg())
en bas à gauche, c'est moins net, mais par élimination ... FTM (M c'est pour modulation ou module (donc abs())

J’ai posé la question sur la FTM et la FTP (module de la Fonction de Transfert Optique et sa phase) car selon mes logiciels ont à que le couples suivant:
- (réel ; imaginaire)
- (fréquence ; phase)
- (module ; argument)
Donc si on se fie aux mots la FTModule et la FTPhase serait dans 2 couples différents.

Voici ici la version Module et Argument:


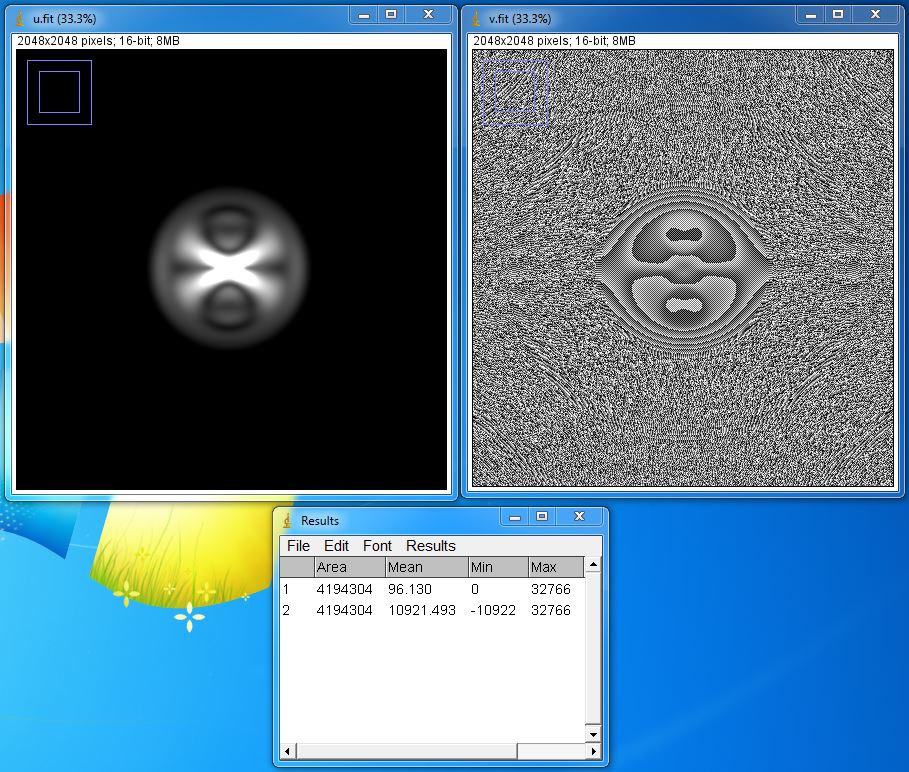
On observe bien que
- Fréquecy Spectrum du couple précédant (fréquence ; phase) ressemble beaucoup au Module du couple (module ; argument)
- mais que Phase Spectrum du couple (fréquence ; phase) est différent surtout en partie centrale de l’argument du couple (module ; argument).
C’est pourquoi j’ai des doutes sur l’image FTP. A votre avis ?

Merci pour votre lien sur l’autocorrelation, je regarderai cela avec précision ce soir.

[Choc mou]

Quel est votre language de programmation ? Peut-on voir le script ?

Je ne dispose pas de Matlab
Pour répondre à votre question le script est présenté dans mon post d'hier de 18h56

[gts2]

- (réel ; imaginaire)
- (fréquence ; phase)
- (module ; argument)
Donc si on se fie aux mots la FTModule et la FTPhase serait dans 2 couples différents.

C'est pas très clair : un complexe peut se décomposer de deux manières : (réelle, imaginaire) ou (norme/module, argument/phase)

Je ne vois pas ce qu'est la fréquence : si on est dans l'espace "géométrique" les coordonnées du graphe sont (x,y), si on dans l'espace de Fourier les coordonnées du graphe sont les fréquences (fx,fy).
Quel est le logiciel, avez-vous un lien sur le mode d'emploi pour comprendre ces trois représentations.

[Choc mou]

C'est pas très clair : un complexe peut se décomposer de deux manières : (réelle, imaginaire) ou (norme/module, argument/phase)

Je ne vois pas ce qu'est la fréquence : si on est dans l'espace "géométrique" les coordonnées du graphe sont (x,y), si on dans l'espace de Fourier les coordonnées du graphe sont les fréquences (fx,fy).
Quel est le logiciel, avez-vous un lien sur le mode d'emploi pour comprendre ces trois représentations.

« C’est pas très clair … »
De ce coté là je ne peux que vous faire confiance ...

Il y a beaucoup de logiciels libres qui permettent de faire des FFT surtout pour filtrer des images.
Mais peu permettent de réaliser des FFT inverses.
Perso j’en utilise deux, ImageJ avec un de ses plugins FFTJ et IRIS d’Astrosurf

Image J:
https://imagej.nih.gov/ij/index.html

dans le descriptif FFTJ vous trouverez les différents type de résultats possibles
https://sites.google.com/site/piotrw...e/parallelfftj

Dans la capture d’écran vous retrouvez bien les 2 couples
(1_réel ; 2_imaginaire) et (3_fréquence ; 4_phase) que l’on retrouve dans les entêtes des images.
PS: seul le couple (1_réel ; 2_imaginaire) permet de retrouver l’imge d’origine après FFT par FFT inverse.
Cap_FTOa.jpg

IRIS:
http://www.astrosurf.com/buil/iris-software.html

et ses fonction fftd et ffti
Cap_fftd-ffti.JPG

Qui par abut de langage ou de traduction dans l’aide pourait être le couple (module ; phase).

[gts2]

dans le descriptif FFTJ ... Dans la capture d’écran vous retrouvez bien les 2 couples
(1_réel ; 2_imaginaire) et (3_fréquence ; 4_phase)

Qui n'a pas grand sens : dans les quatre graphes, les axes sont les fréquences spatiales, les quatre graphes, si on raisonne en coordonnées, sont tous des graphes fréquentiels, et on représente soit (Re,Im) soit (module,argument).

Pour ce qui est de argument vs. phase, argument se réfère au nombre complexe au point (i,j) et phase se réfère à l'interprétation qu'on en fait comment étant la phase de l'onde de fréquence (fx,fy).

Le vocabulaire d'Iris est plus cohérent.

[Choc mou]

Je suis désolé, mais je n'ai pas pu comprendre et je ne suis pas arrivé à obtenir la Fonction de Transfert Optique (FTO) à partir du front-d'onde sans passer par la PSF.
Si vous pouviez m'aider SVP ...

[Choc mou]

Sans nouvelles ces jours-ci, voici un document du Net qui pourrait aider à définir la méthode à déterminer
Speckles.pdf

[Choc mou]

J'ai trouvé un plugin d' ImageJ créé par l'Université Nationale de Colombie qui traite de l'optique
https://unal-optodigital.github.io/N...alPropagation/

Il suffit de placer le Dowload.zip (OD) décompressé dans le dossier Plugin d'ImageJ pour retrouvé cet outil qui semble particulièrement utile.
Pourriez-vous m'aider et comprendre son fonctionnement ?


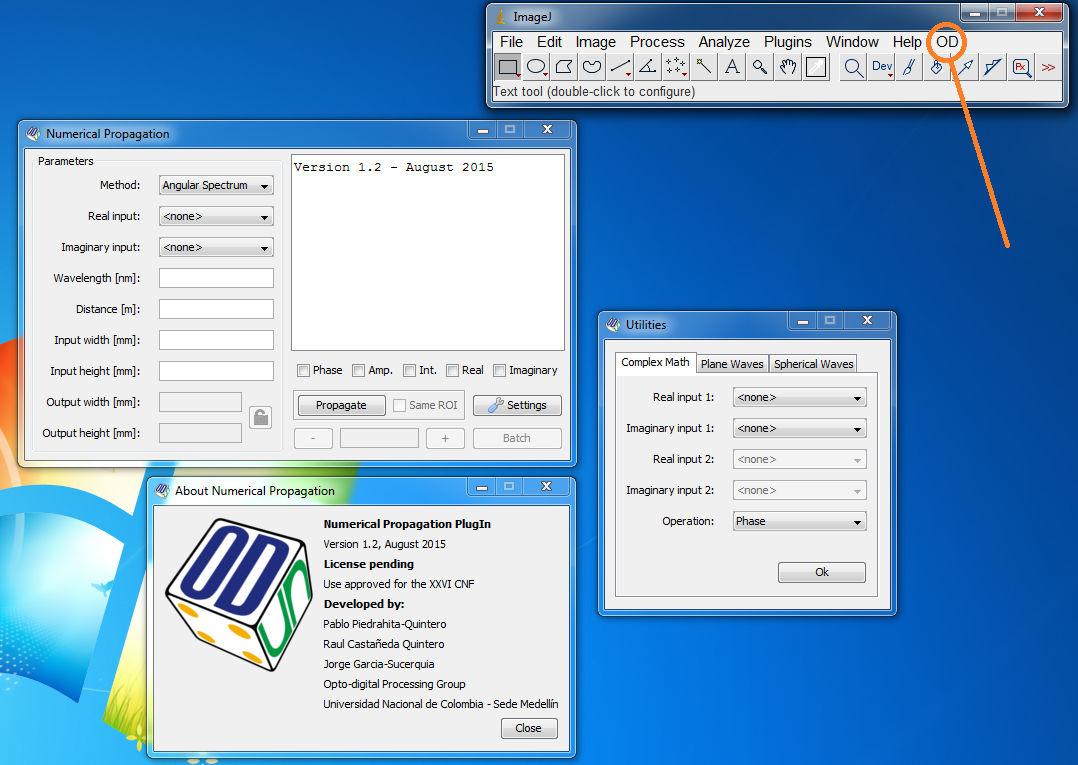
@gts2

[Paraboloide_Hyperbolique]

Pourriez-vous m'aider et comprendre son fonctionnement ?

A priori, personne ici ne connaît cet outil, sauf coup de chance. Avez-vous eu le réflexe "RTFM" ?

https://ciencias.medellin.unal.edu.c...anual_v1.2.pdf

[Choc mou]

Désolé je n'ai pas eu le reflex "RTFM" qui devrait-être systématique
Merci je vais rentrer dedans ...