Optique physique FFT 2D

[Choc mou]

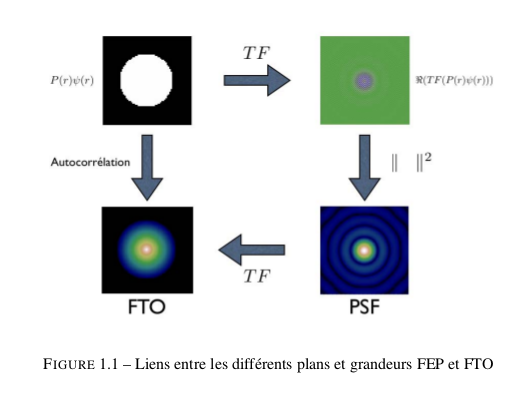
Dans toutes les publications comme les thèses d’astronomie jusqu’à la microscopie, on retrouve les formules qui relient le front-d’onde à la fonction d’étalement du point (PSF) en passant par la fonction de transfert optique qui caractérise l’instrument.

Les publications résument souvent les liens entre ces 3 notions comme dans le tableau suivant*:

ant-1.png

Le front-d’onde, la PSF et la FTO sont liées par des formules basées sur les transformations de Fourier souvent compliquées pour moi.
Cependant j’ai des notions de base et il est facile d’utiliser des logiciels de FFT (Fast Fourier Transform).
La FFT d’une image produit 2 images (réel et imaginaire) ou (fréquence et phase). La transformée inverse de son coté nécessite 2 images en entrée.

Alors je sollicite votre aide pas pour reéxprimer les formules mathématiques, mais de me montrer la procédure par application de FFT 2D sur images sur la base d’un exemple explicite. Je ne souhaite pas partir du front d’onde plat qui produit la bien connue PSF théorique optimale, mais d’un front-d’onde déformé.

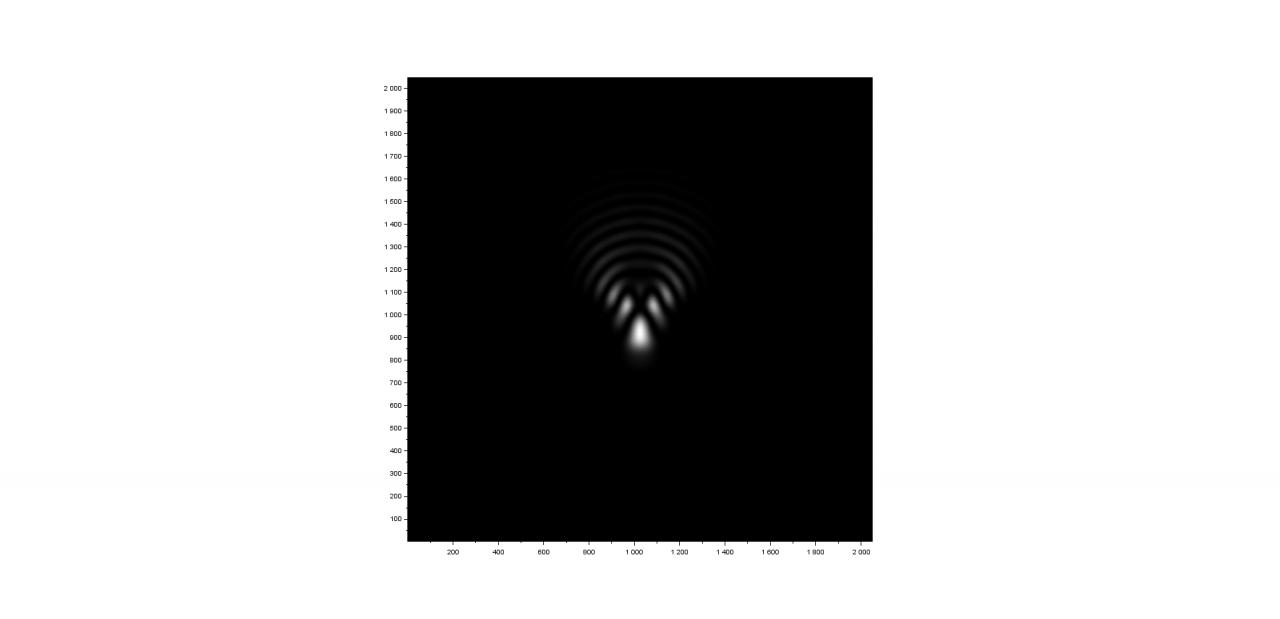
Je ne veux pas non plus un front d’onde trop complexe qui produit une PSF tavelure (speckle) dont on ne peut pas vérifier la correspondance des résultats, mais d’un front d’onde connu comme par exemple l’image du front-d’onde de coma pure qui produit une PSF classique bien connue et dissymétrique.
Je propose de partir de l’image front-d’onde avec la donnée du PTV (Peak To Valley) d’environ 1,5 ondes (voir exemple ci-après).

WR.PNG

phi.png

En résumé comment en partant de l’image front-d’onde ci-après retrouver l’image de sa PSF, ainsi que celle de sa FTO (module FTM et phase FTP)*?
Et comment retrouver cette même FTO en partant de l’image PSF trouvée précédemment*?

C'est un cas d'école
-----

[Paraboloide_Hyperbolique]

Bonjour,

J'ai bien lu que vous ne demandez pas de math. Cependant, il me semble impossible d'expliquer et traiter votre problème sans. Donc, voici:

Soit le signal/l'image observé, la fonction d'étalement du point et le signal/l'image qui, convoluée avec la psf, donne le signal observé.

Mathématiquement cela se note:



où désigne l'opération de convolution.

Un problème classique, consiste à retrouver à partir du signal observé et de la . Le fait de retrouver s'appelle une déconvolution. Dans la littérature, il y a des milliers de techniques différentes pour effectuer cela.

Pour effectuer une déconvolution "naïve*", on peut passer dans le domaine de Fourier et ré-exprimer le problème sous la forme:



où désigna la transformée de Fourier et l'opération désigne la multiplication composante par composante (on peut démontrer que l'opération de convolution correspond à l'opération de multiplication dans le domaine de Fourier).

est simplement la FTO. En pratique, on "agrandit" la psf en ajoutant des zéros (zero-padding) pour faire correspondre sa taille à la taille du signal .


A partir de la formule ci-dessus, il est alors (en principe) possible de retrouver la via:



et bien sûr:



où est la transformée de Fourier inverse désigne la partie réelle et la division est effectuée composante par composante.


*"naïve", car cela fonctionne dans un cas idéal (signaux/images parfaites sans bruit). En pratique la procédure décrite ci-dessus est très sensible en présence de bruit et donne rapidement de mauvais résultats. Il faut alors procéder à une opération dite de régularisation. Une méthode de régularisation basique qui généralise les formules ci-dessus est la déconvolution de Wiener. Celle-ci est moins sensible a bruit, au prix de l'ajout d'un certain "flou" dans les signaux/images reconstruits.

[86cat]

Bonjour

Je n'ai pas compris grand'chose. J'ai juste envie d'écrire ceci:
Dans les problèmes d'optique, on s'intéresse beaucoup "à la lumière". Ce qu'elle est. Comment elle se propage. Sa vitesse. Les interférences qu'elle produit... Que sais-je.
Mais nous n'avons pas "accès" à la lumière. Nous n'avons accès qu'à ses effets. Modification de l'opacité du chlorure d'argent, réaction des cellules photosensibles de notre rétine, expulsions d'électron de la surface d'un métal (effet photoélectrique)...
Voilà.
Cà peut peut être aider à votre réflexion sans formules mathématiques........

86cat

[Choc mou]

Oui merci "Paraboloide_Hyperbolique" pour m'avoir aimablement répondu, et sous une forme particulièrement lisible.
En fait j'avais bien compris tout cela, mais sur le plan pratique avec mes softs de FFT cela ne fonctionne pas (il doit bien y avoir une raison, type de FFT peut-être ? ... )
C'est pour cela que je souhaite SVP un exemple pratique en images pour comprendre les étapes et là où il y a un loup de mon coté
Départ image du front-d'onde déformé, vers sa PSF et vers sa FTO. Puis PSF vers FTO (FTM + FTP) pour retrouver normalement les mêmes images FTO (FTM + FTP) obtenues à partir du front-d'onde initial.

[A voir en vidéo sur Futura]

[gts2]

Bonjour,

Est-ce vous pourriez fournir un fichier correspondant à votre front d'onde (parce que là avec un copier-coller on n'a que la norme) ou l'expression (norme,argument) de votre front d'onde ?

[Choc mou]

Merci gts2 de rentrer dans le sujet.
voici l'image de la pupille et l'image du front-d'onde exprimé en 2(pi)lambda = angle de phase : Pj.zip
Les images font 2048x2048 pixels
Si on veut exprimer le front en valeur d'onde il suffit de diviser l'image par 2(pi) soit environ 6,28
Il y a des pixels en avance de phase (valeur positive) et des pixels en retard de phase (valeur négative). Le font est à zéro.
Pour la pupille, dedans on est à 1 et en dehors on est à zéro.

[Choc mou]

J'ajoute que les images sont en 32 bits avec des valeurs décimales

[Paraboloide_Hyperbolique]

J'ai rapidement jeté un coup d'oeil aux images. Simple question: est-il normal que l'image de la pupille fasse 2048 x 2048 pixels, tandis que celle du front d'onde soit de 2024 x 2024 ?

[Choc mou]

Paraboloide_Hyperbolique, Non ce n'est pas normal.
Je suis aller trop vite.
Les images de préférence doivent être une puissance de 2 (32,64,128,512,1024,2048, ...)
Alors j'ai refais la pièce jointe : PJ_mod.zip

Veuillez m'excuser pour cette erreur.

[B4lbu]

Bonjour,
Si je comprends, vous voulez recalculer la phase en plan pupille à partir de la PSF? Ce n'est pas possible puisque les détecteurs sont sensibles à l'intensité lumineuse, pas à l'amplitude, ce qui explique la présence du module au carré dans le calcul de la PSF, qui mène à perdre l'information sur la phase. Pour faire ce que vous voulez faire, il faut utiliser des algorithmes de reconstruction de phase :
https://en.wikipedia.org/wiki/Phase_retrieval

[Choc mou]

Bonjour,
Si je comprends, vous voulez recalculer la phase en plan pupille à partir de la PSF? Ce n'est pas possible puisque les détecteurs sont sensibles à l'intensité lumineuse, pas à l'amplitude, ce qui explique la présence du module au carré dans le calcul de la PSF, qui mène à perdre l'information sur la phase. Pour faire ce que vous voulez faire, il faut utiliser des algorithmes de reconstruction de phase :
https://en.wikipedia.org/wiki/Phase_retrieval

Non B4lbu on en est pas là. au contraire partir du front-d'onde et construire la PSF et la Fonction de transfert ...
Comme comme je l'ai écrit plus haut :
"Départ image du front-d'onde déformé, vers sa PSF et vers sa FTO. Puis PSF vers FTO (FTM + FTP) pour retrouver normalement les mêmes images FTO (FTM + FTP) obtenues à partir du front-d'onde initial."

comme dans le tableau initial :

[B4lbu]

Alors je ne comprends pas le problème, c'est que vous ne trouvez pas le même résultat entre l'autocorrélation du plan pupille et la TF inverse du module au carré de sa TF ? Déjà avec un front d'onde plan est ce que vous obtenez bien la tache d'Airy?

[Choc mou]

Il n’y a aucun problème avec un front plat pour obtenir le disque d’Airy puisque qu’il n’y a pas de différence de marche.

Par contre pour un front d’onde déformé ce n’ai pas aussi simple.
Primo, contrairement a ce qui est annoncer trop souvent dans la littérature, la relation qui relie le front et la PSF n’est pas
PSF = module au carré de {TF[pup.exp(iw)]}
mais
PSF = module au carré de {TF-1[pup.exp(iw)]}
donc à partir de l’image front-d’onde, la PSF ne s’obtient par pas par une transformée de Fourier direct mais par une transformée de Fourier inverse ce qui différent et nécessite 2 images en entrée.

Secundo pour le calcul de la Fonction de Transfert Optique:
FTO = autocorrelation du front-d’onde.
l’autocorrelation du front-d’onde c’est quoi? La convolution de l’image front par elle même ou la TF [TF(Front-d’onde)]?
Dans ces 2 cas comment faire, puisque qu’on vient de voir qu’un front serait constituer de 2 images[pup.exp(iw)] ?

Tertio, pour la FTO à partir de l’image de PSF
FTO = TF(PSF) cela est soit disant simple
Comme l’image de la PSF est réelle positive, TF(PSF) génère 2 images, soit le couple (module; argument) ou soit le couple (fréquence; phase). Laquelle est la FTM et laquelle est la FTP?

Voilà c’est pourquoi je demande de partir du cas d’école simple, de partir de l’image du front-d’onde d’une coma pure, dans laquelle chaque pixel à pour intensité l’équivalent de la différence de marche en ce point, soit exprimé en valeur onde ou soit exprimé en angle de déphasage (via la constante 2pi).
C’est pourquoi je remet ici le zip de l’image de la pupille pup et de l’image du front-d’onde en 32bits. Dans cet exemple le PTV est d’environ 1,7 ondes
PJ_mod.zip

Je rappel que le résultat de la PSF à trouver doit ressembler au résultat suivant que l’on retrouve partout dans toute les littératures
WR.PNG

PS: Les formules mathématiques dans une physique théorique c’est parfait, mais seule l’expérience pratique est révélatrice, … et là je sollicite le traitement d’un cas d’école simple en image pour comprendre.

[gts2]

la PSF ne s’obtient par pas par une transformée de Fourier direct mais par une transformée de Fourier inverse ce qui différent et nécessite 2 images en entrée.

TF ou TF-1 c'est kif-kif, il y a juste un signe, (mais il faut y faire attention certes), donc si TF-1 nécessite deux images (je suppose intensité, phase), la TF c'est idem.

[B4lbu]

l’autocorrelation du front-d’onde c’est quoi?

c'est l'autocorrélation du champ complexe en plan pupille, je ne vois pas comment l'expliquer autrement

TF(PSF) génère 2 images, soit le couple (module; argument) ou soit le couple (fréquence; phase). Laquelle est la FTM et laquelle est la FTP?

génère un champ complexe, que vous pouvez exprimer en sa partie réelle et sa partie imaginaire, ou son module et son argument ou ... tout cela n'étant que des représentations différentes du même champ complexe

La FTM est le module de la FTO, la FEP est la traduction française de la PSF

Voilà c’est pourquoi je demande de partir du cas d’école simple, de partir de l’image du front-d’onde d’une coma pure, [...] Je rappel que le résultat de la PSF à trouver doit ressembler au résultat suivant que l’on retrouve partout dans toute les littératures

Tout a fait plusieurs personnes ici savent faire, mais apparemment c'est vous qui n'arrivez pas à faire le calcul, il va donc falloir expliquer où ça coince (donc poser sur le papier les calculs que vous faites) pour espérer qu'on puisse vous débloquer

PS: Les formules mathématiques dans une physique théorique c’est parfait, mais seule l’expérience pratique est révélatrice

Pour interpréter correctement les équations, il n'y a pas le choix il faut à un moment ou un autre se pencher sur le déroulement qui arrive au résultat

[Choc mou]

TF ou TF-1 c'est kif-kif, il y a juste un signe, (mais il faut y faire attention certes), donc si TF-1 nécessite deux images (je suppose intensité, phase), la TF c'est idem.

Pour moi c'est peut-être l'équivalent pour une image sans phase, mais pas pour un front-d'onde déformé.
En tous les cas lorsqu'on qu'on regarde les 2 résultats au centre de l'image on voit bien que les TF sont loin du résultat recherché de droite

[Choc mou]

c'est l'autocorrélation du champ complexe en plan pupille, je ne vois pas comment l'expliquer autrement


génère un champ complexe, que vous pouvez exprimer en sa partie réelle et sa partie imaginaire, ou son module et son argument ou ... tout cela n'étant que des représentations différentes du même champ complexe

La FTM est le module de la FTO, la FEP est la traduction française de la PSF



Tout a fait plusieurs personnes ici savent faire, mais apparemment c'est vous qui n'arrivez pas à faire le calcul, il va donc falloir expliquer où ça coince (donc poser sur le papier les calculs que vous faites) pour espérer qu'on puisse vous débloquer


Pour interpréter correctement les équations, il n'y a pas le choix il faut à un moment ou un autre se pencher sur le déroulement qui arrive au résultat

Interpréter correctement les équations c'est bien à condition d'obtenir le bon résultat en image.
PS : Les images sources sont disponibles pour test et logiquement par TF sur images on doit y arriver.

[Choc mou]

"c'est l'autocorrélation du champ complexe en plan pupille, je ne vois pas comment l'expliquer autrement"

Ok mais cela donne quoi comme images sur l'exemple ?

[B4lbu]

Ok mais cela donne quoi comme images sur l'exemple ?

Je ne sais pas, puisque je ne sais pas les calculs que vous avez fait pour afficher ces images

Par contre, si vous calculez la FFT de la phase affichée à gauche, il faut rajouter pas mal de zero padding autour de la pupille pour ne pas que le fenêtrage bruite le résultat de la FFT

[gts2]

Pour moi c'est peut-être l'équivalent pour une image sans phase, mais pas pour un front-d'onde déformé.
En tous les cas lorsqu'on qu'on regarde les 2 résultats au centre de l'image on voit bien que les TF sont loin du résultat recherché de droite.

TF^-1(f(x,y))=TF(f(-x,-y)) à des pb de normalisation près.

Donc il y a des problèmes mais pas dus à la confusion TF, TF^-1

[Choc mou]

Je ne sais pas, puisque je ne sais pas les calculs que vous avez fait pour afficher ces images

Par contre, si vous calculez la FFT de la phase affichée à gauche, il faut rajouter pas mal de zero padding autour de la pupille pour ne pas que le fenêtrage bruite le résultat de la FFT

Quand vous utilisez une voiture vous n'expliquez pas la thermodynamique de ce qui se passe dans le moteur, vous la conduisez simplement probablement en respectant le code de la route
Donc pour le calcul j'utilise les softs de FFT sur images

"il faut rajouter pas mal de zero padding autour de la pupille pour ne pas que le fenêtrage bruite le résultat de la FFT"
Si vous ouvrez les images transmises depuis le début vous verrez que ce soit la pupille ou le front, la plage utile fait 256x256 pixels et que les images font 2048x2048 pixels. Donc le "padding" est largement suffisant pour une psf résultat bien dessinée.
Sans rentrer dans les images nous n'arriverons à rien.

[Choc mou]

TF^-1(f(x,y))=TF(f(-x,-y)) à des pb de normalisation près.

Donc il y a des problèmes mais pas dus à la confusion TF, TF^-1

Oui je pense aussi que cela ne provient d'une confusion TF ou TF-1(inverse).

[B4lbu]

Quand vous utilisez une voiture vous n'expliquez pas la thermodynamique de ce qui se passe dans le moteur, vous la conduisez simplement probablement en respectant le code de la route

sauf que là vous nous demandez pourquoi vous avez eu un accident, sans nous expliquer à quel moment vous n'avez pas respecté le code de la route

Donc pour le calcul j'utilise les softs de FFT sur images

ça se précise, est ce que vous maitrisez les calculs qui y sont faits? pour information au cas où, vous pouvez calculer des fft sur images assez simplement sur matlab ou scilab (open source), fonction fft2, tout en maitrisant l'ensemble des étapes de calcul

Sans rentrer dans les images nous n'arriverons à rien.

l'aberration de coma et le calcul théorique sont exacts, donc c'est uniquement dans votre implémentation qu'il y a une erreur, mais puisque vous n'y mettez pas du votre pour formaliser votre problème, je ne vais pas le faire à votre place

[Choc mou]

sauf que là vous nous demandez pourquoi vous avez eu un accident, sans nous expliquer à quel moment vous n'avez pas respecté le code de la route


ça se précise, est ce que vous maitrisez les calculs qui y sont faits? pour information au cas où, vous pouvez calculer des fft sur images assez simplement sur matlab ou scilab (open source), fonction fft2, tout en maitrisant l'ensemble des étapes de calcul

l'aberration de coma et le calcul théorique sont exacts, donc c'est uniquement dans votre implémentation qu'il y a une erreur, mais puisque vous n'y mettez pas du votre pour formaliser votre problème, je ne vais pas le faire à votre place

B4lbu je croix au contraire que c’est vous qui n’avez rien lu ou compris au problème posé.
Chercher des excuses ou jouer au ping-pong n’ai pas constructif.
Cela m’étonnerait que de votre coté vous implémentiez matlab ou scilab opération réservée aux développeurs programmeurs.
Cela m’étonnerait beaucoup que vous sachiez modifier un programme de Fast Fourier Transform fft2 qui est le même dans presque tout les logiciels et ce depuis de nombreuses années.
Donc si vous rentrée une image, la fft2 de cette image sera la même dans tous les logiciels fft2.

Je pense au contraire que vous ne connaissez pas l’optique puisque vous reproduisez uniquement les formules trouvées dans les livres sans avoir fait une seule fft2 sur un front déformé.
Dit autrement vous ne savez pas transformée l’image du front-d’onde d’une simple coma pure classique pour que par fft2 (ou inverse fft2) on retrouve la psf et la FTO.

Vous ne m’avez pas révéler aussi ce qu’était l’autocorrelation d’une image dans ce cas, convolution ou fft2?

J’aime bien aussi votre manière de dire «puisque que vous avez un problème démerdez-vous ...»

Affirmer que le problème est pas ou mal posé est évidemment une contre vérité.
J’ai joint l’image du front-d’onde comme affiché dans tous les analyseurs front-d’onde avec son PTV exprimé en onde et l’image de la pupille. Ce sont bien les 2 données d’entrées nécessaire et suffisantes pour normalement retrouver la PSF par fft2 d’un front-d’onde comme présenter dans les formules.
Après comment modifier cette image d’entrée pour la convertir en image exp(iw) là est la question? Et ça c’est du pratique de l’optique physique.

Appuyer sur la touche fft2 cela tout le monde c’est le faire et sans accident possible.

[B4lbu]

Cela m’étonnerait que de votre coté vous implémentiez matlab ou scilab opération réservée aux développeurs programmeurs.
Cela m’étonnerait beaucoup que vous sachiez modifier un programme de Fast Fourier Transform fft2 qui est le même dans presque tout les logiciels et ce depuis de nombreuses années.
Donc si vous rentrée une image, la fft2 de cette image sera la même dans tous les logiciels fft2.

Je pense au contraire que vous ne connaissez pas l’optique puisque vous reproduisez uniquement les formules trouvées dans les livres sans avoir fait une seule fft2 sur un front déformé.
Dit autrement vous ne savez pas transformée l’image du front-d’onde d’une simple coma pure classique pour que par fft2 (ou inverse fft2) on retrouve la psf et la FTO.

Détrompez-vous, je vous joint le résultat (à un facteur d'échelle près, je ne manipule pas les formats .fit, c'était plus rapide de recalculer la phase à partir du polynôme de Zernike de coma) fait sur scilab en 5 min ...

Vous devez trouver à peu près le même résultat. Satisfait?

J’aime bien aussi votre manière de dire «puisque que vous avez un problème démerdez-vous ...»

je vous ai demandé d'exprimer clairement votre problème, maintenant vous refusez et êtes convaincu de déjà tout savoir, donc effectivement débrouillez vous

[Choc mou]

Détrompez-vous, je vous joint le résultat (à un facteur d'échelle près, je ne manipule pas les formats .fit, c'était plus rapide de recalculer la phase à partir du polynôme de Zernike de coma) fait sur scilab en 5 min ...

Vous devez trouver à peu près le même résultat. Satisfait?



je vous ai demandé d'exprimer clairement votre problème, maintenant vous refusez et êtes convaincu de déjà tout savoir, donc effectivement débrouillez vous

Pièce jointe 435395

En 5 minutes et bien Bravo.

De mon coté je ne sais rien, effectivement c'est pour cela que j'ai créé ce post.
Par contre vous n'êtes pas parti de l'image front-d'onde communiquée mais des polynômes de Zernike qui eux fonctionnent autrement.

[Choc mou]

Détrompez-vous, je vous joint le résultat (à un facteur d'échelle près, je ne manipule pas les formats .fit, c'était plus rapide de recalculer la phase à partir du polynôme de Zernike de coma) fait sur scilab en 5 min ...

Vous devez trouver à peu près le même résultat. Satisfait?



je vous ai demandé d'exprimer clairement votre problème, maintenant vous refusez et êtes convaincu de déjà tout savoir, donc effectivement débrouillez vous

Pièce jointe 435395

En fait vous avez pris le problème à l'envers, vous êtes partis du coef zernike de comma pour créer le front-d'onde et sa PSF. C'est donc fausser la donne.
Ensuite soit disant vous ne lisez pas le images.fit, hors matlab comme scilab peuvent certainement convertir ce type d'image en tableau ou comme bon nombre d'éditeur d'image lisent et convertissent ce format.

Pour la nième fois vous vous écrivez "je vous ai demandé d'exprimer clairement votre problème" et bien je l'ai fais n fois, dont la dernière :
"Affirmer que le problème est pas ou mal posé est évidemment une contre vérité.
J’ai joint l’image du front-d’onde comme affiché dans tous les analyseurs front-d’onde avec son PTV exprimé en onde et l’image de la pupille. Ce sont bien les 2 données d’entrées nécessaire et suffisantes pour normalement retrouver la PSF par fft2 d’un front-d’onde comme présenter dans les formules.
Après comment modifier cette image d’entrée pour la convertir en image exp(iw) là est la question? Et ça c’est du pratique de l’optique physique."

[gts2]

Je suis aussi reparti de Zernicke et cela marche (moins bien que @B4lbu mais bon ...).

Donc le problème est dans "J’ai joint l’image du front-d’onde comme affiché dans tous les analyseurs front-d’onde" : c'est un affichage, le tout est de savoir comment cela est codé (relation phase niveau du pixel), c'est peut-être là qu'il y a un problème.

[Choc mou]

Je suis aussi reparti de Zernicke et cela marche (moins bien que @B4lbu mais bon ...).

Donc le problème est dans "J’ai joint l’image du front-d’onde comme affiché dans tous les analyseurs front-d’onde" : c'est un affichage, le tout est de savoir comment cela est codé (relation phase niveau du pixel), c'est peut-être là qu'il y a un problème.

«Je suis aussi reparti de Zernike et cela marche»
Bien sûr que cela fonctionne c’est exactement ce que j’avais déjà affiché dans les premières lignes de cette nouvelle discussion avec la capture écran de l’analyseur WinRoddier où le Zernike Z(3,-1) est à 150nm.
C’était le fichier WR.png que je re-affiche ici*:

WR.jpg

Donc @B4lbu n’a rien fait avancer d’un iota, au contraire il arrive au point de départ.
Je rappelle tout de même ici que la formule qui donne la PSF en fonction d’un front déformé dans la littérature est:

PSF = |TF{pup.exp(iw)}|² avec i² = -1
et donc par transformée de Fourier la fonction fft2 (et non par les zernikes) on devrait retrouver l’image de la PSF et la FTO (FTM et FTP)


«"J’ai joint l’image du front-d’onde comme affiché dans tous les analyseurs front-d’onde" : c'est un affichage, le tout est de savoir comment cela est codé (relation phase niveau du pixel)"»

Je suppose que vous avez tous reconnu que c’était bien l’image d’un front-d’onde de coma pure et comme je l’avais aussi déjà bien précisé le fichier image.fit est simplement l’image du front où l’intensité des pixels correspond aux différences de marches exprimé en valeur onde
comme PTV = 1,73 lambda
1,73 / 2 = 0,865 donc l’intensité des pixels vont de -0,865 à +0,865 ondes, les négatifs en retard de marche et les positifs en avance de marche.
Les valeurs des pixels étant positifs et négatifs on ne peut pas utiliser un .jpg ou un .png, de plus les valeurs étant décimales l’image est forcément en 32bits.

J’avais aussi ajouter que pour passer en image d’angle de phase il suffit de multiplier l’image par 2pi = 6,283…
(ddm = 2pi delta / lambda)

Voici le profil seulement sur la zone du centre puisque tout est à zéro sur le reste de l’image 2048x 2048 pixels
coupe.JPG

[gts2]

PSF = |TF{pup.exp(iw)}|² avec i² = -1 et donc par transformée de Fourier la fonction fft2 (et non par les zernikes)

Et comment obtenez-vous w si ce n'est par un polynôme de Zernicke ?

Et donc, @B4lbu n'a pas tord, tant que vous ne nous aurez pas expliqué comment vous obtenez w (puisque ce n'est pas avec un polynôme de Zernicke), on ne pourra avancer d'un iota.