matrice d'inertie

[invite7e448ed9]

j'ai un petit souci de calcul de matrice d'inertie....
je souhaite calculer la matrice d'inertie de ce corps (les 2 pièces jaune et verte):


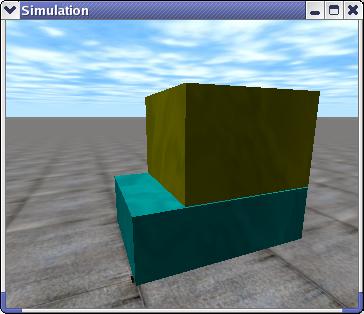
il s'agit donc de 2 parralélépipèdes, l'un sur l'autre, avec un léger décalage entre le deux selon l'axe horizontal

si je calcule le moment d'inertie pour un seul parrallélépipède, j'obtiens une matrice diagonale du type
a 0 0
0 b 0
0 0 c,
ce qui est ok, n'est-ce pas?

mais si je tente de faire le calcul pour les 2 parralélépipède ensemble, j'obtiens le même type de matrice diagonale, mais avec des valeurs différentes...
cela ne me semble par du tout normal..
qu'en pensez vous?

pour calculer mes matrices, je modélise mes corps au moyen d'une librairie C++, et le calcul sont fait tout seul, mais apparement je dois faire qqch de faux, car une matrice diagonale pour un tel corps ne me semble pas possible...

je ne vous demande donc pas de l'aide pour utiliser mes librairies, mais juste votre avis sur pareille matrice pour ce type de corps
Merci Beaucoup de votre aide
-----

[invite38685413]

la réunion des deux parallepipedes ne comportant qu'un seul plan de symétrie, il en effet etrange que tu ne trouve qu'une matrice diagonale. A moins que les valeurs des coté ne soit particulliere tu devrait trouver une matrice avec une diagonale et deux autres meme valeurs situé de chaque coté de la diagonale :
De ce genre

A F 0
F B 0
0 0 C

Il faudrait que tu nous en dise plus sur tes parallelogrames(dimension, position et masse)

[invite7e448ed9]

alors:
taille du corps jaune (en m):
x =0.134
y = 0.15
z = 0.102
poids = 2 kg

taille du corps vert (en carottes, ah non pardon en metres )
x = 0.134
y = 0.195
z = 0.063
poids = 3.6 kg
position par rapport au corps jaune :
x = 0
y = 0.023
z = -0.0835
ceci est donc un décalage de CM à CM

[bendesarts]

et le th de Huygens je pense qui pourrait servir : on calculer simplement l'inertie des 2 parallélépipède puis on ramène les matrices d'inertie au même point !!!!

Une matrice d'inertie : c'est en un point , dans une base et d'un solide !!!

th de huygens:

inertie en un point = inertie en G + matrice complémentaire de huygens

La matrice complémentaire de Huygens : c'est la matrice d'inertie de la masse du solide concentrée en G exprimée en C

Au passage, on peut remarquer que la matrice d'inertie est tjs minimal en G

inertie en un point A = inertie en G + matrice complémentaire de huygens

inertie en un point B = inertie en G + matrice complémentaire de huygens

Tu soustrais et tu obtient une relation qui permet de passer une matrice d'inertie d'un point quelconque à un autre point quelconque

Ici, tu en auras pas besoin : tu exprimes les inerties de chacun de tes parallélpipède en leur centre de gravité respectifs et il n'y qu'une matrice d'inertie à ramenée au centre de gravité de l'autre matrice et tu sommes et voilà

J'espère que j'aurais été suffisamment clair et çà pourra t'aider

Bonne chance

[A voir en vidéo sur Futura]

[bendesarts]

Je vous prie de bien vouloir me pardonner pour mon français : j'ai oublié un mot à chaque phrase

[invite38685413]

Quels sont les valeurs de la matrice que tu obtient ?

[olle]

il faut calculer les inerties des 2 masses séparément et en leur centre d'inertie respectif, puis ramener -> les 2 <- au centre d'inertie de l'ensemble complet.

g pas mon vieux cours sous la main et je ne me souviens plus du nom de la méthode simplicime pour translater le point en lequel on calcule l'inertie.

[invite7e448ed9]

alors j'obtiens comme matrices:
pour le corps jaune, p.rap à son CM
matrice I =
0.005484 0.000000 0.000000
0.000000 0.004727 0.000000
0.000000 0.000000 0.006743

pour le corps vert, p.rap a son CM
matrice I =
0.012598 0.000000 0.000000
0.000000 0.006578 0.000000
0.000000 0.000000 0.016794

[invite38685413]

il est normal d'avoir ce type de matrice pour chaque solide. Par contre la matrice totale n'est pas la somme de ces matrices. Il faut que tu appliques le theoreme d'huygens pour ramener une des matrice au point ou est definis l'autre matrice. C'est seulement si tes matrices sont definis au meme point que tu peux les ajouter.

[invite7e448ed9]

la matrice à laquelle je parviens pour ce corps formé de 2 rectangle, au positions décrites plus haut, est:
matrice I du body =
0.026335 0.000000 0.000000
0.000000 0.024165 0.000364
0.000000 0.000364 0.018930
CM :
0.000000
0.002246
0.010311
est ce que cela semble correct à qqn?
on m'a dit avant que cela devait ressembler à
A F 0
F B 0
0 0 C
alors que j'ai
A 0 0
0 B F
0 F C

qu'est ce que vous en pensez?
encore merci