Bonsoir,
Je galère avec un exercice en mécanique, je ne serais pas contre votre aide précieuse.
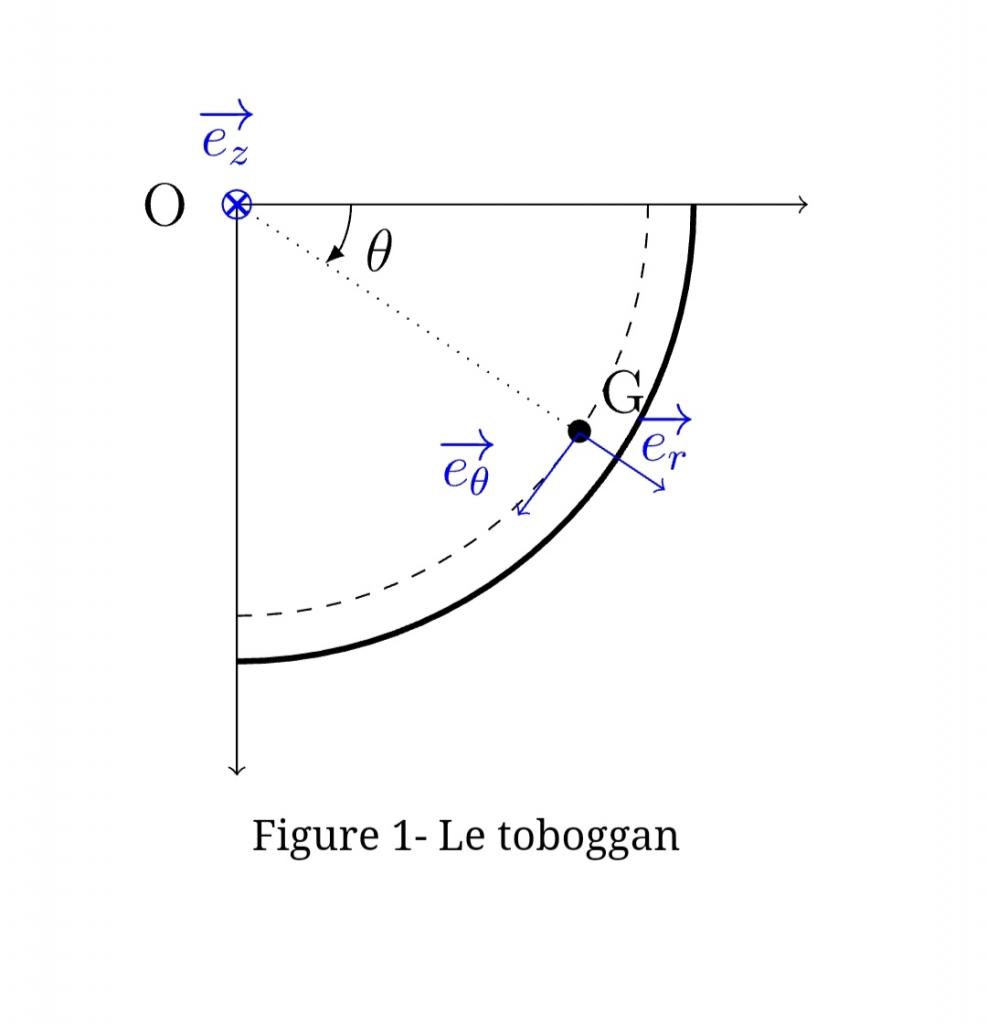
Un enfant glisse assis le long d’un toboggan. Celui-ci est une portion de cercle de centre O et de rayon 2.7m.Le centre de gravité de l’enfant, noté G, glisse tout au long de la descente à 20cm au dessus du toboggan.
L’angle que fait le rayon OG de la trajectoire de l’enfant avec l’horizontale est noté θ. Il est représenté sur la figure ci-contre.
Initialement, l’enfant s’élance d’une position θ0=15∘, sans vitesse initiale.En sortie du toboggan, l’angle θ vaut 90∘.
On considère que tout frottement est négligeable.
1) Appliquez le théorème du moment cinétique au point G afin de déterminer l’équation de son mouvement.
2) En déduire l’expression de la vitesse de l’enfant en fonction de l’angle θ.
Indice
En multipliant les termes de l’équation différentielle par une même grandeur, il sera possible de l’intégrer.
L'équation différentielle que j'obtiens pour la première question est θ'' = (g/r)cosθ, sachant que θ dépend de t. J'intègre donc l'expression pour avoir θ' et ensuite calculer Vg (r×θ). θ' c'est l'intégrale de (g/r)cosθ, ce qui donne : θ' = gcosθ/(rθ')+C, puisque θ' dépend de t. Alors θ'^2 = gcosθ/r + C, ça c'est mon raisonnement apparemment incorrect, j'aimerais savoir pourquoi. De plus, l'indice ne m'aide pas. Merci d'avance
-----
vous n'avez pas effectué l'intégrale !
désolée du dérangement et bonne soirée !