Le théorème de Gauss impose-t-il un univers neutre ?

[Marc]

Bonjour,

Je me pose la question d’électrostatique suivante dans un cadre de physique classique, avec un univers euclidien, plat (je ne fais pas de cosmologie) :
Le théorème de Gauss impose-t-il un univers neutre ?

Je pense que la réponse est « oui », et j’en donne une démonstration ci-après. Mais je ne trouve pas cette information (basique) dans la bibliographie, et donc, je doute, et :
- Etes-vous d’accord avec moi ?
- Avez-vous des références bibliographiques pour confirmer ou infirmer cette position ?
Merci de votre aide,
Marc
----


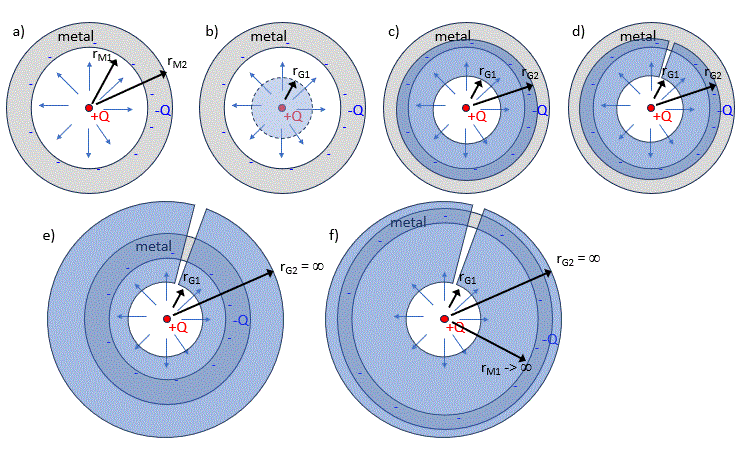
Sur la figure ci-dessus:
- a) Je considère une sphère métallique creuse, de rayon interne rM1 et de rayon externe rM2, en gris sur la figure,
Au centre, une charge +Q,
Sur la face interne de la sphère métallique, une charge répartie, d’intégrale -Q.
La face externe de la sphère métallique est neutre,
Au-delà, l’espace est neutre, jusqu’à l’infini.

- b) Pour appliquer Gauss, je choisis une sphère, centrée sur +Q, de rayon rG1 < rM1.
Je calcule facilement le champ sur cette sphère : E = Q/Eps0 x 1/ (4 Pi rG1²)
C’est un champ sortant de la sphère.

-c) Pour appliquer Gauss, je choisis un autre volume d’intégration : le volume compris entre les sphères de rayon rG1 et rG2, rG2 aboutissant à l’intérieur de la sphère métallique creuse : rM1 < rG2 < rM2.
Il s’agit d’un volume séparé du reste de l’espace par 2 surfaces disjointes. Je ne crois pas que ça pose de problème pour Gauss, mais,…

-d) Pour éviter toute discussion sur le volume du cas (c), je fais une petite entaille à travers ce volume. J’obtiens alors un volume tout à fait classique, avec un seul intérieur, un seul extérieur, et une seule surface frontière.
J’applique Gauss avec :
- une charge interne -Q
- pas de champ à rG2 puisqu’on est dans le métal
- et donc un champ à rG1 qui vaut E = -Q/Eps0 x 1/ (4 Pi rG1²)
C’est un champ sortant négatif, et c’est donc le même champ que celui calculé en (b). Heureusement !
Et je vérifie ici qu’il faut que la face interne de la sphère métallique creuse porte une charge exactement opposée à la charge centrale (de même que les charges sur les deux armatures d’un condensateur sont forcément opposées).

-e) J’étire rG2 au-delà de la sphère métallique creuse : rG2 > rM2.
Il ne se passe rien puisque la surface externe de la sphère métallique et l’espace extérieur sont neutres.
Et je peux étirer rG2 jusqu’à l’infini.

- f) Et je dilate finalement la sphère métallique creuse pour que ses rayons rM1 er rM2 tendent vers l’infini.
La densité surfacique de charge sur la face interne de la sphère tend vers zéro, mais son intégrale reste égale à -Q (sinon, le calcul de Gauss ne donne pas la bonne valeur du champ en rG1).
Je peux éventuellement supprimer la sphère métallique, mais je ne peux pas supprimer les charges qu’elle porte.

Et donc :
- toute charge +Q requiert une charge -Q
Ou, dit autrement, au choix :
- si un dessin ne montre qu’une charge +Q, alors une charge -Q est sous-entendue à l’infini,
- l’univers selon Gauss est neutre,
- l’espace étant un milieu linéaire, si on généralise à une distribution de charges, si la somme des charges à l’intérieur d’une surface close S est Qi, alors la charge à l’extérieur est -Qi.

Voilà ! D’accord ? Pas d’accord ?... Des références ?...
-----

[gts2]

Bonjour,

Dans votre présentation, il y a deux points
- vous supposez " l’espace est neutre, jusqu’à l’infini." et vous en déduisez l'espace est neutre
- vous supposez qu'il y a une coquille conductrice à l'infini et ensuite vous "supprimer la sphère métallique"

Pour ce qui est de la neutralité, c'est simple expérimentalement : la force électrique est nettement plus forte que la force gravitationnelle, or on ne "voit" à grande échelle que la force gravitationnelle, donc c'est la neutralité qui le permet.

[Paraboloide_Hyperbolique]

Bonjour,

Dans votre présentation, il y a deux points
- vous supposez " l’espace est neutre, jusqu’à l’infini." et vous en déduisez l'espace est neutre
- vous supposez qu'il y a une coquille conductrice à l'infini et ensuite vous "supprimer la sphère métallique"

En effet, le raisonnement donné est circulaire. De plus, "supprimer la sphère métallique" tout en gardant les charges est non-physique: ces charges sont des électrons (ou des trous d'électrons, selon le point de vue). Supprimer la dite sphère tout en gardant les charges revient à retirer des "trous" (ou des électrons) du système, donc à violer le principe de conservation de la charge.

Pour ce qui est de la neutralité, c'est simple expérimentalement : la force électrique est nettement plus forte que la force gravitationnelle, or on ne "voit" à grande échelle que la force gravitationnelle, donc c'est la neutralité qui le permet.

Tout à fait, sinon on verrait de spectaculaires décharges électriques à côté desquelles nos plus violent orages feraient figures d'étincelles.

Le théorème de Gauss, affirme en substances que si une quantité est conservée, toute variation de celle-ci au sein d'un volume fermé est forcément compensée par un flux de cette quantité au travers des frontières de ce volume.

[Marc]

Merci à vous deux pour vos réponses. Mais je vais argumenter davantage.

1-
Vous dites que mon raisonnement est circulaire.
En effet, je pars de l’hypothèse d’un univers neutre ; j’essaie de la casser ; et je montre que ce n’est pas possible.
Je ne crois pas que cette circularité suffise à disqualifier le raisonnement. Mais admettons…

Pour ce qui est de retirer le métal, je ne vois pas en quoi cela viole le principe de conservation de la charge. Il s’agit d’un métal non-neutre, qui porte -Q, disons des électrons en surplus. Enlever les ions et les autres électrons (en même nombre que les ions), en laissant -Q conserve la charge.

2-
Mais prenons le problème par l'autre bout, pour éviter la circularité.
Considérons la possibilité d’un univers non neutre. Du fait de la linéarité de l’univers et donc de la possibilité de superposer les états, cela revient à considérer la possibilité d’un univers avec une seule charge Q (je ferai un commentaire sur cette affirmation un peu plus loin, au point 4).
Considérons donc cette charge Q unique dans l’univers.
Gauss dit qu’on peut choisir le volume mathématique que l’on veut, de surface fermée S, pour appliquer sa formule sous forme intégrale ∬_S▒〖E.u dS〗=Q_i/ε_0 .
Si je considère une sphère de rayon rG1 centrée sur Q :
- si je choisis le volume à l’intérieur de la sphère, contenant Q, je trouve E=1/(4π r_G1 ²) Q/ε_0 ,
- si je choisis le volume complémentaire, s’étendant de rG1 à l’infini, sans charge, je trouve E=0.
Il y a donc incohérence. Et je dois mettre -Q à l’infini.

3-
Autre approche.
Un tube de force va d’une surface S1 avec une charge +Q à une surface S2 avec une charge opposée -Q.
Le champ étant radial, les tubes de force sont donc des angles solides de sommet Q :
- si je considère l’angle solide correspondant à la fraction αQ de Q, il doit aboutir à -αQ à l’infini,
- si je considère l’espace complet, 4π stéradians, correspondant à Q, il doit aboutir à -Q.

4-
L’univers est neutre car sinon les galaxies ne bougeraient pas comme elles le font.
Je connais l’argument mais :
- D’une part la réponse n’est pas aussi franche mais est : l’univers est neutre, ou presque neutre,
- D’autre part et surtout, ce n’est pas la question que je me pose.

Que l’univers soit vraiment neutre ou pas est une question de physique réelle.
Que l’équation du théorème de Gauss puisse décrire un univers non neutre est une question de mathématiques, décorrélée de la réalité.

Ma question est « dans le cadre du théorème de Gauss » peut-on envisager un univers non neutre ? Si la réponse est que Gauss est incompatible avec un univers non neutre, et si un jour on montre que l’univers n’est pas totalement neutre, alors il faudra modifier le théorème de Gauss.
D’ailleurs, c’est déjà prévu. J’ai fini par trouver un article qui explique qu’on peut imaginer un univers avec un surplus de charges d’un signe donné uniformément réparties, qui ne génèrent ni champ électrique, ni champ magnétique. Mais dans ce cas, le théorème de Gauss doit être modifié et est remplacé par les équations de Proca.
Voici l’article dont je parviens à lire les 3 premières colonnes. Après, je suis largué (et ça ne m’intéresse pas). (Notez que dans cet article le théorème de Gauss est écrit en unités cgs, comme div E=4πρ, et qu'à cause des charges réparties, il doit donc être modifié en div E=4πρ-µ²ϕ).

Cosmology of a Charged Universe, Aaron Barnes
https://articles.adsabs.harvard.edu/...00001.000.html

Mais c’est une réponse bien compliquée à la question que je pose. J’aurais espéré une explication électrostatique plus simple (avec une référence en anglais, si possible).

Qu’en pensez-vous ?

[A voir en vidéo sur Futura]

[stefjm]

Bonjour,
On peut appliquer le théorème de Gauss à la masse et il n'y a pas neutralité des masses.
Cordialement

[coussin]

Je ne sais pas trop pourquoi ce sujet se focalise sur le théorème de Gauss... Comme dit plus haut, celui-ci n'est qu'une "bête" conséquence de la conservation d'une quantité dans un volume donné...
La possibilité d'un Univers chargé électriquement est discuté dans cet article par exemple : https://arxiv.org/abs/1201.6585
Il semble impossible de falsifier cette hypothèse...

[gts2]

Pour ce qui est de retirer le métal, je ne vois pas en quoi cela viole le principe de conservation de la charge. Il s’agit d’un métal non-neutre, qui porte -Q, disons des électrons en surplus. Enlever les ions et les autres électrons (en même nombre que les ions), en laissant -Q conserve la charge.

Cela ne viole pas le principe de conservation de la charge , mais cela viole le principe de votre démonstration qui s'appuie sur la présence d'un métal.

Considérons donc cette charge Q unique dans l’univers.
Gauss dit qu’on peut choisir le volume mathématique que l’on veut, de surface fermée S, pour appliquer sa formule sous forme intégrale ∬_S▒〖E.u dS〗=Q_i/ε_0 .

Gauss dit bien qu'on peut prendre une surface quelconque mais la charge est à l'intérieur.

[Marc]

Bonjour à tous,
Le commentaire de stefjm me semble particulièrement pertinent : « Gauss s’applique aussi en gravitation, où il n’est pas question de masses de signe opposé ». Merci.
Je le développe ci-après ; vous me direz SVP ce que vous en pensez.
----
1-
En gravitation, une masse M émet des lignes de champ qui (dans un univers euclidien) partent vers l’infini en se diluant. Ces lignes partent vers « rien ». Elles n’ont pas de cible.
Pour appliquer Gauss, on peut :
- choisir un volume qui contient M, et on trouve un flux sortant positif,
- ou bien on peut choisir un volume qui ne contient pas M, et qui n’est que traversé par le flux, avec donc un flux sortant globalement nul,
- mais on ne peut pas choisir un volume incluant l’infini. En particulier, on ne peut pas choisir un volume ne contenant pas M, mais incluant l’infini. En effet ce volume reçoit du flux alors qu’il ne contient pas de masse (on pourrait imaginer d’y mettre une masse -M, absorbeuse de flux, mais ce serait un drôle d’objet, n’existant qu’à l’infini ; ça n’a guère d’intérêt).
Et donc, Gauss ne s’applique que sur des volumes finis. Ca ne restreint pas l’application pratique du théorème puisqu’on ne va jamais à l’infini.

2-
En électrostatique, on peut, au choix :
- Faire comme en gravitation, et laisser les lignes de champ émises par Q partir vers « rien » à l’infini,
- Ou bien leur donner des cibles, d’intégrale -Q.
Ca ne change rien pour le calcul du champ pour toute distance non-infinie, donc pour toute distance d’intérêt pratique.
Il y aura néanmoins des différences qu’on va discuter plus loin.

3-
Et il faudrait renommer ma conversation car le problème n’est pas de savoir si l’univers est neutre ou pas. Le sujet est :
« Quelle condition à l’infini vaut-il mieux choisir pour appliquer le théorème de Gauss ? » (pour en tirer des conséquences à des distances finies).

4-
Et donc, pour la gravitation, nous avons déjà dit qu’il valait mieux laisser les lignes de champ partir vers « rien » car des masses négatives -M ne correspondraient pas à grand-chose.

En électrostatique, par contre, nous avons vraiment le choix :
- si on laisse les lignes de champ partir vers « rien », l’intérêt est de faire le même choix qu’en gravitation. Il y a une cohérence.

- si pour toute charge Q, on place une charge distribuée -Q à l’infini, les avantages sont :

- On peut choisir un volume d’intégration incluant l’infini. C’est un avantage purement mathématique, mais c’est toujours bon à prendre,
- Mais surtout, ça introduit une continuité avec le cas le plus fréquent dans lequel on considère un système globalement neutre à l’échelle du laboratoire (un dipôle, un cristal, un circuit électronique,…) dans un univers globalement neutre. Dans ce cas, on peut bien sûr continuer à considérer les charges individuellement, chacune d’elle envoyant des lignes de champ à l’infini, mais dans la pratique, on regarde plutôt leur somme. Et si le système est neutre, aucune ligne de champ ne part à l’infini, et toutes les lignes de champ (ou plus précisément tous les tubes de champ) sont émises par des charges positives et sont nécessairement absorbées par des charges opposées. Chaque charge positive a sa cible négative.
En mettant une charge -Q à l’infini pour toute charge Q, on conserve donc cette propriété de couple +Q/-Q dans le cas moins fréquent où on envisage une distribution localement non neutre (encore une fois, ça ne change rien au calcul),
- Enfin (mais je sors de mon sujet d’univers euclidien), si on considère un espace fermé, l’horizon se referme, et une charge +Q au pôle nord impose une charge -Q au pôle sud. Voir l’équation 24 et la figure 2 de l’article de Pouria Pedram, https://arxiv.org/abs/0912.0225v1. Il y a donc aussi continuité avec ce raisonnement.

5- En conclusion, en électrostatique, on fait comme on veut, en mettant ou en ne mettant pas, pour chaque charge Q, une charge distribuée -Q à l’infini. Moi, je préfère la mettre.

[albanxiii]

Du fait de la linéarité de l’univers

Expression non définie, à partir de là, on peut dire n'importe quoi, vous vous arrangerez toujours pour avoir raison. Le reste est à l'avenant.
Désolé pour les participants à ce fil qui perdent leur temps.

[gts2]

Le sujet est : « Quelle condition à l’infini vaut-il mieux choisir pour appliquer le théorème de Gauss ? » (pour en tirer des conséquences à des distances finies).

Il faudrait alors préciser le sujet, le théorème de Gauss ne demandant aucune condition à l'infini.

[stefjm]

Expression non définie, à partir de là, on peut dire n'importe quoi, vous vous arrangerez toujours pour avoir raison. Le reste est à l'avenant.
Désolé pour les participants à ce fil qui perdent leur temps.

J'ai compris qu'on pouvait simplifier la problématique en ne considérant que deux charges résultantes +Q et -Q.

Il faudrait alors préciser le sujet, le théorème de Gauss ne demandant aucune condition à l'infini.

Mais il nécessite de pourvoir définir l'intérieur ce qui n'est pas si simple parfois, surtout quand on flirte avec l'infini.

[gts2]

Mais il nécessite de pourvoir définir l'intérieur ce qui n'est pas si simple parfois, surtout quand on flirte avec l'infini.

Il s'agit de définir l'intérieur d'une sphère !

Tant qu'à Gauss avec une surface infinie et donc avec des 0 * infini ou 0/0 ou infini/infini, je préfère laisser la parole aux matheux.

[coussin]

Le théorème de Gauss s'applique sur une surface/volume finis si je ne m'abuse.
Vouloir l'appliquer à des surfaces infinies, c'est sortir du domaine de validité de ce théorème : tout peut arriver...

[Deedee81]

Salut,

Le théorème de Gauss s'applique sur une surface/volume finis si je ne m'abuse.
Vouloir l'appliquer à des surfaces infinies, c'est sortir du domaine de validité de ce théorème : tout peut arriver...

Je suis d'accord. Il n'y a pas de surface à l'infini (sauf à considérer un univers fini mais alors bonjour les complications liées à la RG ou la topologie, je vois mal le théorème garder la même forme).
Et donc on peut avoir n'importe quel résultat. Le "flux sortant" peut être quelconque. Ca perd tout son sens.

Il est d'ailleurs fréquent de faire l'hypoth!se lors d'intégration par partie de : "pas de de fuite à l'infini" ou "les champs s'annullent à l'infini". Bref l'inifni est un fouteur de m....

De toute façon tout était dit dès le message 2 et les gesticulations suivantes ne changent rien (et le 9 est édifiant).
Notons que l'on peut déduire certaines propriétés sur l'univers à partir des lois de fondamentales (par exemple, à cause des neutrinos, la topologie d'une tranche spatiale ne peut pas être celle de Möbius ). Mais c'est (malheureusement) peau de chagrin.

J'ai compris qu'on pouvait simplifier la problématique en ne considérant que deux charges résultantes +Q et -Q.

Ben c'est ça le problème Si Q + -Q = 0 c'est facile de démontrer que le résultat est zéro
(mais le message auquel tu répondait reste correct, Albanxii a raison, l'univers linéaire c'est comique quantique même )

[Deedee81]

De toute façon tout était dit dès le message 2 et les gesticulations suivantes ne changent rien (et le 9 est édifiant).

Et je propose d'arrêter là. Je ne vois pas ce qu'on pourrait dire de plus (=> MP si vous voyez quelque chose de vraiment important)
et comme on était disons un tantinet border line avec le point 6 de la charte. On arrête.

Merci,

[Deedee81]

Salut,

Un message de Marc qui fait office de cloture de bon aloi.

Deux remarques, d'une part tu m'as dit (dans le MP) que tu n'avais pas été agressif et en effet, je le confirme. Le coté border line, la difficulté à expliquer et le chatouillage du point 6 de la charte, c'est ça qui a provoqué des réactions on va dire "désagréables". Beaucoup ici sont encore plus chatouilleux que la modération sur le respect des règles.

Ensuite, dans le message ci-dessous, en gras : ce passage est faux, le théorème devient inapplicable et même faux mathématiquement quand on l'étend à l'infini. Mais ce n'est pas grave dans la mesure où tu envisages le fait de mettre ou pas des charges à l'infini ce qui conduit à n'importe quelles solutions. Et en effet un titre comme « Que faut-il représenter à l’infini dans un problème d’électrostatique ? » aurait sans doute été mieux, j'y faisais allusion dans le message 14. Et de fait là je crois qu'on a fait le tour (de l'infini ).

Merci,

Bonjour,
Puisque c’est moi qui ai initié cette discussion, je me permets de faire une dernière intervention.

- J’ai écrit que l’univers était linéaire. Je me suis peut-être mal exprimé.
Si on considère N charges, et si chacune d’elles, si elle était seule, générerait un champ Ei (je parle du vecteur) en un point P de l’espace, alors les N charges ensemble génèrent en P un champ égal à la somme des Ei. Dit autrement, on peut travailler en superposant les états créés par chaque charge : le système est linéaire.

- Le théorème de Gauss s’occupe d’un volume fini et, en fonction de ce qu’il y a à l’intérieur, il définit ce qu’il en sort. Mais il ne dit rien de ce qui se passe à l’extérieur.

- Si on veut définir ce qui se passe à l’extérieur du volume, on a le choix :
* soit on ne met aucune charge à l’infini, et on peut traiter un problème dans lequel la somme des charges est non nulle (en particulier le cas d’une seule charge),
* soit on compense chaque charge Q par une charge -Q répartie à l’infini.
Ca ne change rien pour le calcul à des distances non-infinies.
Dans le deuxième cas, cela permet de considérer qu’on a systématiquement des doublets +Q/-Q et ça permet d’étendre Gauss pour l’appliquer sur un volume qui inclut l’infini.

- la discussion aurait plutôt pu s’appeler : « Que faut-il représenter à l’infini dans un problème d’électrostatique ? »

Personnellement, j’ai avancé dans ma réflexion : l’utilisation dans le cadre de la gravitation m’a permis de voir qu’on pouvait ne pas compenser à l’infini, à condition de s’interdire d’utiliser un volume d’intégration infini.
Je vous remercie.