Exercice de mécanique - Rouleau à bras

[Nekama]

Bonjour,

J'ai un problème de mécanique à proposer.

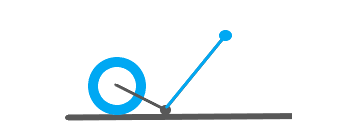
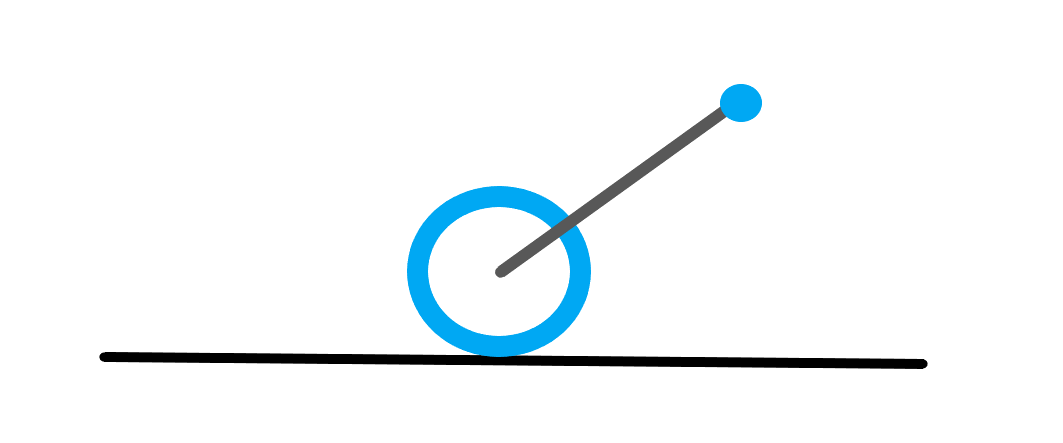
On considère un rouleau cylindrique creux de rayon R et de masse M (I = MR²).
Un bras de longueur d et de masse négligeable est fixé au centre O du rouleau. Il peut tourner librement autour de O.
A l'extrémité du bras, on a une poignée considérée ponctuelle et de masse m.
Le bras est initialement soulevé à un angle th_o proche de pi/6 avec l'horizontale puis lâché dans vitesse.

On considère que le coefficient d'adhésion (ou de frottement statique) µ_s est suffisamment élevé pour que le rouleau roule sans glisser.
On néglige les pertes par roulement.

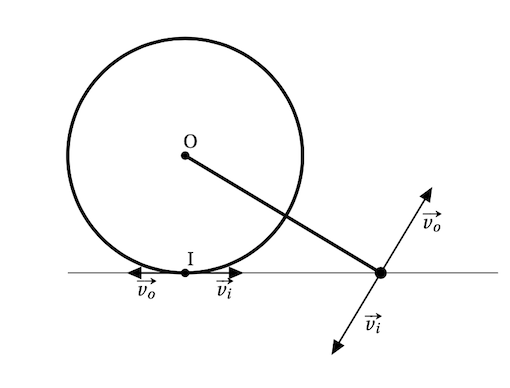
- Quelle est la vitesse (horizontale) du rouleau quand la poignée touche le sol (juste avant) ?
- Quelle est la position du rouleau et de la poignée au même moment (par rapport à leur position initiale) ?
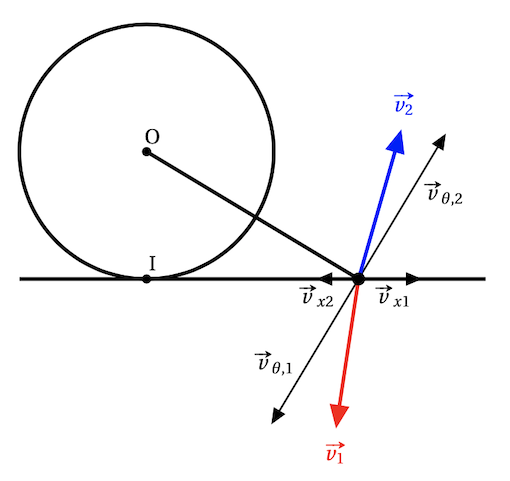
- Si on considère que le choc entre la poignée et le sol est purement élastique (la poignée est dans un caoutchouc souple et le sol en béton), que se passera-t-il ensuite ?
-----

[gts2]

Bonjour,

Un dessin ?
Parce que j'ai du mal à comprendre : au premier abord, on a l'impression d'un pendule dans un tube, ce n'est manifestement pas le cas puisque dans ce cas la poignée ne toucherait pas le sol, et même s'il le touchait il toucherait l'intérieur du tube pas le sol.

[Nekama]

Voici. J'aurais dû préciser : d > R.
Par contre m et M sont quelconques.

[gts2]

OK, compris.

1- Le théorème de l'énergie cinétique permet de trouver la vitesse
2- Le rouleau a tourné de α=π/6+π/2 donc s'est déplacé de Rα. Connaissant la position du rouleau, la position de la poignée s'en déduit
3- J'ai l'impression qu'on revient au point de départ.

[A voir en vidéo sur Futura]

[Nekama]

Merci pour ce premier retour.

On a 3 degrés de liberté : x, th (bras) et phi (rouleau).
Le roulement sans glissement lie x' et phi' et il en reste 2.

Le théorème de l'énergie cinétique donne une relation entre x'^2 et th'^2.
On n'a pas encore la vitesse et en plus on l'a au carré. On n'a pas son sens.

Je ne vois pas d'où vient la 2nd relation (?).

[gts2]

Mon OK n'était par correct ! J'avais supposé un lien entre le rouleau et le bras d'où un degré de liberté d'où méthode énergétique ...
En pensant à un rouleau à bras réel, c'est en effet incohérent.

Donc, en effet, cela se complique : peut-être théorème du moment cinétique sur la poignée, PFD sur la poignée pour trouver l'action du bras sur le rouleau, théorème du moment cinétique sur le rouleau.

[Nekama]

Que penses-tu de ceci et en particulier du point 2. ?

1. x pris vers la droite + Newton sur poignée dans référentiel centré en O en polaires et projeté sur e_th:

mdth'' = - mx'' - mg cos(th)

On suppose x'' << g et on multiplie par th' ; on utilise th'(0) = 0 et th(0) = th₀

th'² = 2g/d (sin(th_o) - sin(th)) [1a]

th' = - sqrt ( 2g/d (sin(th_o) - sin(th))) car th' < 0 [1b]

2. Energie sur le système complet

( 1/2 MR²phi'² + 1/2 Mx'² ) + 1/2 m ( x'² + d²th'² + 2 d |th'| |x'| cos(pi/2 + th)) = mgd (sin(th₀ - sin(th))

[Il doit bien y avoir une erreur quelque part, notamment de signe, non ]

Mais sinon, cela se réduit bien. En utilisant R phi' = x' et [1] qui permet de simplifier les parties en italique...

(2M+m) x'² - 2 m d |th'| |x'| sin(th) = 0

(2M+m) x'² + 2 m d th' |x'| sin(th) = 0 car th' < 0

|x'| = - 2m/(2M+m) d sin(th) th'

Comme en t ~ 0, x' < 0, on a :

x' = 2m/(2M+m) d sin(th) th' [2]

2a. En introduisant [1b] dans [2], on obtient

x' = - 2m/(2M+m) sin(th) sqrt (2gd (sin(th_o) - sin(th))) [3a]

2b. En intégrant [2], on obtient :

x = 2m/(2M + m) d ( cos(th₀ - cos(th) ) [3b]

Cela te parait-il correct ?

[gts2]

mdth'' = - mx'' - mg cos(th)

Il manque la projection du - mx'' par , mais comme on le néglige par la suite.
Mais dans ce cas, utiliser tout de suite le théorème de l'énergie cinétique permet d'arriver immédiatement à :

( 1/2 MR2phi'2 + 1/2 Mx'2 ) + 1/2 m ( x'2 + d2th'2 + 2 d |th'| |x'| cos(pi/2 + th)) = mgd (sin(th0 - sin(th))

Les valeurs absolues sont inutiles, c'est un calcul algébrique.
Il y a en effet une erreur de signe sur l'énergie potentielle Ep=mgh= et donc
Il y a bien simplification (sous l'hypothèse initiale)
Remarque avec un rouleau (donc plein), le premier terme est 1/4 (1/2 pour l'énergie cinétique et 1/2 pour le moment d'inertie)

x' = 2m/(2M+m) d sin(th) th' conduit ensuite directement par intégration à x = 2m/(2M + m) d ( cos(th0 - cos(th) ) [1b] non nécessaire.

Cela te parait-il correct ?

A l'approximation et le moment d'inertie près, oui.
Pour le moment d'inertie, il faut juste corriger, pour l'approximation, il faut la vérifier.

[Nekama]

Merci pour ton retour.

Remarque avec un rouleau (donc plein), le premier terme est 1/4 (1/2 pour l'énergie cinétique et 1/2 pour le moment d'inertie)

L'énonce indiquait : "On considère un rouleau cylindrique creux de rayon R et de masse M (I = MR2)."

x' = 2m/(2M+m) d sin(th) th' conduit ensuite directement par intégration à x = 2m/(2M + m) d ( cos(th0 - cos(th) ) [1b] non nécessaire.

L'énonce demandait aussi : "- Quelle est la position du rouleau et de la poignée au même moment (par rapport à leur position initiale) ?"

J'ai deux questions du coup :

1/
Si on applique la conservation de la quantité de mouvement, on trouve la moitié pour x' : x' = 1m/(2M+m) d sin(th) th' [2]
Est-ce à cause de la force d'adhérence (frottement) f ? Mais elle ne travaille pas et c'est la seule force externe horizontale... Comment l'expliquer ?
Si oui, est-ce qu'on pourrait trouver f ?

2/
Si on suppose qu'il y a un rebond parfaitement élastique, que se passe-t-il ensuite ?

[gts2]

OK pour le rouleau creux.

La conservation de la quantité de mouvement, c'est pour un système isolé, ce n'est pas le cas ici à cause en effet de la force de frottement.

J'ai essayé le calcul exact : c'est compliqué et je ne suis pas sûr de l'approximation.

[Nekama]

Effectivement, de manière générale, on ne peut pas considérer x'' cos(th) < g sin(th)

J'ai dérivé x' par rapport à t en remplaçant th' par son expression est malheureusement la condition n'est pas respectée...

Il faudrait m << M.

[gts2]

Si c'est un rouleau à bras de jardinier parait raisonnable.

Pour le choc, cela change les vitesses de signe, les équations ne changent pas, donc retour à l'état initial.

[Nekama]

Je ne suis pas convaincu que le bras remonte à sa position initiale.

Pour qu'il remonte à sa position initiale, il faudrait que l'énergie cinétique que le rebond procure à la poignée soit égale à l'énergie potentielle initiale de la poignée.

Ce n'est pas nécessairement le cas. Une partie de l'énergie cinétique a été transmise à la rotation du rouleau.

---

Il faudrait dès lors voir si lors de la remontée, l'énergie du rouleau se retransmet à la poignée pour la faire remonter.

C'est difficile à concevoir et pénible à calculer à cause de l'angle avec lequel la poignée percute le sol.

Je pense que ça se voit bien si on modifie un peu l'énoncé juste pour que les conditions initiales du rebond soient différentes.



---

Les équations du mouvement sont les mêmes.

Lors de la chute on n'a pas conservation de la quantité de mouvement vu la présence de la force externe f qui permet de transmettre une partie de l'énergie dans la rotation du rouleau.

On l'aurait si le rouleau était ponctuel, et on pourrait voir le problème comme un problème où le centre de masse reste immobile. Mais ici il ne l'est pas et il a bougé.

Lors de la remontée, comme la poignée en montant va aussi vers l'avant à cause de la rotation, une impulsion est fournie au rouleau vers l'arrière.

Mais tout comme lors de la chute on n'a pas conservation de la quantité de mouvement, on ne l'a pas non plus lors de la remontée.

Le rouleau va perdre une partie de son énergie cinétique de rotation mais pas tout.

Et par conservation de l'énergie, la poignée ne remonte pas dans sa position initiale...

Qu'en penses-tu ?

[gts2]

Pour qu'il remonte à sa position initiale, il faudrait que l'énergie cinétique que le rebond procure à la poignée soit égale à l'énergie potentielle initiale de la poignée.
Ce n'est pas nécessairement le cas. Une partie de l'énergie cinétique a été transmise à la rotation du rouleau.

Oui, mais le rouleau participe au choc.

Il faudrait dès lors voir si lors de la remontée, l'énergie du rouleau se retransmet à la poignée pour la faire remonter.

Bien sûr, ce sont les mêmes équations donc le transfert va se faire de la même manière (mais avec t -> -t)

C'est difficile à concevoir et pénible à calculer à cause de l'angle avec lequel la poignée percute le sol.
Je pense que ça se voit bien si on modifie un peu l'énoncé juste pour que les conditions initiales du rebond soient différentes.

Il n'y a rien à calculer : il suffit de changer les signes. (i pou in avant et o pour out après)

Mais tout comme lors de la chute on n'a pas conservation de la quantité de mouvement, on ne l'a pas non plus lors de la remontée.

Oui, mais en quoi est-ce un problème ?

Le rouleau va perdre une partie de son énergie cinétique de rotation mais pas tout.

Je ne vois pas pourquoi le rouleau garderait une partie de l'Ec.

Le problème est dans l'approximation : on calcule à ε près et en reportant cette valeur (à ε près) dans l'Ec on se retrouve avec des termes petits. Autrement dit on calcule des ε à ε près, ce n'est pas très précis...
je ne dis pas que le calcul est faux mais il faut au moins regarder de plus près.

[Nekama]

Je suis d'accord sur l'erreur de négliger la force fictive (mx'') dans le calcul de th''.
Je n'ai trouvé aucune approche sans modifier l'énoncé ou sans passer à une approche numérique.

Si on étudie le système complet, quelle est la bonne écriture :

x est pris vers la gauche.

(a) (M+m)x'' = f
(b) (M+m)x'' = f - mdth'²
(c) autre chose

[gts2]

a) f est la seule force extérieure horizontale.
Remarque : ici x est ici la position du centre d'inertie (rouleau, poignée) mais avec l'approximation , cela peut marcher.
Remarque bis : cela permet de calculer f connaissant x (je suppose que f est la compensante tangentielle de l'action du sol sur le rouleau), dans l'autre sens ...

Je n'ai pas non plus trouvé de méthode analytique, mais je ne suis peut-être pas très éveillé.

[Nekama]

Encore merci pour tes inputs.

Je voudrais résoudre sans prendre M >> m car cela fausse la physique du problème.

Effectivement, c'est le centre de masse.

Bonjour l'arrivée des x en plus des x' du coup...

[gts2]

Je voudrais résoudre sans prendre M >> m car cela fausse la physique du problème.

J'ai bien peur qu'il n'y ait pas de solution analytique.

[Nekama]

Pour revenir au message #14.

Quand une balle en caoutchouc percute le sol, après le rebond elle conserve sa vitesse horizontale mais sa vitesse verticale est inversée.

On a symétrie par rapport au sol mais pas par rapport à la verticale.

Ici, quand la poignée va percuter le sol, il doit se produire la même chose et l'impulsion initiale donnée à la poignée est celle en rouge.

On doit alors considérer le choc au travers du bras entre le rouleau et la poignée.

C'est seulement si le rouleau était de masse infinie (et immobile) qu'on aurait la réflexion de la composante verticale de la vitesse.

choc.png

[Nekama]

Toujours relativement à #14

La vitesse du point de contact entre le sol et le rouleau vaut 0 avant le choc.

Cette vitesse est l'addition de la vitesse du CM du rouleau et de la rotation de son extrémité (x' - R phi')

phi' après le choc ne change pas... Là aussi, il y a "brisure" de symétrie.

x' va très probablement brusquement changer.

Par la suite, le chariot va immanquablement glisser, le temps que la force de frottement dynamique rétablisse le RSG...

Il n'y a plus symétrie non plus dans les équations...

[gts2]

C'est seulement si le rouleau était de masse infinie (et immobile) qu'on aurait la réflexion de la composante verticale de la vitesse.

Je m'étais bien placé dans le cas pour le dessin.
Si m devient du même ordre que M, le choc sur le bras pourrait aller jusqu'à donner une vitesse verticale au rouleau ...

Un dessin un peu plus réaliste mais toujours sous la même approximation : j'ai pris des vitesses de rouleau après/avant pas tout fait opposées.
est la vitesse orthoradiale dans le référentiel lié au rouleau. v_x est la vitesse du rouleau. v la vitesse de la poignée dans le référentiel du sol. 1 avant le choc, 2 après.

[gts2]

phi' après le choc ne change pas.

Je ne vois pas pourquoi.

Par la suite, le chariot va immanquablement glisser.

Probablement si m est de l'ordre de M.

[Nekama]

Pour le bras, je me posais la question de savoir s'il remontait à sa position initiale. Il faudrait M infini, çad >> m. Ok.

Dans mes notations, j'ai pris th pour le bras. Quand j'ai écrit phi, je pensais au rouleau. Son phi'(t_choc) ne varie pas directement après le choc

---

Merci pour tes différentes remarques et inputs.