Looping d'une bille (non ponctuelle)

[Nekama]

Bonjour,

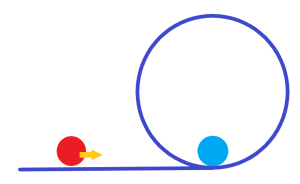
La bille ponctuelle que l'on envoie dans un cerceau et qui doit en réaliser un tour complet est un exercice assez traditionnel.
Je propose de passer de la bille ponctuelle à la bille de dimension non nulle.

On dispose ainsi de billes de couleurs de masse M, de rayon R et de moment d'inertie I = 2/5 MR².
On a également un rail de forme circulaire avec un rayon interne r = 5R.

L'objectif est de propulser une bille rouge à une vitesse v_o de telle sorte qu'après qu'elle ait percuté la bille bleue, cette dernière fasse un tour complet du rail circulaire en y restant accolé.

Le challenge et la question sont de déterminer l'ensemble des conditions nécessaires pour y parvenir...

nb: on néglige les frottements par roulement et on ne considère de frottement dynamique que s'il n'y pas roulement sans glissement.


-----

[Black Jack 2]

Bonjour,

La phrase "on ne considère de frottement dynamique que s'il n'y pas roulement sans glissement." n'est pas claire.

Au moment du choc, la bille bleue va démarrer en glissement sans roulement, elle se mettra à rouler progressivement grâce au frottement dynamique.

Autre remarque :
Que la bille soit ou non ponctuelle ne change pas grand chose.
L'énergie cinétique d'une bille de masse m et de rayon R qui roule sans glisser est 1/2.m.v² + 1/2.(2/5.m.R²).w² avec w = v/r
Donc Ecinétique = 0,7.m.v² (translation + rotation)
On remarque que c'est indépendant de R, et donc vrai aussi si R --> 0, donc pour une bille "ponctuelle" (de masse non nulle évidemment)

Si on a une bille qui roule, la nature du problème reste la même avec une bille "ponctuelle" ou non.

Ce qui arrive souvent est qu'on parle d'un objet ponctuel et on suppose généralement qu'il glisse sans rouler.
Mais en précisant qu'on a une bille ... on n'est pas dans le cas d'un mobile qui glisse sans rouler (sauf si le coefficient de glissement dynamique est nul).

La bille peut-elle être en glissement partiel en passant au point haut ou bien doit-elle être en roulement sans glissement ?

Bref, il faudrait un énoncé plus précis.

[Nekama]

Bonjour,

La phrase "on ne considère de frottement dynamique que s'il n'y pas roulement sans glissement." n'est pas claire.

Au moment du choc, la bille bleue va démarrer en glissement sans roulement, elle se mettra à rouler progressivement grâce au frottement dynamique.

A if not(B) signifie que not(B) -> A
Et donc, il y a bien un frottement dynamique (A) s'il n'y a pas de roulement sans glissement (B).
L'énonce dit la même chose que toi.

Autre remarque :
Que la bille soit ou non ponctuelle ne change pas grand chose.
L'énergie cinétique d'une bille de masse m et de rayon R qui roule sans glisser est 1/2.m.v² + 1/2.(2/5.m.R²).w² avec w = v/r
Donc Ecinétique = 0,7.m.v² (translation + rotation)
On remarque que c'est indépendant de R, et donc vrai aussi si R --> 0, donc pour une bille "ponctuelle" (de masse non nulle évidemment)

Si on a une bille qui roule, la nature du problème reste la même avec une bille "ponctuelle" ou non.

Il n'y a pas que la conservation de l'énergie comme principe.
Et si effectivement, à ce niveau, passer au ponctuel revient à modifier la masse pour avoir une masse apparente (nommons l'astuce de la sorte).

Mais ce raccourci n'est pas vraie pour tous les principes.
Si un jour tu t'intéresses au billard et que tu essaies d'étudier le choc des billes, tu peux voir pourquoi.

La bille peut-elle être en glissement partiel en passant au point haut ou bien doit-elle être en roulement sans glissement ?
(...)
Bref, il faudrait un énoncé plus précis.

Dans le monde scolaire, on aime bien avoir des applications où toutes les données sont fournies.
Dans la vie réelle, on n'a pas toutes les données et il faut faire des hypothèses.

L'énonce dit aussi : "Le challenge et la question sont de déterminer l'ensemble des conditions nécessaires pour y parvenir..."

Et donc, on peut :
1. soit de n'étudier qu'un cas, celui où il y a RSG
2. soit un autre cas, où il y a glissement.

[Black Jack 2]

A if not(B) signifie que not(B) -> A
Et donc, il y a bien un frottement dynamique (A) s'il n'y a pas de roulement sans glissement (B).
L'énonce dit la même chose que toi.

"Il n'y a pas que la conservation de l'énergie comme principe.
Et si effectivement, à ce niveau, passer au ponctuel revient à modifier la masse pour avoir une masse apparente (nommons l'astuce de la sorte).

Mais ce raccourci n'est pas vraie pour tous les principes.
Si un jour tu t'intéresses au billard et que tu essaies d'étudier le choc des billes, tu peux voir pourquoi."



Dans le monde scolaire, on aime bien avoir des applications où toutes les données sont fournies.
Dans la vie réelle, on n'a pas toutes les données et il faut faire des hypothèses.

L'énonce dit aussi : "Le challenge et la question sont de déterminer l'ensemble des conditions nécessaires pour y parvenir..."

Et donc, on peut :
1. soit de n'étudier qu'un cas, celui où il y a RSG
2. soit un autre cas, où il y a glissement.

"Mais ce raccourci n'est pas vraie pour tous les principes.
Si un jour tu t'intéresses au billard et que tu essaies d'étudier le choc des billes, tu peux voir pourquoi."

Bof.
- Le rayon n'intervient pas dans l'expression de l'énergie cinétique en roulement pur. (0,7.m.v²)
- Le rayon n'intervient pas dans la durée pour passer de glissement à roulement : t = 2vo/(7µg) (avec vo la vitesse au moment du choc de la bille de choc)
- Le rayon n'intervient pas dans la vitesse de roulement (hors perte de roulement) : v = 5/7 vo
- Le rayon n'intervient pas dans la distance parcourue entre le choc et l'instant où la boule choquée est en roulement pur : 12/49 vo²/(µ.g)
- Pour la direction des billes après le choc, on a besoin d'un rayon ... mais il peut être aussi petit qu'on veut.
Cela au billard (surface horizontale).

Si tu as une caractéristique où le rayon modifie le type de raisonnement pour répondre au problème posé, je serai heureux de l'apprendre.

Je passe la main aux volontaires qui vont avoir la patience de faire toutes les hypothèses possibles et imaginables pour traiter tous les cas.

[A voir en vidéo sur Futura]

[Nekama]

Si tu as une caractéristique où le rayon modifie le type de raisonnement pour répondre au problème posé, je serai heureux de l'apprendre.

JP,

Dans l'approximation ponctuelle, si une bille percute un bille avec un choc purement élastique, l'entièreté de la qtt de mouvement et de l'énergie sont transmises. La bille initialement en mouvement s'arrête. La suivante repart avec la même vitesse.

Dans la réalité, en supposant les parois lisses (et de toute manière vu la faible surface de contact), la quantité de mouvement transmise sera de m(2K/m*)^1/2 et pas de m*(2K/m*)^1/2 comme si elles avaient été ponctuelles. La bille qui repart va initialement repartir à la même vitesse et glisser, mais elle ralentit non pas uniquement à cause de µ_d, comme tu le penses, mais aussi à cause de l'énergie cinétique transmise à la rotation. En pratique, si tu tapes légèrement sur une balle de billard (sans effet) et qu'elle va percuter une autre, les 2 repartent. Fais l'expérience.

Je passe la main

toutes les hypothèses possibles et imaginables pour traiter tous les cas

C'est mieux ainsi...

Le cas le plus simple est d'imposer à la bille de rouler dans glisser sur tout le rail.
Sinon, il y a une transition d'un état de glissement à un état de roulement sans glissement et c'est très compliqué.
De plus, vu qu'on considère µ_d, quand elle glisse tout du long, elle va se mettre à tourner aussi, et ça complique les calculs également.

[Black Jack 2]

JP, connais pas ?

"Dans l'approximation ponctuelle, si une bille percute une bille avec un choc purement élastique, l'entièreté de la qtt de mouvement et de l'énergie sont transmises. La bille initialement en mouvement s'arrête. La suivante repart avec la même vitesse."

Ben non.
Avec une bille dont le rayon tend vers 0 (= 0 ne veut rien dire), les phénomènes sont les mêmes qu'avec une bille de rayon non nul.
Il suffit d'établir les relations physiques avec R non nul ... et puis de voir ce qu'elles deviennent avec R tendant vers 0.

Et là tu te plantes encore.
Lorsqu'une bille (de rayon R) roule sans glisser et percute une autre bille (de mêmes caractéristiques) (suivant la direction qui relie les 2 centres).
La bille percutée part (juste après le choc) en glissement pur (avant de passer en roulement pur après une phase de glissement+roulement) et la bille qui percute s'arrête de "translater" (au moment du choc) mais continue à tourner autour de son axe et ensuite, par le frottement sur le tapis (si billard), la rotation de la bille sur elle même se transforme progressivement en translation et la bille fini par continuer à avancer en rotation pure.

Tout cela est facile à mettre en équation ... et on peut alors faire tendre le rayon des billes vers 0, pour constater que les phénomènes n'en sont pas affectés. (J'ai donné quelques relations liées au billard dans mon post précédents qui montrent que R n'y intervient pas)

Si on parle de BILLE ponctuelle (c'est une vue de l'esprit indiquant que R tend vers 0, pas égal 0) , les phénomènes sont exactement les mêmes que pour une bille de rayon ne tendant pas vers 0.

Dans les problèmes bien écrits (c'est loin d'être toujours le cas), on emploie "mobile ponctuel" et on ajoute "qui glisse". Cela permet alors de traiter les problèmes sans les roulements et sans les pertes de frottement aérodynamique et quelques rares autres (Archimède par exemple).

Mais, si on stipule "BILLE" qu'elle soit ou non "ponctuelle" (R tendant vers 0) ne change rien pour la plupart des phénomènes. On peut juste négliger les effets de frottement aérodynamique et quelques autres, mais certainement pas les effets liés au roulement (énergie cinétique, vitesses après choc, vitesse de croisière stabilisée en roulement pur, distance de phase glissement + roulement, durée de cette phase, ...

Ceci dit, on ne peut pas, dans le problème posé (sans faire une énorme approximation) considérer que la bille bleue va faire l'entièreté du tour en roulant sans glisser puisqu'elle est déjà obligée de glisser après le choc avec la bille rouge. Elle va passer par une période de glissement + roulement dont les caractéristiques dépendent de la force de frottement dynamique de la bille avec le cerceau, avec la difficulté que cette force n'est pas constante (comme sur un billard horizontal) mais est proportionnelle à la réaction normale du cerceau sur la boule (donc qui varie avec la vitesse et la composante radiale du poids variant avec l'angle parcouru)...

Mais on peut, par exemple, imposer que la bille soit en rotation pure (sans glissement) au passage par le sommet et faire les calculs en conséquence ... il faut cependant tenir compte de la phase de "démarrage" qui est forcément en glissement + roulement et qui s'accompagne d'une perte d'énergie (en plus de la variation d'énergie potentielle) ...

Je n'essaye pas, puisqu'il semble bien que nous ne soyons déjà pas en phase avec des principes de base.
Mais je lirai avec intérêt (sans intervenir), les réponses ou avis qui seront fournis.

[Nekama]

JP,

Je n'ai plus de temps à perdre avec toi avec tes billes ponctuelles
Si tu ne comprends pas, tant pis.

Merci de ne plus intervenir sur ce fil.
D'autres le feront s'ils en ont envie. Ou pas.

[Black Jack 2]

"Si tu ne comprends pas, tant pis."

[coussin]

Bonjour,

La phrase "on ne considère de frottement dynamique que s'il n'y pas roulement sans glissement." n'est pas claire.

Au moment du choc, la bille bleue va démarrer en glissement sans roulement, elle se mettra à rouler progressivement grâce au frottement dynamique.

Autre remarque :
Que la bille soit ou non ponctuelle ne change pas grand chose.
L'énergie cinétique d'une bille de masse m et de rayon R qui roule sans glisser est 1/2.m.v² + 1/2.(2/5.m.R²).w² avec w = v/r
Donc Ecinétique = 0,7.m.v² (translation + rotation)
On remarque que c'est indépendant de R, et donc vrai aussi si R --> 0, donc pour une bille "ponctuelle" (de masse non nulle évidemment)

Si on a une bille qui roule, la nature du problème reste la même avec une bille "ponctuelle" ou non.

Ce qui arrive souvent est qu'on parle d'un objet ponctuel et on suppose généralement qu'il glisse sans rouler.
Mais en précisant qu'on a une bille ... on n'est pas dans le cas d'un mobile qui glisse sans rouler (sauf si le coefficient de glissement dynamique est nul).

La bille peut-elle être en glissement partiel en passant au point haut ou bien doit-elle être en roulement sans glissement ?

Bref, il faudrait un énoncé plus précis.

Bonjour Black Jack

J'ai trouvé un sujet StackExchange qui semble répondre au problème, regarde la première réponse ici : https://physics.stackexchange.com/qu...-loop-question.
J'y vois ce que tu as écrit (le 0.7 qui est 1/2 + 1/5 pour énergie cinétique + rotation). Ensuite, je vois que le rayon de la bille survit dans l'expression finale juste pour une histoire de mesurer correctement les altitudes de la bille (?). Je ne sais pas si ça s'applique ici où c'est une autre bille qui pousse, il ne s'agit pas de trouver une hauteur de lâcher...

J'espère que ça peut être utile...

[Black Jack 2]

Bonjour Black Jack

J'ai trouvé un sujet StackExchange qui semble répondre au problème, regarde la première réponse ici : https://physics.stackexchange.com/qu...-loop-question.
J'y vois ce que tu as écrit (le 0.7 qui est 1/2 + 1/5 pour énergie cinétique + rotation). Ensuite, je vois que le rayon de la bille survit dans l'expression finale juste pour une histoire de mesurer correctement les altitudes de la bille (?). Je ne sais pas si ça s'applique ici où c'est une autre bille qui pousse, il ne s'agit pas de trouver une hauteur de lâcher...

J'espère que ça peut être utile...

Bonjour,

Cela ressemble, sur la réponse 2, l'autre étant fausse.

La différence (mais plus qu'importante) est que dans cet exercice (ton lien), la bille est placée au départ pour pouvoir rouler sans glisser.

Dans l'exercice proposé dans ce sujet-ci, il y a au départ (après le choc) du glissement qui s'accompagne forcément de perte d'énergie pour transiter vers une phase de roulement seul ... avec la difficulté que la force de frottement dynamique lors de cette phase n'est pas constante (comme elle le serait en billard à plat, par exemple).

Une autre difficulté est que si on veut que la bille passe au sommet de la boucle en roulant sans glisser (après avoir glissé forcément dans le bas de la boucle), en plus de faire un calcul énergétique pour assurer que le looping puisse se faire, il faut s'assurer que la bille ne va pas se remettre à glisser en approchant du sommet.

[coussin]

Néanmoins, cette histoire que le rayon de la bille apparaisse à la fin me semble correct. En effet, dans le cas limite où R=r, la bille ne change jamais d'altitude en fait.

[Black Jack 2]

Néanmoins, cette histoire que le rayon de la bille apparaisse à la fin me semble correct. En effet, dans le cas limite où R=r, la bille ne change jamais d'altitude en fait.

Il y a confusion là.
Je n'ai jamais dit que R (rayon de la boucle) et r (rayon de la bille) pouvaient être confondus.
Il faut évidemment R > r.
Ce que je dis est que la résolution du problème est la même que r soit grand (bien que < R) ou bien que r soit quasi nul.

Par exemple l'énergie cinétique d'une bille qui roule sans glisser est Ec = 1/2.m.v² + 1/2.J.w² = 1/2.m.v² + 1/2*2/5.m.r²*v²/r² = 0,7.m.v² indépendant du rayon de la bille).
On voit que 2 billes (pleines homogènes) de même masse m, roulant sans glissement à la vitesse v ont la même énergie cinétique, soit 0,7.m.v² et ceci même si les 2billes sont de rayon différents (donc même si une des billes a un rayon quasi nul)

On peut faire les calculs pour calculer des distances de glissement ou des durées de glissement ou ... n'importe quoi de nécessaire à résoudre le problème posé, on trouvera des expressions indépendantes du rayon de la bille.

Si le rayon se retrouve dans une expression nécessaire à la résolution de ce problème, il y a toujours moyen de le virer.

Par exemple, l'énergie cinétique de rotation de la bille est Ecr = 1/2.I.v²/r² qui a l'air de dépendre de r, sauf que ...
On a I = 2/5.m.r² et donc Ecr = 1/2.(2/5.m.r²).v²/r = 0,2.m.v² (donc indépendant de r)

[coussin]

Bien sûr, je suis d'accord avec tout ce que tu écris
Mais la vitesse minimale pour le looping va dépendre, in fine, de l'altitude que la bille devra gravir lors du looping. Et cette altitude fera intervenir le rayon de la bille.

[Black Jack 2]

Bien sûr, je suis d'accord avec tout ce que tu écris
Mais la vitesse minimale pour le looping va dépendre, in fine, de l'altitude que la bille devra gravir lors du looping. Et cette altitude fera intervenir le rayon de la bille.

Penses-tu que la manière de résoudre le problème est différente en fonction de la valeur du rayon de la bille ?
Le problème peut être résolu en littéral avec r quelconque et faire tendre r vers 0 tout à la fin si tu veux. Cela ne doit pas amener une impossibilité quelconque. Tous les "phénomènes" physiques utiles pour la résolution du problème sont les mêmes quelle que soit la valeur du rayon de la bille (même si elle tend vers 0).

[Nekama]

Bien sûr, je suis d'accord avec tout ce que tu écris
Mais la vitesse minimale pour le looping va dépendre, in fine, de l'altitude que la bille devra gravir lors du looping. Et cette altitude fera intervenir le rayon de la bille.

Effectivement. C'est déjà une des premières raisons pour lesquelles on ne peut pas juste remplacer m par m* = m + 2/5 m pour résoudre le problième.
Mais cela intervient également à d'autres endroits.

1. Maintien sur le rail

Il faut donc que N > 0
L'endroit le pire pour respecter cette condition est tout-au-dessus puisque c'est là que F_c est la plus faible et -mgcos(th) la plus grande.

mv²/(r-R) = mg

v_f² > g(r-R)

2. vitesse nécessaire en dessous du rail pour atteindre le dessus du rail

On considère que la bille roule sans glisser sur le rail.
On écrit la conservation de l'énergie

K_i = K_f + U_f

1/2 m*v_i² = 1/2 m*v_f² + 2mg(R-r)

v_i² = v_f² + 20/7 g(r-R) > 27/7 g(r-R)

3. Choc entre 2 billes

On doit avoir au pied du cerceau un bille qui RSG avec v_i² > 27/7 g(r-R)

Le problème est que quand une bille entrechoque une autre à l'arrêt, la seconde démarre en glissant linéairement et va perdre de l'énergie avant de se mettre à RSG...

Si on étudie la bille percutée :

x'(o) = v_o

mx'' = - µmg et 2/5 m Rph'' = µmg

x' = -µgt + v_o et Rphi' = 5/2 µgt

v_c = x' - R phi' = v_o - 7/2 µgt

v_c = 0 et t_c = 2v_o/7µg

A ce moment :

x' = v_o - µg 2v_o/7µg = 5/7 v_o

x = ... = 12/49 vo²/µg = d

Pour que la bille percutée entame l'ascension en RSG, il faut donc qu'au moment du choc, elle se soit trouvée à au moins une distance d du pied des rails.

Il faut faut que :

x'² = 25/49 v_o² > 27/7 g(r-R)

v_o² > 27*7/25 g(r-R)

Pour le fun, on peut calculer : W = - 12/49 mv_o² est indépendant de µ_d

4. RSG tout le long du parcours.

Il faut que la force qui de frottement statique qui empêche le glissement : f > µN

f = m(r-R) th'' + mg sin(th) < µ (mv² / (r-R) + mg cos(th)) à tout moment.


nb: si on fait tendre R vers 0 à la fin ou si on ne distingue pas m* et m, on n'arrive évidemment pas au bon résultat.

[coussin]

Penses-tu que la manière de résoudre le problème est différente en fonction de la valeur du rayon de la bille ?

Si le problème est "quelle est la vitesse minimale pour que la bille fasse le looping ?" alors oui bien sûr car cette vitesse minimale dépendra de l'altitude à gravir lors du looping et que cette altitude est 2(R-r).

[Nekama]

Si le problème est "quelle est la vitesse minimale pour que la bille fasse le looping ?" alors oui bien sûr car cette vitesse minimale dépendra de l'altitude à gravir lors du looping et que cette altitude est 2(R-r).

Oui mais :

* la conservation de l'énergie n'est :

ni 1/2 m*v² = 1/2 m*v_f² + m*g (10R) (modélisation ponctuelle)

ni 1/2 m*v² = 1/2 m*v_f² + m*g 2(r-R) (modélisation ponctuelle avec correction de hauteur)

mais 1/2 m*v² = 1/2 m*v_f² + mg 2(r-R)

* Et après un choc, et le rétablissement d'un RSG, on n'a pas :

v_2f² = v_1i² (modélisation ponctuelle)

mais : v_2f² = 25/49 v_1i²

[Black Jack 2]

Le problème vient de l'affirmation que traiter un problème avec une bille ponctuelle (comprendre une boule avec un rayon tendant vers 0) ne permet pas de tirer des conclusions correctes pour une bille non ponctuelle.

C'est cela qui est faux.
Bien entendu, il faut modifier l'énoncé pour en tenir compte, mais c'est une évidence.

Si on a une bille de rayon R et un cerceau de rayon r, le diamètre parcouru dans la boucle par le centre d'inertie de la bille est de 2.(r - R)
Par exemple en numérique, si R = 5 cm et r = 25 cm, le diamètre parcouru dans la boucle par le centre d'inertie de la bille est de 2.(r - R) = 40 cm

Pour avoir des résultats identiques, avec une bille ponctuelle, on devrait prendre un rayon de boucle de 20 cm de manière à avoir des parcours identiques du centre d'inertie des billes dans les 2 exercices.
Ensuite les raisonnements et résultats seront identiques dans les 2 cas.

Dans les 2 cas, on obtiendra des vitesses du centre d'inertie de la bille identiques, des mêmes distances et durées des phases glissement + roulement et pareil pour tous le reste.
Le calcul de la vitesse (en tenant compte de tout) de vo (de l'énoncé initial) sera la même dans les 2 cas si évidemment on impose les même conditions (par exemple que les billes passent en haut de la boucle en roulement sans glissement ... ou bien autre chose, mais identique dans les 2 cas).

[Nekama]

Oui, oui... Ce n'est pas comme si on venait de montrer précisément le contraire à plusieurs endroits.

N'hésite pas à faire les calculs détaillés qui montrent que tu aboutis aux bons résultats avec une approximation ponctuelle d'entrée de jeu.

[Black Jack 2]

Oui, oui... Ce n'est pas comme si on venait de montrer précisément le contraire à plusieurs endroits.

N'hésite pas à faire les calculs détaillés qui montrent que tu aboutis aux bons résultats avec une approximation ponctuelle d'entrée de jeu.

Mauvaise foi ou incompréhension ?

Pour que des problèmes aient les mêmes résultats, il faut évidemment modifier ce qu'il faut (par exemple le rayon de la piste) pour que les centres d'inertie de billes aient des parcours identiques, comme j'en ai donné un exemple dans ma réponse précédente. C'est pourtant élémentaire.

Mais pourquoi ne tentes-tu pas (dans des cas simples pour éviter de te mettre le doigt dans l'oeil) de calculer les différentes formules du message 4.
Avec des billes de masses m , mais l'une avec des rayons de boules de mesure appréciable et l'autre avec des rayons de boules tendant vers 0.
Si les résultats sont identiques (et ils le seront si tu ne te plantes pas), alors ce sera bien parti pour que tu comprennes l'évidence.
Et surtout ne pas ressortir n'importe quoi comme il y aurait une répartition d'énergie différence dans un choc entre 2 boules identiques mais dans un cas avec des rayons R égaux de mesures appréciables ou bien avec les rayons des 2 billes tendant vers 0 (tous les 2 évidemment)

Sur billard (horizontal), une boule de choc animée d'une vitesse vo (roulement sans glissement) entre en collision avec une bille identique immobile (bille choquée), calculer les vitesses de ces 2 boules quand elles finiront (après phase de glissement + roulement après le choc) à une vitesse linéaire stabilisée (il faut évidemment tenir compte du coefficient de glissement dynamique, on se dispense de tenir compte du coefficient de roulement pour faciliter le calculs)

Je te donne les résultats que tu es censé trouver:

Pour la bille choquée : vitesse de roulement stabilisée : 5/7 vo
Pour la bille de choc : vitesse de roulement stabilisée : 2/7 vo (et non cette bille ne reste pas à l'arrêt après le choc)

De nouveau ces résultats sont de nouveau indépendants du rayon des boules (qui doivent cependant être les mêmes pour les 2 boules, mais peuvent parfaitement tendre tous les deux vers 0).

Il y a perte d'énergie (bien que le choc est élastique) à cause du glissement partiel des billes qui suivent le choc.

Aucune des formules nécessaires pour résoudre ce problème ne dépend de la valeur du rayon des billes (qui sont bien entendu identiques si il y a collision).
Comme déjà dit, il faut évidemment que les trajets des centres d'inertie des boules soient identiques ... ce qui n'est pas le cas dans les exemples foireux que tu prétends avoir donné.



Si ce n'est pas encore suffisant pour comprendre, alors ... tant pis

[Nekama]

Hmmm. Sur un forum, c'est bien de lire ce que les autres écrivent :

3. Choc entre 2 billes

Le problème est que quand une bille entrechoque une autre à l'arrêt, la seconde démarre en glissant linéairement et va perdre de l'énergie avant de se mettre à RSG...

Si on étudie la bille percutée :

x'(o) = v_o

mx'' = - µmg et 2/5 m Rph'' = µmg

x' = -µgt + v_o et Rphi' = 5/2 µgt

La vitesse du point de contact au sol vaut :

v_c = x' - R phi' = v_o - 7/2 µgt

v_c = 0 et t_c = 2v_o/7µg

A ce moment :

x' = v_o - µg 2v_o/7µg = 5/7 v_o

Si on veut trouver les vitesses après impact d'un objet RSG de masse M₁, de moment d'inerte I₁ = k₁ M₁R² et de vitesse v_i1 après qu'il ait percuté un objet au repos (ou non) de masse M₂, de moment d'inerte I₂ = k₂ M₂R² (ou d'un autre rayon), et pourquoi pas aussi en prenant en compte également des frottements entre eux, et pas juste une collision, il y a tout intérêt à comprendre comment le calcul se réalise et pas juste être allé lire sur un site quelconque qu'une bille de billard, après avoir été percutée et après avoir repris un RSG aura une vitesse x' = 5/7 v_o. D'autant que ce calcul est tout simple à faire, mais encore faut-il avoir l'humilité de vouloir lire.

[Black Jack 2]

Hmmm. Sur un forum, c'est bien de lire ce que les autres écrivent :



Si on veut trouver les vitesses après impact d'un objet RSG de masse M₁, de moment d'inerte I₁ = k₁ M₁R² et de vitesse v_i1 après qu'il ait percuté un objet au repos (ou non) de masse M₂, de moment d'inerte I₂ = k₂ M₂R² (ou d'un autre rayon), et pourquoi pas aussi en prenant en compte également des frottements entre eux, et pas juste une collision, il y a tout intérêt à comprendre comment le calcul se réalise et pas juste être allé lire sur un site quelconque qu'une bille de billard, après avoir été percutée et après avoir repris un RSG aura une vitesse x' = 5/7 v_o. D'autant que ce calcul est tout simple à faire, mais encore faut-il avoir l'humilité de vouloir lire.

Laisse tomber Nekama, tu mets de l'eau à mon moulin sans même t'en rendre compte.

Penser que je ne peux pas arriver à démontrer ces formules enfantines est risible, cependant tu viens de commencer à démontrer ce que j'affirme depuis le début. On peut parfaitement résoudre le type de problème posé en utilisant le modèle des BOULES ponctuelles (rayon tendant vers 0)

Ici, la vitesse trouvée est la même si on fait le calcul avec des boules de dimensions normales ou bien avec des boules dites ponctuelles.
Et il en serait de même avec toutes les autres "formules" utiles à résoudre le problème posé.

La seule chose à laquelle il faut prendre garde est de conserver dans les 2 énoncés (boules normales ou ponctuelles) un même rayon pour le parcours du centre d'inertie des boules dans la boucle.
Avec des boules "normales", on peut dans certaines "formules" retrouver le terme (r-R) qui n'est rien d'autre que le rayon du cercle parcouru par le centre d'inertie de la boule dans le cerceau. Dans le problème analogue avec des boules ponctuelles, on retrouvera à la place du (R-r) un terme R' qui aura été défini comme rayon du cerceau... mais cela devrait être évident.

Ceci ne veut pas dire que le modèle avec boules ponctuelles doit être privilégié ici, cela signifie simplement que résoudre ce type de problème avec le modèle des boules ponctuelles est tout à fait possible et sans difficultés supplémentaires, contrairement à ce que tu affirmes dans ton message d'origine.

[Nekama]

Non...

Ce que tu affirmes, c'est qu'il y a moyen de faire les calculs plus simplement si on donne à ces boules des propriétés qui "vont bien" (m -> m*).

Sauf que les propriétés des boules ponctuelles que tu veux utiliser (1) changent à chaque nouvelle phase/situation et (2) qu'on ne les connait pas a priori.

Scientifiquement, ce que tu dis, est totalement équivalent à dire que si on connait la réponse, il n'y a aucune raison de la trouver.

Or :

(1)
Il n'y a aucun principe physique général qui dit qu'un problème de billes peut dès le départ se résoudre entièrement en les considérant comme ponctuelles avec une masse donnée.

(2)
Tu connais de mémoire que quand deux billes de même masse s'entrechoquent, la seconde repart à 5/7 vo et la première repart à 2/7 vo.
Tu connais de mémoire les mêmes formules pour des cylindres creux et des cylindres pleins.
Au final, c'est différent que quand 2 particules ponctuelles de même masse s'entrechoquent, où la seconde repart à vo et la première reste immobile.
Si tu ne le connaissais pas de mémoire, tu devrais faire le calcul qui a été fait.

Ta seule motivation quand j'interviens sur ce site est de venir troller mes fils.
C'est ce que tu fais à chaque fois et tu as déjà reçu des remarques pour cela.

Ici tu n'as apporter aucune réponse constructive au problème initial posé, juste affirmer sans le faire qu'on pouvait le faire autrement (et faussement).

[Nekama]

Non...

Ce que tu affirmes, c'est qu'il y a moyen de faire les calculs plus simplement si on donne à ces boules des propriétés qui "vont bien" (m -> m*).

Sauf que les propriétés des boules ponctuelles que tu veux utiliser (1) changent à chaque nouvelle phase/situation et (2) qu'on ne les connait pas a priori.

Scientifiquement, ce que tu dis, est totalement équivalent à dire que si on connait la réponse, il n'y a aucune raison de la trouver.

Or :

(1)
Il n'y a aucun principe physique général qui dit qu'un problème de billes peut dès le départ peut se résoudre entièrement en les considérant comme ponctuelles avec une masse donnée

(2)
Tu connais de mémoire que quand deux billes de même masse s'entrechoquent, le second repart à 5/7 vo et le premier repart à 2/7 vo.
Tu connais de mémoire les mêmes formules pour des cylindres creux et des cylindres pleins.
Au final, c'est différent que quand 2 particules ponctuelles de même masse s'entrechoquent, où la seconde repart à vo et la première reste immobile.
Si tu ne le connaissais pas de mémoire, et il y a autant de cas différents que d'objets de moment d'inertie différent, tu devrais faire le calcul qui a été fait.

Ta seule motivation quand j'interviens sur ce site est de venir troller mes fils.
C'est ce que tu fais à chaque fois et tu as déjà reçu des remarques pour cela.

Ici tu n'as apporté aucune réponse constructive au problème initial posé, juste affirmé, sans le faire, qu'on pouvait le faire autrement (et à tort).

[Black Jack 2]

Non...

Ce que tu affirmes, c'est qu'il y a moyen de faire les calculs plus simplement si on donne à ces boules des propriétés qui "vont bien" (m -> m*).

Sauf que les propriétés des boules ponctuelles que tu veux utiliser (1) changent à chaque nouvelle phase/situation et (2) qu'on ne les connait pas a priori.

Scientifiquement, ce que tu dis, est totalement équivalent à dire que si on connait la réponse, il n'y a aucune raison de la trouver.

Or :

(1)
Il n'y a aucun principe physique général qui dit qu'un problème de billes peut dès le départ peut se résoudre entièrement en les considérant comme ponctuelles avec une masse donnée

(2)
Tu connais de mémoire que quand deux billes de même masse s'entrechoquent, le second repart à 5/7 vo et le premier repart à 2/7 vo.
Tu connais de mémoire les mêmes formules pour des cylindres creux et des cylindres pleins.
Au final, c'est différent que quand 2 particules ponctuelles de même masse s'entrechoquent, où la seconde repart à vo et la première reste immobile.
Si tu ne le connaissais pas de mémoire, et il y a autant de cas différents que d'objets de moment d'inertie différent, tu devrais faire le calcul qui a été fait.

Ta seule motivation quand j'interviens sur ce site est de venir troller mes fils.
C'est ce que tu fais à chaque fois et tu as déjà reçu des remarques pour cela.

Ici tu n'as apporté aucune réponse constructive au problème initial posé, juste affirmé, sans le faire, qu'on pouvait le faire autrement (et à tort).

Le troll n'est pas celui que tu crois.
Tu dis au départ une absurdité, en présentant un type de problème que tu suggères impossible à traiter correctement à partir du modèle de boule ponctuelle.

Je n'écris pas, contrairement à ce que tu affirmes, que ce sujet est plus facile à traiter avec das billes ponctuelles, mais je fais remarquer que ce type de problème peut être traité également correctement avec des boules ponctuelles.

Puis quand on te met, noir sur blanc, quelques formules utiles dans ce genre de problèmes qui montrent clairement qu'elles sont vraies aussi bien avec un modèle de boules normales ou bien de boules ponctuelles, tu ne trouves rien de mieux que d'affirmer que j'ai trouvé ces formules, je ne sais où, mais suis incapable de les démontrer. Non seulement c'est absurde mais sans sujet avec le problème.

Comme tu seras sûr d'avoir raison contre toute évidence, il est inutile de poursuivre notre "débat".

Bonne journée.

[Black Jack 2]

Si le problème est "quelle est la vitesse minimale pour que la bille fasse le looping ?" alors oui bien sûr car cette vitesse minimale dépendra de l'altitude à gravir lors du looping et que cette altitude est 2(R-r).

Bonjour,

Je termine aussi pour toi, pour ne pas te laisser sur les fausses infos que tu aurais pu avoir.

Je te montre comment on peut résoudre le type de problème de ton lien ... même si la bille était ponctuelle.

Résolution du problème de ton lien ... en l'adaptant (comme indiqué dans mes messages précédents) pour le résoudre avec des billes ponctuelles (rayon tendant vers 0) (dessin pour bille ponctuelle en bas)

Dans le problème initial du lien, le rayon du cercle parcouru par le centre d('inertie de la bille dans le cerceau est R-r

Dans le problème avec bille ponctuelle, on aurait donc : R', le rayon du cerceau est tel que R' = (R-r) (1)

Energie mécanique de la bille quand elle passe en haut du cerceau (avec le dessous de la boucle cimme référence des énergie potentielle de pesanteur.

Em = m.g.(ho - 2R')

On a donc en ce point (si la bille roule sans glisser) : m.g.(ho - 2R') = 1/2.m.V² + 1/2.I.w²

pour une bille pleine homogène de rayon r (même si r tend vers 0), on a I.w² = 2/5. m.r² * v²/r² = 2/5 m.v² (même si r tend vers 0, ce qui implique que w tend vers l'oo, cela amène une indétermination facile à lever)

On a donc m.g.(ho - 2R') = 1/2.m.V² + 1/2.2/5 m.v² = 0,7.mv² (avec v la vitesse linéaire de la bille en haut de la boucle)

g.(ho - 2R') = 0,7.v²

v² = g.(ho - 2R')/0,7

Il faut que la réaction normale de la piste sur la piste soir positive et donc : m.v²/R' >= m.g, donc : v² >= g.R'

Ce qui donne g.(ho - 2R')/0,7 >= gR'

ho - 2R' >= 0,7.R'

ho >= 2,7.R'

Ce qui est le même résultat que la résolution avec bille de rayon r donné dans le lien (réponse 2) ... car on a avec (1) : R' = R-r

Attention quand même que ces résolutions (celle du lien et celle ci-dessus) suppose que la bille roule sans glisser sur toute la boucle du looping.
Or ce n'est pas forcément le cas, il manque des précisions sur le coefficient de frottement (en statique) entre la bille et le cerceau pour le savoir.

Pour être complet (dans les 2 résolutions), il faut aussi investiguer pour voir si la bille va faire le tour sans glisser ou non.
Cette étude peut évidemment être faite aussi avec le cas "bille de rayon r" ou bien "bille ponctuelle" (de rayon tendant vers 0)

[Nekama]

Tout ce cinéma pour présenter la même résolution et dire au final la même chose, parce qu'une bille ne peut pas être ponctuelle vu qu'elle roule, et ce quel que soit son rayon R.

La résolution "ponctuelle" à laquelle je faisais référence (et que tout le monde a croisé), est celle de la partie 1 du lien.

Elle consiste à négliger toute rotation çàd de considérer I = 0 et faire comme si l'objet était un point matériel.

Le résultat est bien entendu différent de ceux ci-dessus vu qu'on fait abstraction de tout roulement.

Dans le contexte du point matériel, on a :

1. après collision que v_i = v_o (transfert de toute la quantité de mvt et de toute l'énergie, pas de facteur 5/7)

2. La conservation de l'énergie dans le looping : v_i² = v_f² + 2 g2r

3. La condition pour que le looping est que la force centrifuge soit supérieure à mg : v_f² > gr

Et tout mis ensemble, on obtient : v_o² > 5 gr

ou h = 2,5 r si on résout l'exercice du lien.

---

Cette approximation du point matériel est acceptable si on prend un wagonnet par exemple.

[Black Jack 2]

Si on a une bille, qu'elle soit ou non ponctuelle ... elle peut rouler

Si on veut traiter un problème hors roulement, on doit le préciser dans l'énoncé ... et on ne choisit pas "une bille" comme mobile.
Un énoncé bien fait qui ne veut considérer que le glissement, doit préciser que le mobile glisse.

Cela semble en dépasser certains.

On peut sûrement trouver, sur le net ou ailleurs, des exercices, résolus, qui font la même connerie, soit négliger le fait qu'une bille peut rouler.
Libre à qui le veut de faire la même chose bien que c'est complètement hors réalité.

[Nekama]

Ouais, c'est ça.

Je précise que je NE souhaite PAS traiter d'une bille ponctuelle mais FAIRE AUTRE CHOSE.

Et il y a des gens "suffisamment peu constructifs" pour traiter du sujet qui n'est pas traité : les billes non ponctuelles, à fort recours de dénigrement.

Et ne pas traiter le sujet mais des sujets annexes.

Et j'insiste, ce n'est pas la première fois.