Equations de ligne

[Nekama]

Bonjour,

J'ai un problème (pourtant basique) de lignes mais je ne sais pas comment le résoudre.

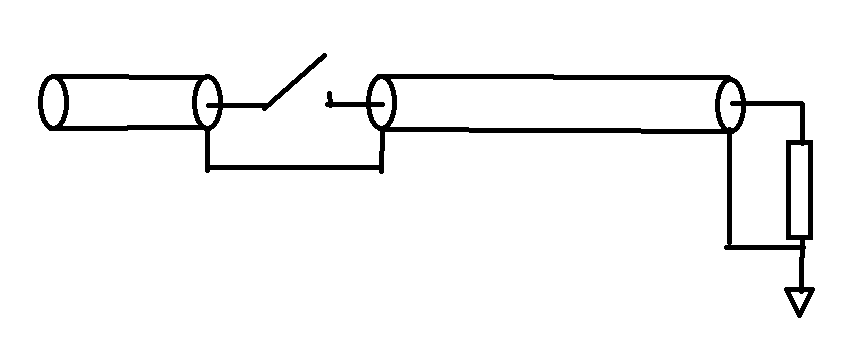
On a en série :
- une ligne de caractéristiques : Zo, t = 1,5 ns (chargée a une tension Uo)
- un switch (ouvert) (monopolaire mais bipolaire ne doit rien changer je pense)
- une ligne de caractéristiques : Zo, t = 5 ns (déchargée)
- en bout de ligne, une résistance R = Zo

Si on ferme le switch, que vaut la tension V_R au cours du temps ?

J'imagine que cela se résout par Laplace ?
Où bien peut-on résoudre cela en raisonnant physiquement par propagation des ondes ?

Merci
-----

[gts2]

Bonjour,

Je dirai, comme tout est à Z0, que Vr voit un échelon V0 décalé de 5 ns.
Mais j'ai peut-être mal compris la question.

[Nekama]

Salut,

Voici un schéma du circuit (pour clarifier).

L'effet de la ligne de transmission de droite n'est pas que de retarder le signal.

Si elle n'est pas présente, on trouve que V_R = Uo/2 ( E(t) - E(t - 3) )
où E(t) est la fonction échelon : E(t) = 1 si t > 0.

Cela s'explique dans ce cas-là par le fait que :
- après la fermeture du switch, le courant circule dans le circuit constitué de Zo + R et la tension V_R - I * R
- l'onde se propage vers la gauche, se réfléchit en t = 1,5 à l'extrémité (- Uo) et en t = 3 est absorbée par la charge qui voit du coup Uo + (-Uo) = 0.

[gts2]

OK compris : en x=0 circuit ouvert, j'avais mis un générateur V0.

[A voir en vidéo sur Futura]

[gts2]

Pour le cas sans deuxième ligne, je vois plutôt (encode une fois si j'ai bien compris) :

V0 statique : somme de deux ondes V0/2 (direct+inverse) chacune de longueur finie 1,5 ns.
Sens direct conduit à V0/2*(E(t)-E(t-1,5))
Sens inverse réflexion avec I=0, donc retour V0/2 conduit à V0/2(E(t-1,5)-E(t-3))
Soit au total un créneau de 3 ns, cohérent avec votre résultat.

Avec deuxième ligne : retarde l'arrivée du créneau de 3ns de 5 ns

[Nekama]

Pour être sur d'avoir compris.

Cas 1.
On scinde Uo en une onde Uo/2 vers la droite et une autre vers la gauche.
Vers la droite, la transmission est totale (rho = 0)
Vers la gauche, il y aura une réflexion totale en bout de ligne qui reviendra donc 3 ns plus tard.

C'est une manière générale de procéder pour gérer une ligne chargée ?

Cas 2.
Ok. Avec le même raisonnement, on trouve bien un créneau de Uo/2 de 3 ns qui arrive après 5 ns.

Cas 3.
Si on reprend le cas 1 avec une alimentation Uo en début de ligne, on ne devrait pas avoir :

Uo/2 pour [5 ; 6,5] et Uo ensuite avec le même raisonnement (?)

[gts2]

C'est une manière générale de procéder pour gérer une ligne chargée ?

C'est ce qui m'est venu comme idée, il faudrait avoir un autre avis.

Cas 3.
Si on reprend le cas 1 avec une alimentation Uo en début de ligne, on ne devrait pas avoir :
Uo/2 pour [5 ; 6,5] et Uo ensuite avec le même raisonnement (?)

Je dirai, Uo/2 pour [5 ; 6,5] puis arrivée de l'onde réfléchie Uo/2 pour [6,5 ; 8], puis l'onde générée par l'alim U0 pour la suite.
(sous confirmation)

[Gwinver]

Bonsoir.
Exercice curieux car il n'y a pas de générateur.

[Nekama]

Je dirai, Uo/2 pour [5 ; 6,5] puis arrivée de l'onde réfléchie Uo/2 pour [6,5 ; 8], puis l'onde générée par l'alim U0 pour la suite.
(sous confirmation)

Une fois que l'onde se réfléchit en t = 1,5 au niveau du générateur, pourquoi l'alimentation tarderait-elle à recharger la ligne ? Et si elle tarde, pourquoi de 1,5 ns ?

Je suis mal à l'aise avec le Uo/2. J'ai l'impression qu'avec deux lignes d'impédances différentes, on n'aurait plus cette équipartition... Mais (?).

[gts2]

Une fois que l'onde se réfléchit en t = 1,5 au niveau du générateur, pourquoi l'alimentation tarderait-elle à recharger la ligne ? Et si elle tarde, pourquoi de 1,5 ns ?

Elle ne tarde pas, elle démarre immédiatement mais il lui faut 1,5 ns pour atteindre R.

Je suis mal à l'aise avec le Uo/2. J'ai l'impression qu'avec deux lignes d'impédances différentes, on n'aurait plus cette équipartition... Mais (?).

Le U0/2 ne concerne que la première ligne : c'est la traduction de l'état initial de celle-ci (v=V0 et i=0 quelque soit x pour t<0)
Si la deuxième ligne est différente, cela fera des réflexions à l'entrée de celles-ci, donc a priori une infinité d'aller-retour qui s'amortiront.

[Nekama]

Elle ne tarde pas, elle démarre immédiatement mais il lui faut 1,5 ns pour atteindre R.

Oui. Evidemment.

Le U0/2 ne concerne que la première ligne : c'est la traduction de l'état initial de celle-ci (v=V0 et i=0 quelque soit x pour t<0)

On pourrait avoir Uo et 0 qui satisfont la condition, soit un échelon +Uo vers la droite et -Uo vers la gauche.

Si la deuxième ligne est différente, cela fera des réflexions à l'entrée de celles-ci, donc a priori une infinité d'aller-retour qui s'amortiront.

Oui. Mais c'est toujours Uo/2 vers la gauche et Uo/2 vers la droite (immédiatement partiellement réfléchi vu les impédances caractéristiques différentes) qui donne le bon résultat ?

[gts2]

On pourrait avoir Uo et 0 qui satisfont la condition.

A préciser : U0+0 satisfait bien mais ne satisfait pas

Traduction graphique de mes messages précédents : ligne6.pdf

[Nekama]

Cristal clear. Merci.

* Uo + E1 + 0 + E2 = Uo + 0 çàd E1 + E2 = 0
* Uo + E1 = 0 + E2

dont la solution est :

E1 = -Uo/2
E2 = Uo/2