Décomposition d'une fonction sur une base

[coussin]

Bonjour,

Je considère une fonction f(x) définie sur un intervalle [a,b].
J'ai également un ensemble de fonctions qui sont orthonormées telles que .

Je cherche à développer ma fonction f(x) sur les comme où les coefficients de développement sont .

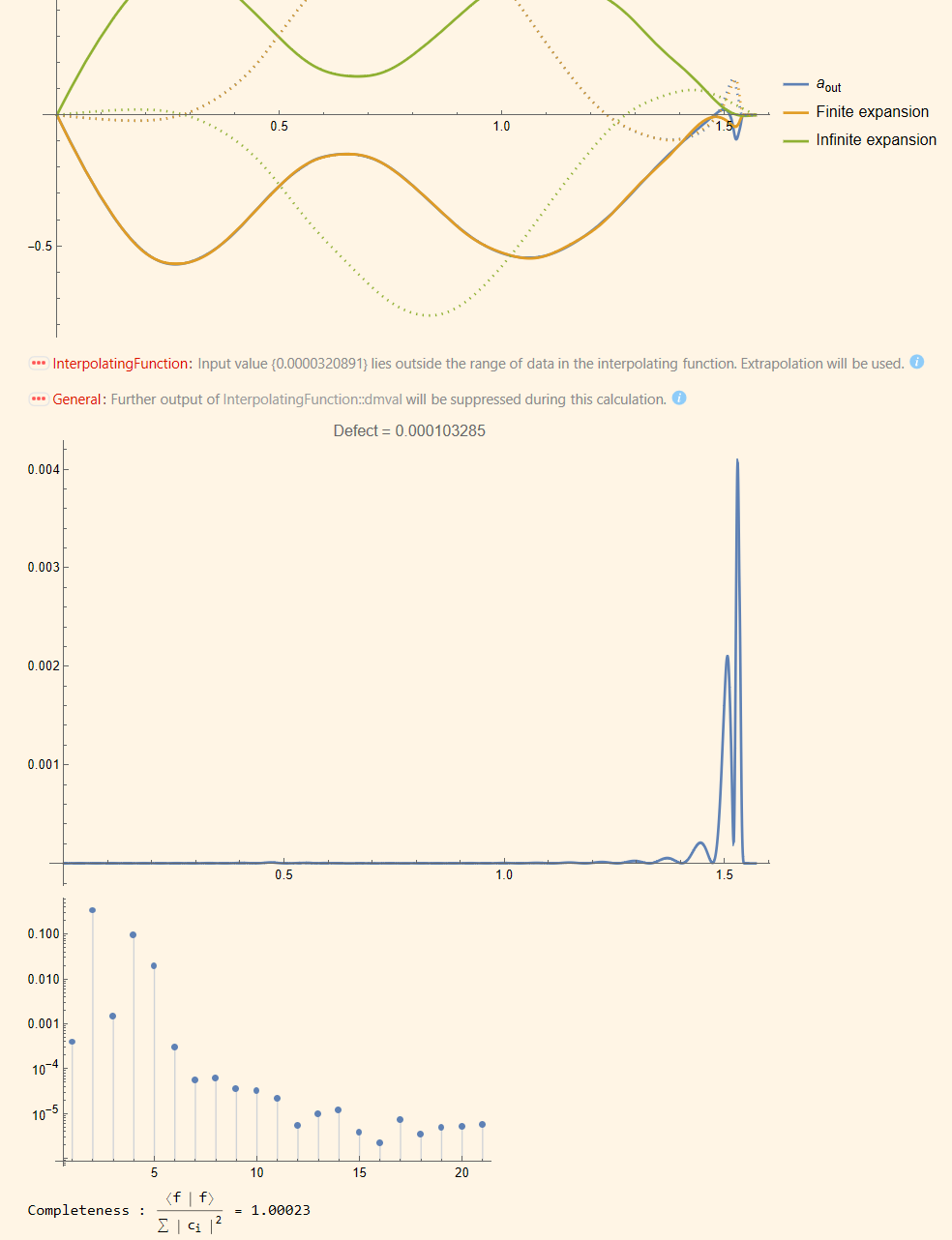
Mon problème est que j'ai un exemple de fonction f(x) qui ne coïncide pas pour tout x à sa décomposition , quel que soit le nombre de termes que j'inclus...

J'en conclus que l'ensemble des ne constitue pas une base des fonctions definies sur [a,b]...

Ma question est alors : quelles propriétés doivent satisfaire un ensemble de fonctions pour être une base sur laquelle je peux développer n'importe quelle fonction f(x) ?
-----

[Anonyme007]

Bonsoir,

Il faut d'abord, voir, dans quel espace de Hilbert vivent tes fonctions. Ensuite, voir si cette famille de fonctions que tu étudies constitue une base Hilbertienne pour cet espace.

Cordialement.

[MissJenny]

n'importe quelle fonction f(x)

il y a des résultats pour certains espaces de fonctions, par exemple les fonctions continues (théorème de Stone Weierstrass notamment) mais pour des fonctions quelconques ça m'étonnerait.

[coussin]

Merci pour vos réponses.

Je pense avoir trouvé ce qui me manque (partiellement), c'est l'indépendance linéaire. En effet, pour former une base, les fonctions doivent être linéairement indépendantes. C'est ça qui donne toute sa flexibilité à la somme .

Ici, la notion d'indépendance linéaire devient locale, à chaque x. On peut comparer 2 fonctions et en calculant leur Wronskien . Si celui-ci est non nul, les fonctions sont linéairement indépendantes et vice versa.
Et effectivement, quand je calcule ce Wronskien pour chaque paires de fonctions , celui-ci s'annule dans une certaine portion de l'intervalle [a,b]. Et c'est dans cette portion de l'intervalle [a,b] que ma fonction f(x) ne coïncide pas avec sa décomposition

[A voir en vidéo sur Futura]

[MissJenny]

l'orthogonalité n'entraîne pas l'indépendance?

sinon on voit facilement qu'il manque des conditions : par exemple tu peux prendre les Phi_i à support sur la moitié de l'intervalle [a, a+(b-a)/2] et orthogonales et il est clair qu'une somme de Phi_i ne dit rien sur ce qui se passe dans l'autre moitié de l'intervalle.

[coussin]

sinon on voit facilement qu'il manque des conditions : par exemple tu peux prendre les Phi_i à support sur la moitié de l'intervalle [a, a+(b-a)/2] et orthogonales et il est clair qu'une somme de Phi_i ne dit rien sur ce qui se passe dans l'autre moitié de l'intervalle.

Exactement. J'avais déjà songé à ce cas de figure (et c'est finalement un peu ce qui se passe dans mon cas...)

Hmmm il faut que j'y réfléchisse plus...
J'utilise une méthode trouvée dans un papier, ce n'est pas de moi
Les ne tombent pas du ciel, elles sont les fonctions propres d'un certain opérateur différentiel.
Je peux citer des passages du papier en question :

[...] For a basis, we take the set of eigenfunctions φk(ρ|θ) of the operator h(ρ) [...]
[...] The operator h(ρ) is Hermitian on the interval [0, π/2] with zero boundary conditions. The set of eigenfunctions is complete, and this permits employing this set as a basis [...]

Ce papier n'est pas en libre accès, je pense que c'est inutile que je donne la référence complète...

[coussin]

Le "problème", je pense, est que en MQ le concept de base complète est défini de manière "moyenne" : le développement ne converge pas vers la fonction de manière ponctuelle, ni même de manière absolue. C'est un critère du type . Ça laisse de la place, localement, à des différences "visibles" entre la fonction et son développement.

Concrètement dans mon cas, j'ai quelque chose comme ça :



Le premier graphe montre la fonction f(x) en trait plein bleue et son développement en trait plein orange. Il y a une différence visible à l'œil vers x=1.5 et cette différence ne change pas en augmentant le nombre de termes dans le développement.
Le deuxième graphe montre la fonction et son intégrale.
Le troisième graphe montre la magnitude des et là, on voit que ça converge pas vraiment... Bon, il peut y avoir plein de raisons numériques pour ça, ça ne me choque pas trop.
Et finalement, le critère de "base complète" qui est au niveau de 1e-4, du même niveau que le défaut calculé au deuxième graphe.

Tout ça est donc "consistant numériquement". Ce qui est un peu étonnant est la différence visible sur le premier graphe qui fait penser à une situation bien pire

[coussin]

En fait, ce que j'ai dit sur la dépendance linéaire doit être vu avec le "flou" du physicien numéricien, pas en termes absolus du mathématicien
Le Wronskien n'est pas exactement zéro, il est juste très petit dans une région autour de x=1.5. Ce qui signifie que, à strictement parler, ma base est effectivement complète mais très dépendante. Il faut probablement un nombre de termes énormes pour faire converger cette région