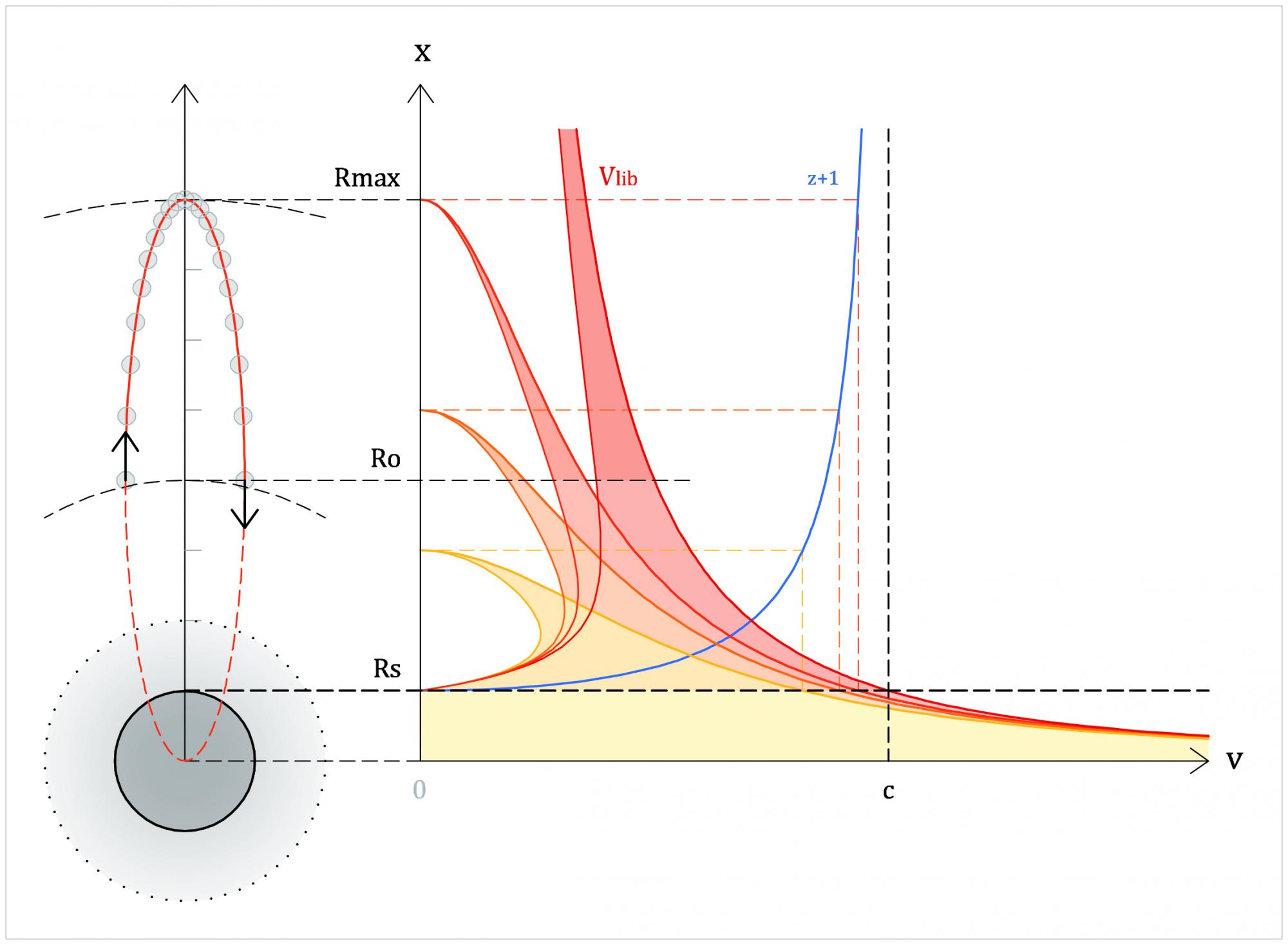
Je veux bien essayer de jouer aux devinettes. Réponse: jamais.Au bout de combien de temps (mesuré par les horloges à r) la métrique, perturbée par l'objet, redevient parfaitement sphérique
La métrique ne l'a jamais été sphérique, elle ne le redeviendras pas.
(Si l'objet qui tombe est suffisamment massif pour amener une dissymétrie mesurable à un quelconque instant, ce sera le cas à tout instant.)
Pour toute question, il y a une réponse simple, évidente, et fausse.
merci pour votre réponse.Envoyé par Amanuensis
ça je le savais, notamment à travers la nature orbites proches, sans matière visible au centre.
je parlais surtout de la nature de ce qu'on appelle "l'horizon".
je ne dit pas brutalement que c'est spéculatif, mais plutôt source de recherche.
Indépendamment de ce à quoi on cherche d'attribuer une date, je ne vois pas l'intérêt de toute cette complication par rapport à parler du temps propre de l'observateur stationnaire, i.e., de la datation qu'il donne normalement à ses observations.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Je ne comprends pas quel type de réponse vous attendez. Quelle nature cela peut-il avoir autre que ce qu'on déduit de sa définition? Pourriez-vous indiquer des réponses qui pourraient être possibles mais dont vcus ne seriez pas sûr?
Dernière modification par Amanuensis ; 22/12/2014 à 19h24.
Pour toute question, il y a une réponse simple, évidente, et fausse.
pas exactement, ma question n'a rien de polémique.
pour ce qui concerne la définition de l'horizon, elle n'est déjà pas très claire ( physiquement ) pour moi.
et pour ce qui se passe au "franchissement" , il me semble que chacun y va de son propre avis.
donc je me sens dans un topic qui est plus proche de la recherche que de la vulgarisation scientifique parfois.
c'est juste une remarque.
cela reste très intéressant.
Voilà celle qui est claire pour moi (mais peut-être incorrecte), en deux étapes:
1) surface séparant les événements tels qu'il existe au moins une ligne d'Univers passant par l'événement et traversant dans le futur de l'événement la surface (intérieur), et ceux tels qu'il n'existe pas de telle ligne (extérieur).
Cette définition est valable pour n'importe quel cône futur.
2) horizon d'un trou noir (en RG pure): toutes les lignes passant par un événement intérieur finissent à une singularité de courbure en durée propre finie.
Sûr qu'il est préférable de prendre une discussion sur des théories physiques parfaitement mathématisées (1) pour un débat d'opinion. Cela rend la discussion plus ouverte et plus vivante.et pour ce qui se passe au "franchissement" , il me semble que chacun y va de son propre avis.
(1) Je parle là de ce qu'on peut discuter avec la RG "pure", sans chercher à rajouter des rideaux de fumée tirés de la MQ ou d'autres choses.
Dernière modification par Amanuensis ; 22/12/2014 à 19h58.
Pour toute question, il y a une réponse simple, évidente, et fausse.
merci beaucoup pour votre réponse.
mais vous parlez de "singularité" , ce qui semble géner pas mal de physiciens.
maintenant j'arretes mon HS. car vos discussions sont plus enrichissantes.
Bonsoir je voudrais avoir des précisions sur le point (2).
La durée propre de parcours pour l'observateur en chute libre depuis Ro jusqu'à la singularité est finie certe, mais la formule
qui donne une vitesse <c pour r < Rs devient supraluminique selon l'altitude de départ.
les courbes à droite qui deviennent supraluminiques sont
celle de gauche convergeant vers 0 au niveau de Rs sont
Cordialement,
Zefram
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
J'aurais plutôt dit* Si jamais, (le champs gravitationnel reste éternellement perturbé et non sphérique, du côté où l'objet a été envoyé), alors le modèle de l'"étoile gelée" ou le modèle du TN classique sont possibles (d'où le côté indiscernable des deux modèles). Et je pense que ce serait le résultat expérimental.
* Si au bout d'un certain temps, la question est : combien de temps ?
* Si jamais => étoile gelée
* Si au bout d'un certain temps => TN classique
en une durée finie dans leur temps propre
Un espace propre permet de mesurer : coordonnées spatiales (positions/lieux) -> distance-coordonnées (intervalle de positions)
Un temps propre permet de mesurer : coordonnées temporelles (dates/heures) -> durée-coordonnées (intervalle de dates)
Dernière modification par Nicophil ; 23/12/2014 à 00h09.
La réalité, c'est ce qui reste quand on cesse de croire à la matrice logicielle.
Salut,
Pourquoi ne peut on affirmer que lorsqu'on ne reçoit plus de signal d'état d'avant franchissement , c'est que le franchissement est en cours ou bien fini ? Uniquement parce que l'objet n'est déjà plus visible ( doppler ) avant ?
désolé si c'est trop trivial
Oui, c'est pourquoi je précise "RG pure" ; cette singularité n'est "que" un résultat mathématique, une propriété du modèle. Il y a d'autres possibilités de modèles, qui évitent la singularité. Non seulement en invoquant la physique quantique, mais même d'autres géométrisations de l'espace-temps qu'il est impossible pour le moment de distinguer expérimentalement et/ou par observations de la "RG pure".
Ceci dit, cela ne change pas grand chose à l'idée de trou noir, il me semble. Peut-être (je m'aventure) il est suffisant de remplacer "atteindre la singularité" par "atteindre un événement où la densité d'énergie-impulsion dépasse tel seuil", ou "où tel invariant de courbure dépasse tel seuil" pour garder une définition opérationnelle évitant toute référence à une singularité.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Utiliser un autre système de coordonnées. On ne prépare pas une mission en Antarctique avec une carte de Mercator. Et encore moins avec une projection stéréographique centrée sur le pôle nord.
Dernière modification par Amanuensis ; 23/12/2014 à 06h53.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Mais le théorème de calvitie ne dit-il pas que le métrique devrait redevenir parfaitement sphérique ? Ca c'est un point important. Pensez-vous que le th. de calvitie n'est pas valable, ou, comme moi, que le théorème de calvitie est valable à TSw = infini ?
Oui, mais leur temps propre est le temps de Swarzchild, celui de la métrique, qui est calculé infini selon la métrique. Donc, pourquoi fini dans le temps de Swarz. ? Quelle formule ou quelle logique donne ce résultat ?
D'accord. C'est pourquoi que n'ai pas compris pourquoi vous parliez de "devinette" au post #151. Pourquoi qualifier de "devinette" un problème clairement posé, avec un dispositif expérimental clair, résolu dans une des théories physiques parfaitement mathématisées ?
Je ne comprends pas, le temps propre est le temps
Dans la version d'origine il n'était certainement pas bien posé. Mais même avec quelques corrections élémentaires, il n'est pas bien posé. Facile: bien posé = en langage mathématique, dans le cadre de la théorie parfaitement mathématisée.
Le point principal qui me gêne est l'hypothèse sous-jacente que je crois deviner, qui est que la métrique serait "de symétrie sphérique" initialement (à cause du "revenir..."). Elle ne peut pas l'être avec une masse rajoutée, on ne peut pas mathématiser la création d'une énergi-impulsion ex-nihilo (il y a des contraintes de conservation dans les équations de la RG). Peut-être pourrait-elle l'être dans un certain ouvert incluant au moins l'horizon et son intérieur? Je ne sais pas, mais il y a un point à clarifier, suffisamment à lui tout seul à refuser le label "bien posé".
Et il y a d'autres remarques allant contre "clairement posé, avec un dispositif expérimental clair, résolu dans une des théories physiques parfaitement mathématisées".
(Par ailleurs, en RG les équations sont très très très rarement résolubles par d'autres moyens que des calculs massifs. Ce qui rend l'intérêt de ce genre d'expérience de pensée très limité. Soit on reste à des généralités "élémentaires", des propriétés aisément dérivées du modèle, soit la question, même "bien posé", sera une devinette, ouverte à supputations en l'absence de moyens adaptés.)
Pour toute question, il y a une réponse simple, évidente, et fausse.
Le temps "t" de la MdS est le temps de Minkowski à l'infini, qui est le temps propre tau de quelqu'un qui se situe à r=infini. dt/dtau=1 à l'infini, et dt=dtau=infini à Rs.C'est t qui vaut l'infini pour le passage de Rs, pas
Ce qui est bien avec quelqu'un à l'infini, c'est qu'il n'observe rien du tout, aucun signal venant d'un point fini n'ayant eu le temps de l'atteindre.
(Pas vraiment une boutade, cela explique pourquoi dans un diagramme de Penrose les infinis spatiaux sont asymptotiquement sur un point unique, avec un cône passé asymptotiquement vide (et un cône futur vide, pareil.)
---
Au-delà de la boutade, la définition proposée offre nombre de difficultés, l'une étant la trajectoire et la 4-vitesse d'un tel observateur. Clairement celle-ci ne peut être quelconque, cela donnerait un "temps" quelconque.
Dernière modification par Amanuensis ; 23/12/2014 à 17h02.
Pour toute question, il y a une réponse simple, évidente, et fausse.
: d'accord, t est le temps tau de quelqu'un, pas le temps tau qui intervient dans la métrique.
: d'accord, si l'infini signifie r = infini et dtau = dtau de la métrique.
: si dtau = dtau de la métrique, moi pas comprendre, la métrique ne dit pas cela.
Enfin, il me semble.
Je ne demande pas mieux que d'améliorer la description de l'expérience de pensée du post #143 (qui est fondé sur la "machine" de Wheeler/Thorne pour positionner et définir les horloges). Cela s'est bcp amélioré depuis le départ, les OG, douteuses, sont évitées, et on ne parle que de relations causales et pas de simultanéité ou même avant/après. Que pensez-vous de reformuler ainsi :
"Au bout de combien de temps (mesuré par les horloges à r) la métrique, perturbée par l'objet, devientparfaitement sphérique, signe que le TN l'a absorbé et restitue un aspect sans poils ?"
Le fond de l'expérience n'est pas changé si on suppose ou non que la symétrie est parfaitement sphérique au début. Le fond de l'expérience est de définir un temps T, lié causalement à l'événement : le TN a "absorbé" l'objet. Et le fait (par le th. de la calvitie) que la métrique devient parfaitement Schwarzchildienne qui permet (en principe) de définir ce temps T, que celle-ci soit Schw au début ou non.
Quant à la complexité de résolution, on se place dans la métrique de Schw, qui est la plus simple qu'il est possible d'avoir en RG (même si elle est perturbée par l'objet nous sommes d'accord, mais on suppose que la masse de l'objet est très faible devant celle du TN, et que la métrique est quasi-Schw).
Typo, lapsus clavier, je voulais dire dt/dtau pas dt=dtau: si dtau = dtau de la métrique, moi pas comprendre, la métrique ne dit pas cela.
Enfin, il me semble.
C'est bien pour cela que, dans l'expérience de pensée, on ne se place pas à l'infini mais à distance finie du TN, avec des horloges synchronisées sur le temps de Minkowski par le dispositif de Thorne/Wheeler. C'est une des raisons de la "complication" que vous releviez.
Dernière modification par Urgon ; 23/12/2014 à 17h12.
En fait la définition de t la plus rigoureuse est simplement la coordonnée temporelle de l'espace-temps décrit par Schwarzschild. On la construit à partir des hypothèses (vide, symétrie sphérique), à partir desquelles on démontre qu'on peut choisir une coordonnée temporelle telle que l'expression de la métrique ne dépende pas de la coordonnée temporelle. (La démo de la construction de la solution de Schw. est aisément trouvable dans des cours.)
C'est ensuite qu'on montre que la coordonnée t est asymptotiquement proche du temps propre pour des trajectoires immobiles quand r tend vers l'infini. Et t n'est le temps propre d'aucun observateur, juste une approximation d'autant meilleure que r est grand.
Mais c'est une propriété secondaire: celle importante est que la coordonnée t a été choisie pour que la forme métrique ait une forme indépendante de t.
(Et plutôt que l'appeler "temps de Minkowski", cela me paraîtrait plus parlant de parler de "temps de Schwarzschild"!)
Dernière modification par Amanuensis ; 23/12/2014 à 17h27.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Mon point n'était pas là. Il était pourquoi s'encombrer de la coordonnée de Schwarzschild alors que la description de l'expérience avec le temps propre de l'observateur semble ne rien changer au fond de la question.
Il me semble que la complication en question est inutile pour le propos de l'expérience décrite.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Reste plein de problèmes.
Comment détermine-t-on la symétrie de la métrique, comment cela est-il défini?
Les observateurs sur le cercle ne peuvent pas mesurer grand chose, et certainement pas la "métrique" de tout l'espace-temps. La symétrie en question est posée comme hypothèse dans la construction de Schw., ce n'est pas quelque chose de mesuré ou constaté.
Les observateurs sur le cercle peuvent comparer leurs observations, et déterminer si, du moins pour ces aspects là, ils sont "symétriques". Bien plus réduit que la métrique, mais cela fait peut-être l'affaire?
Quelles observations peuvent-ils comparer pour déterminer la date à laquelle ils (les observateurs) sont "redevenus symétriques"?
En d'autres termes, travailler sur la base de petites perturbations relativement à la solution de Schw., c'est à dire (en gros) négliger le second ordre.Quant à la complexité de résolution, on se place dans la métrique de Schw, qui est la plus simple qu'il est possible d'avoir en RG (même si elle est perturbée par l'objet nous sommes d'accord, mais on suppose que la masse de l'objet est très faible devant celle du TN, et que la métrique est quasi-Schw).
Pour toute question, il y a une réponse simple, évidente, et fausse.
Mais je ne pense pas que raffiner la description changera grand chose à la réponse, qui doit être "jamais".
Et ce juste en se basant sur des règles causales simples, déduites de propriétés générales du modèle mathématique. À ce stade, il est difficile de comprendre pourquoi ces règles générales ne sont pas applicables.
Et en l'espèce c'est juste la causalité: le cône futur de tout franchissement de l'horizon a une intersection vide avec l'extérieur de l'horizon, par définition même de l'horizon. Un chemin causal quelconque, au sens d'une tangente de norme carrée jamais spatiale, aussi tordu soit-il, allant du franchissement aux observateurs à r fixe serait en contradiction avec cette propriété.
Qu'invoquer alors pour opposer la réponse "jamais"? Que la définition de l'horizon est fausse? Qu'il y a deux définitions distinctes pour "horizon", l'une ayant la propriété l'autre non? L'existence de chemin causaux avec une autre définition?
Je ne vois pas de possibilité qui ne serait pas contradictoire avec le cadre mathématique choisi, mais je suis intéressé par les propositions.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Bonsoir, je n'ai pas compris tout, mais j'ai une question : d'aprèshttp://fr.wikipedia.org/wiki/Sph%C3%A8re_de_photonsUne sphère de photons1,2 ou sphère photonique3,4 est, en astrophysique, une surface définie comme l'ensemble des points d'où un photon, particule élémentaire associée aux ondes électromagnétiques, peut être émis et suivre une orbite fermée et périodique.
ethttp://fr.wikipedia.org/wiki/Univers_de_G%C3%B6delLes lignes de coordonnées de
est ce que la sphère photonique est la limite de l'univers de Gödel, càd les courbes de genre temps fermées sont les orbites fermées et périodiques de la sphère photonique?
On utikise la métrique de Gödel pour décrire l'intérieur du TN .
