Le défaut provient probablement de l'utilisation des plans de simultanéité, cette construction serte à évaluer des mesures et uniquement pour un repère inertiel. j'insiste sur le fait qu'un plan de simultanéité est un outil de calcul uniquement, il ne reflète pas la réalité physique.
Ce n'est en aucun cas ce que peut voir un observateur, et surtout un observateur accéléré, il faut se servir uniquement du cône de visibilité du passé, pour décrire ce que voit un observateur.
Comprendre c'est être capable de faire.
La figure semble correspondre à un amas d'étoiles que le voyageur laisserait loin derrière loin, mais pas à un amas d'étoiles qu'il traverse, il me semble aussi que le report vers l'avant est trop faible pour une vitesse de 0,943 c, presque tout devrait être reporté vers l'avant ?Envoyé par Zefram Cochrane
Comprendre c'est être capable de faire.
Bonsoir,
J'ai modifié le schéma pour m'assurer de la justesse des calculs suite à ta remarque.
Lorsque l'observateur atteint la vitesse de 0.943c en accélérant à g° =10m/s² depuis le centre du cercle vert, il aura parcouru 60 000 000s.l ( mesuré depuis son référentiel de départ) et atteint la circonférence du plus grand cercle (360 points au lieu de 36).
J'ai représenté différent secteurs de couleur pour y représenté le redschift: blueschift
secteur rouge de 0.17 à 1/3
ligne orange 1/Cosh(eta) = 1/3.
secteur jaune de 1/3 à 1
ligne verte =1
secteur cyan 1 à 3
ligne Bleu=3
secteur violet de 3 à 5.80.
Je pense que ta remarque sur la déportation à l'avant est du au fait qu'on représente rarement sur les schémas la ligne verte mais plutôt la ligne bleue qui doit être plus conforme à ton intuition.
Sur la vidéo d'Alain Bernard, il obtient me semble t'il les même résultats que moi qui me base sur ce que voit l'observateur donc sur le cône de lumière passé; c'est l'équivalent je crois de la projection qu'il fait dans la vidéo.
Pour la fin sur la vidéo, il sort de l'amas globulaire, d'où le trou tandis que sur mon schéma, mon observateur se trouve à la périphérie et il voit bien un trou devant lui puisque les premières étoiles bleues dans le champ de vision de l'observateur sont séparées d'une courte distance.
On voit aussi sur le schéma les étoiles s'accumuler vers l'arrière et le centre de chaque cercle d'étoiles qui correspond à la position apparente du point de départ de l'observateur tendre à s'écraser contre la position apparente de l'horizon de Rindler situé à une distance apparente de Rh/2 de l'observateur
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Waou c'est quoi ce bombardement de graph ? J'ai pas le temps de suivre...
Ok pour le dernier a condition qu'on soit au bord du cercle (comme dit par phys4 l'obs ne peut pas etre au centre, mais tu as corrigé).
Avant dernier rien compris, a nouveau c'est trop obscur, unités etc...
Pour le 105 je suis a la bourre mais il semblerait que tu aies raison, au moins partiellement vu que j'ai pas fini...
A bientot, et fais une pause stp je tiens pas le rythme
Trollus vulgaris
Merci pour le détail, j'ai repris ces valeurs et utiliser les tableaux que j'avais fait pour Mailou dans le temps.
On retrouve le trou avant qui est un cône d'angle au sommet 19,2°, il correspond au fait que l'observateur sort de la sphère d'étoiles, en mécanique classique, tout le demi espace avant serait vide.
Le shit change sur le cône à 45°, et fait remarquable, cette limite est celle du cône arrière à 45° dans le référentiel de départ, donc la moitié de la sphère est en blueshift et l'autre moitié en redshift
Ce qui me rassure c'est que le trou avant et uniquement du la position arrière de la sphère d'étoiles isotrope autour du point de départ. Il n'existerait pas dans un espace rempli régulièrement d'étoiles, la moitié du champ d'étoiles se trouverait dans le cone avant de 19,2°. Je trouve que ce choix particulier de distribution d'étoiles n'est pas clairement expliqué dans la vidéo.
Comprendre c'est être capable de faire.
Certes mais hors sujet
Bonjour,
Pour l'avant dernier je ne sais pas si tu parles du 120 ou du 118?
Pour le 120 c'est comme le 123 sauf que les couleurs servent uniquement à indentifier les cercles concentriques par incrémentation du rayon de 5000 000s.l dans le repère de la station et que l'observateur voie en atteingant 0.943c.
Ok pour la pause.
J'ai un autre schéma sous le coude montrant, sembleriat -il la nature hyperbolique de l'horizon de Rindler.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Bah vas y on est plus à ca près... met qq unités ca peut aider à lire.
Pour ma part je cherche une methode simple (et graphique) pour donner rapidement le resultat et je n'ai trouvé que pour une serie de points. Comme je n'ai pas envie de passer par les formules, si je ne trouve pas ma methode ca va etre looong, snif. Je link des que c'est pret mais j'ai bcp de mal a evaluer quand..
A plus
Mailou
Trollus vulgaris
Alors rien ? snif
Perso j'ai trouvé ma methode graphique pour ce qui est vu par l'accéléré, yapuka... trouver le temps, car c'est le plus gros du problème
Trollus vulgaris
Salut.
es tu raccord avec moi au niveau des calculs?
La vitesse atteinte par l'observateur (flèche noire) est de V=0.999 999c.
la figure semble indiquer que les points de part et d'autre de l'horzon de Rindler (pioint Vertà gauche) se concentrent sur une courbe projetée vers l'avant de l'observateur à cause de l'aberration de la lumère.
Au fur et à mesure que la vitesse de l'observateur s'approche de celle de la vitesse de la lumière, le redschift remonte la courbe. le point vert à droite donne la distance parcourue depuis qu'il a accéléré (c'est juste pour donner un ordre d'idée).
il faut que je fasse un autre schéma mais avec des cercles concentriques centrés sur le plan perpendiculaire à la trajectoire de l'obsrvateur car c'est ce qui est le plus pertinert.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
Ca a l'air oui, meme la trajectoire "brisée" qui me piquait les yeux ! j'en suis à 2 sur 4 (objets) et une grosse flemme
Rien compris ! Si tu commencais par ce que ca represente avant les conclusions ?La vitesse atteinte par l'observateur (flèche noire) est de V=0.999 999c.
la figure semble indiquer que (...)
C'est la facon dont le point vert de droite voit les cercles colorés alors qu'il va a 0.99...c ? Alors c'est normal que la figure tende vers une parabole il me semble (section de cone par un plan quasi-parallele au cone, le plan etant reciproquement la trajectoire d'une droite, faite de cercles, coupant le cone).
Dernière modification par Mailou75 ; 23/10/2017 à 23h04.
Trollus vulgaris
Salut,
J'ai fait un autre schéma:
sur ce schéma, Vert (point vert cercle noir) accélère à T=0s à g°=c/Rh (Rh exprimé en s.l) la station (point vert cercle rouge) se trouve une distance Rh de Vert. J'ai représenté une série de cercles ( le choix de mettre le centre des cercles sur l'axe vertical de Vert à son point de départ est motivé par le schéma du message http://forums.futura-sciences.com/as...ctoires-8.html) et j'ai voulu savoir comme Vert les percevraient en atteignant une vitesse de 0.999 999 999c.
Comme prévu les points se concentrent sur une ligne dont l'axe directeur est la verticale. On remarque également que que Vert ne verra derrière lui que les points situés initialement à une distance verticale inférieure à Rh de lui.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
Pas vraiment plus clair... pour une vitesse precise ce n'est que de l'aberation semblable a un MRU à 0.999...c, je ne vois pas le rapport avec Rindler, et encore moins avec le fil...
Stp, decris simplement ce que tu representes avant les conclusions : Là je vois plein de cercles verts et une parabole rouge en points... le lien n'est pas direct.
Merci
Trollus vulgaris
Salut,
Si ton horizon de rindler se trouve à 30 000 000s.l à l'aval de la trajectoire. On peut se demander comment l'observateur qui accélère va percevoir son environnement et notemment la partie se trouvant derrière l'horizon de Rindler lorsqu'il atteind une vitesse proche de c; c'est ce que représente partiellement mon dernier schéma. La réponse est que l'environnement de l'observateur semblera se concentrer sur la courbe qui apparait en rouge avec un fort redschift.
Pour donner un ordre d'idée la distance parcourue lorsqu'il atteint V=.999 999 999c par l'observateur est de plus de 6600 parsecs alors qu'initialement les points du plus grand cercle sont éloignés de l'observateur de 2,7 parsecs.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
Si je ne prend que le premier cercle vert autour du point noir (observateur) alors celui ci ne peut etre vu comme une "ligne", quelle que soit sa forme. Ce qui est devant est vu devant et ce qui est derriere est vu derriere, malgré toutes les distorsions possibles ceci reste obligatoire. Le probleme c'est peut etre de commencer par 0,999.999.999c, pour la comprehension ca n'aide pas... essaye 0,8c ?
+ c'est de l'aberration à 0,999...c quel rapport avec l'acceleration ?
A+
Trollus vulgaris
Salut,
Pour clarifier pourquoi tu avais raison
On a trois étapes du voyage de notre observateur accéléré (Noir) :
- T=0 (espace noir) Départ, il voit le passé
- T=18s (vert foncé) en plein élan... juste avant de croiser Bleu clair
- T=28s (vert clair) "Arrivée", il croise Bleu foncé et continue d'accélérer
Les trois Minkowski montrent dans quel référentiel il se trouve et comment le cône passé (jaune) doit être projeté sur l'espace euclidien (droites noire/vertes). On peut donc obtenir ton graph, ce qui est vu, en faisant autant de changement de repère qu'il y a d'images. J'ai représenté comme toujours les battements de secondes de chacun (enfin secondes si on prend a=0.05c/s, sinon une autre unité).
La superposition ou le décalage vertical des images traduit le blue/redshift (z+1) et l'allongement/compression horizontale traduit l'aberration (z+1, aussi). J'ai négligé l'effet "banane/œuf", négligeable... on est dans le symbolique. On confirme que Noir ne verra jamais Rouge au départ (T=0), pas plus que Orange à (T=10s) etc, l'Horizon de Rindler.
Noir voit bien Bleu foncé s'éloigner au départ (!!) et Rouge se rapprocher indéfiniment d'une asymptote (à 10sl non représenté), toutes mes confuses
Les flèches grises devraient être numérotées de 0.1c à 0.9c, j'ai épuré. On voit aussi que Noir commence à voir Bleu se rapprocher à partir du moment où voit l'évènement "départ T=0" de Bleu : rayon lumineux pointillé (j'avais un tout petit peu raison, lol)
NB : Bleu clair et Bleu foncé n'ont pas distance "juste" : 9,.. et 21,.. pour m'approcher de ta description en ayant des temps propres ~ronds, comme d'hab.
Merci pour les critiques
Mailou
Dernière modification par Mailou75 ; 29/10/2017 à 23h50.
Trollus vulgaris
Salut Mailou,
merci pour ces schémas. Je me demande ce que sa donnerait si à T=0s Orange et les Bleus accélèrent à c²/g à T=0s?
Our répondre à ta question, si après avoir atteint V=0.8c l'observateur cesse sont accélération, tous les points finirait par se retrouver derrière l'observateur et s'éloigneraient de lui à une vitesse apparente de c/2.
Mais si l'observateur maintient son accélération, l'horizon de Rindler perdure et les points s'aglutinnent le long d'une courbe ( hyperbolique?)
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut Zef,
De rien, merci à toi
Tu veux dire des accélérés "de Rindler" (dont l'acceleration est inversement proportionnelle à la distance à l'horizon) ou des trajectoires "parallèles" (genre dessin de droite ici http://forums.futura-sciences.com/as...ml#post5997984) ?
Merci pour le nouveau schema, on voit mieux ce que tu es en train de faire, tout n'est pas superposé sur une courbe. Mais je ne comprend toujours pas... grrr. Peux tu decrire tres simplement ce qui est dessiné ? Car je ne reconnais pas l'aberration a 0,8c, pas plus que l'hyperbole à 0,9999..c qui devrait etre une droite tellement c'est plat, ni pourquoi l'obervateur (si c'est le point noir) est dans le petit cercle et le voit pourtant entierement derriere lui. Peut etre est ce l'intervention de l'acceleration mais je ne vois pas bien pourquoi, elle n'est qu'un changement de repere progressif !?Pour répondre à ta question, si après avoir atteint V=0.8c l'observateur cesse sont accélération, tous les points finirait par se retrouver derrière l'observateur et s'éloigneraient de lui à une vitesse apparente de c/2.
Mais si l'observateur maintient son accélération, l'horizon de Rindler perdure et les points s'aglutinnent le long d'une courbe ( hyperbolique?)
Et pourrait on avoir le Minko de ce que tu decris avec la "vitesse apparente c/2"? Je ne comprend pas bien l'histoire, alors qu'un petit Minko peut mettre tout le monde d'accord
Merci
Mailou
PS : Dans le schéma du message 136, le dernier, trouvez l'erreur !! Repetée dans les 4 dessins.
Un indice : le mec ne sait pas compter... (30-3=?)
PS2 : Et quand je regarde ces dessins cote a cote je me demande bien ce que signifie "vitesse lumiere" a part "intervalle d'espace temps nul". Plus ça va moins je digere cette histoire de photon qui voyage...
Trollus vulgaris
oui c'est ça.Salut Zef,
De rien, merci à toi
Tu veux dire des accélérés "de Rindler" (dont l'acceleration est inversement proportionnelle à la distance à l'horizon) ou des trajectoires "parallèles" (genre dessin de droite ici http://forums.futura-sciences.com/as...ml#post5997984) ?
effectivement, il ne devait pas voir le petit cercle entièrement derrière lui puisque lorsqu'il commence à accélérer à g°=10m/s², l'observateur se trouve au centre du petit cercle vert qui mesure 30 000 000s.l de rayon et lorsqu'il atteint 0.8c , il se sera éloigné de 20 000 000s.l de sa postition initiale .
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Je te demande si c'est A ou B, tu me reponds "oui c'est ça"...
Donc c'est ce qui est vu quand il atteint 0,8c ? Mais je ne comprend toujours pas pour l'accélération.. elle n'est là que pour l'histoire qui amene un observateur à cet evenement et cette vitesse relative, ensuite c'est un sujet d'aberration, pas d'acceleration, ca serait bien de ne pas tout mélanger. Et puisque c'est de l'aberration, je ne comprend pas pourquoi le petit cercle a (toujours) une forme de haricot ? Bref, un petit Minko vaut mieux qu'un long dicours...effectivement, il ne devait pas voir le petit cercle entièrement derrière lui puisque lorsqu'il commence à accélérer à g°=10m/s², l'observateur se trouve au centre du petit cercle vert qui mesure 30 000 000s.l de rayon et lorsqu'il atteint 0.8c , il se sera éloigné de 20 000 000s.l de sa postition initiale .
Trollus vulgaris
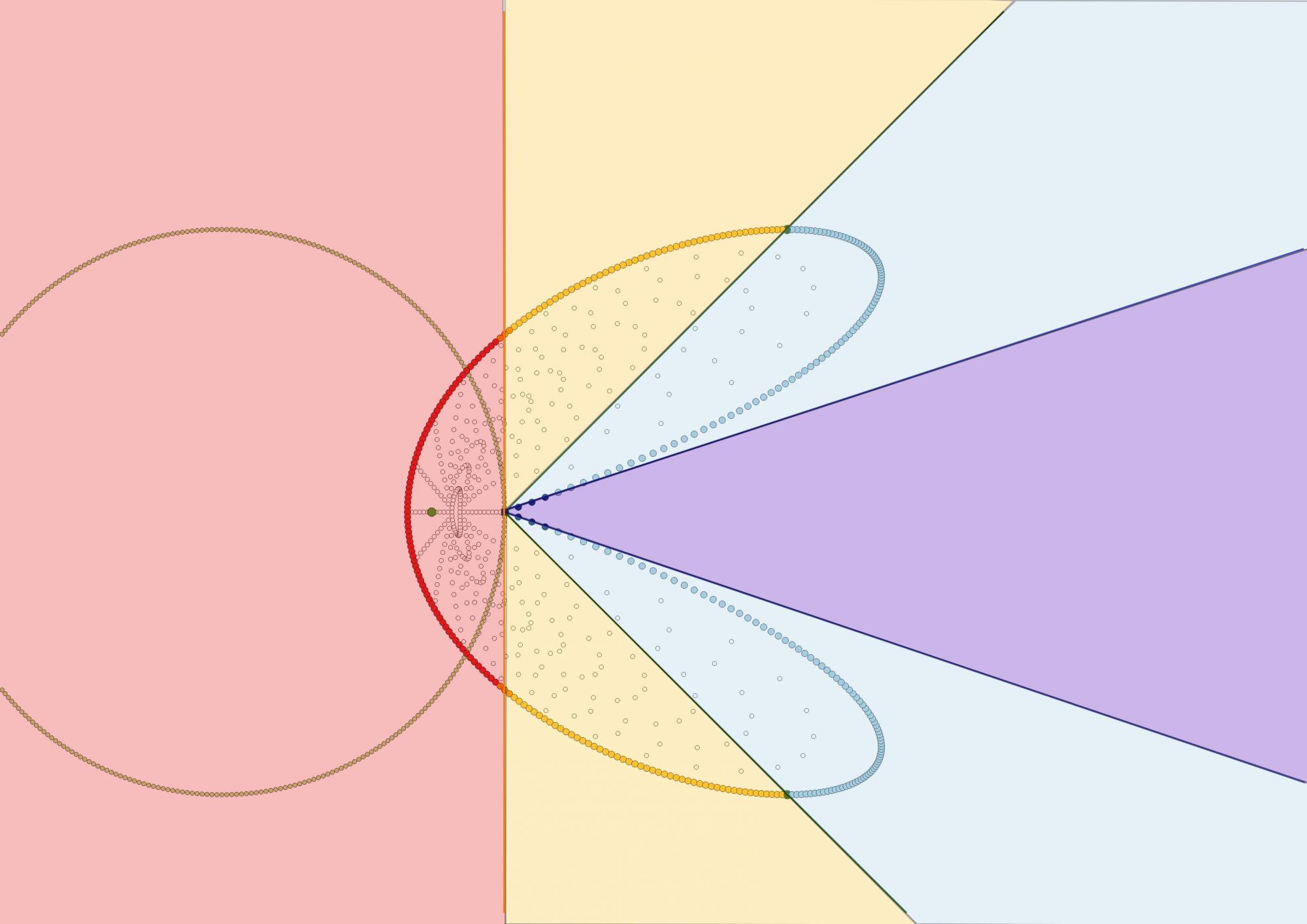
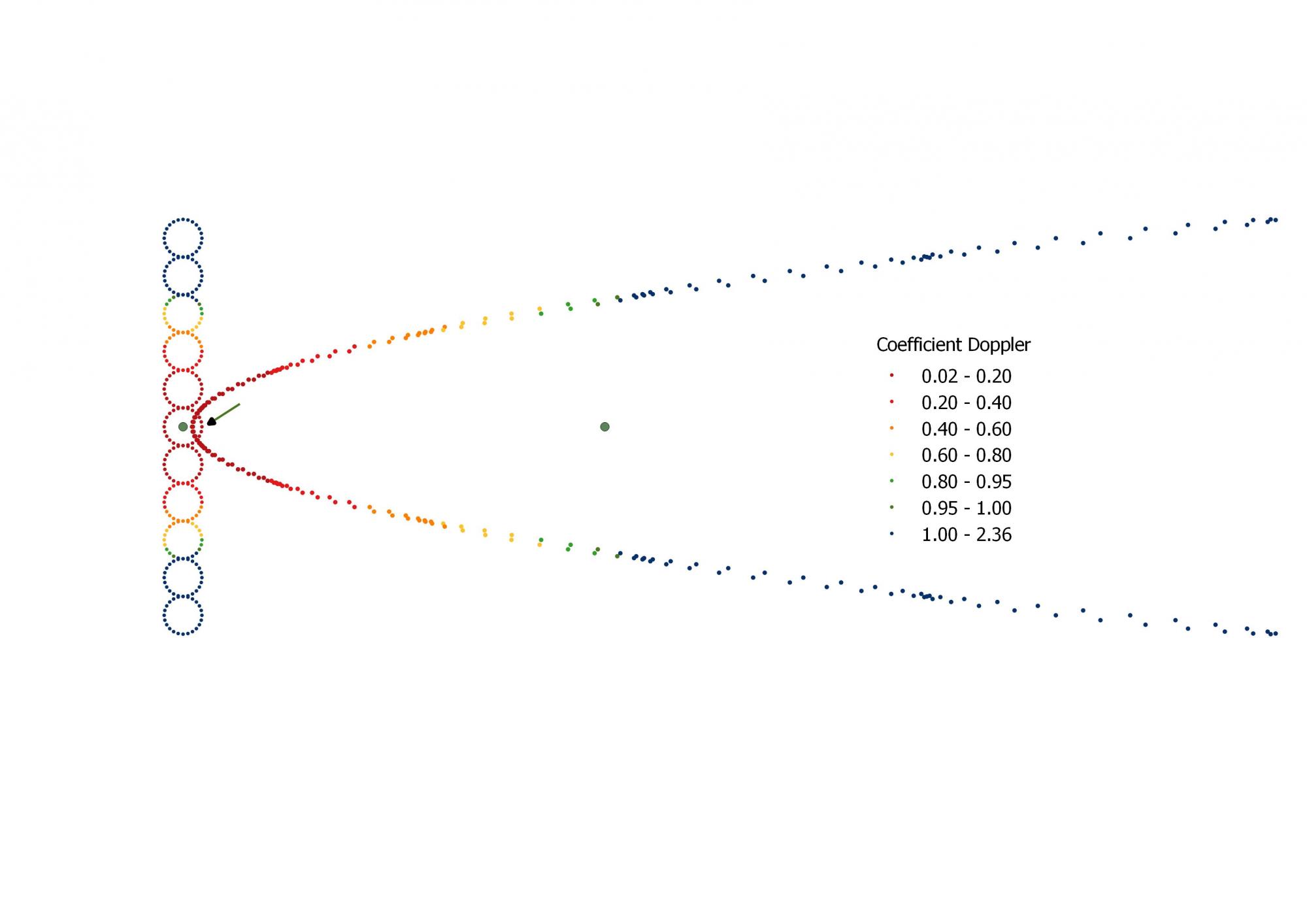
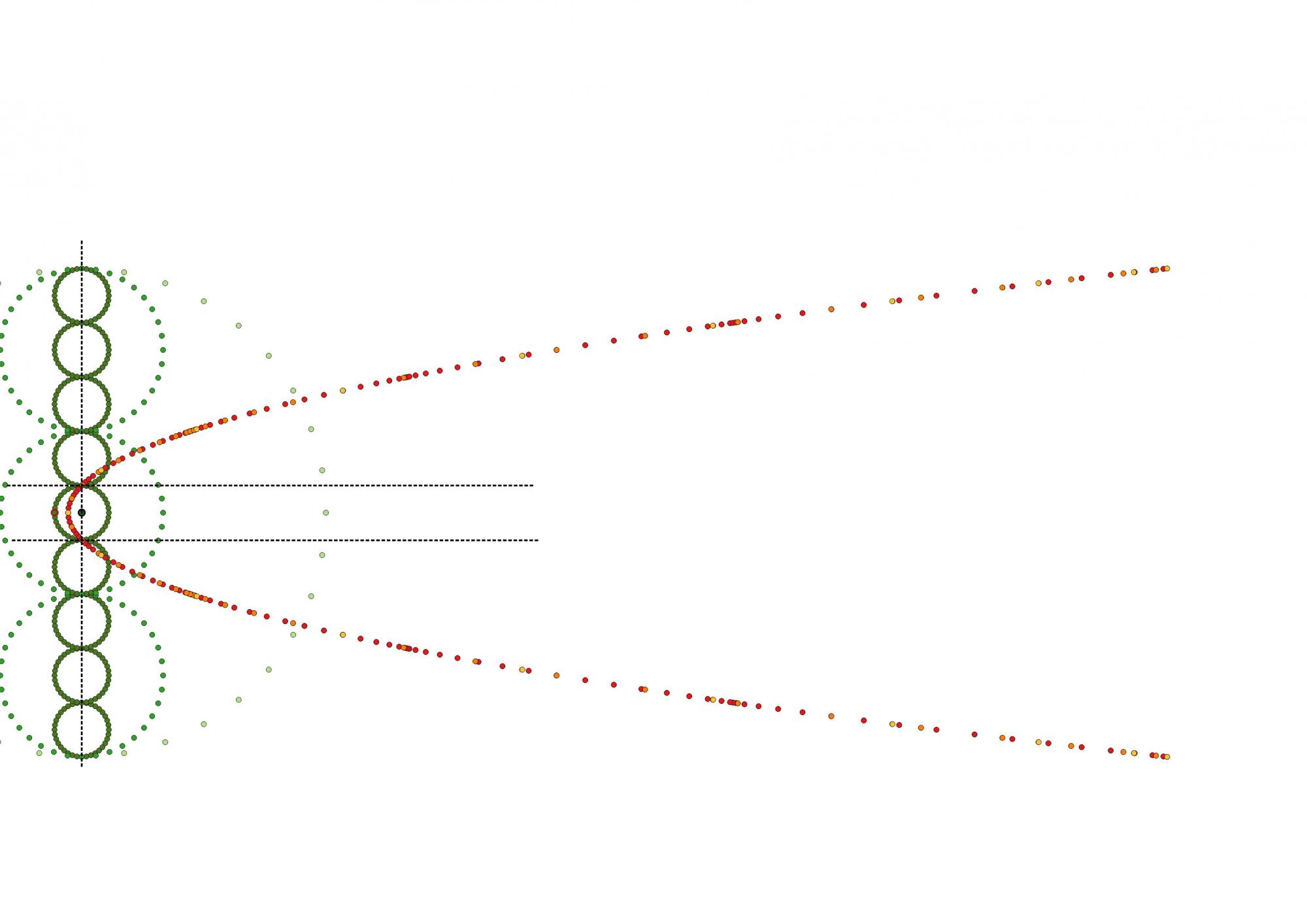
D'accord, ca explique le haricot... l'observateur n'est plus au centre du cercle, ta figure est trompeuse. En fait j'ai l'impression que ta "parabole" (ou presque, car la parabole parfaite doit etre pour v=c) est la forme physique de l'horizon visuel futur, dont on parle dans les posts précédents, que l'observateur se trimbale quelle que soit sa positionJ'essayerai de faire un petit dessin quand je pourrai pour clarifier (et verifier..) ce discours.
A +
Trollus vulgaris
Bonjour,
J'ai hâte de connaitre le résultat.
J'aimerai bien quand tu auras le temps que tu fasses pour le référentiel des accélérés la même chose que le 136.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
Alors maintenant tu nous colle des graphs sans un texte ni calcul et on doit tout deviner... arg, je passe sur celui là.
Je l'ai gribouillé à la main donc j'ai une petite idée, mais je vous epargne le brouillon.
Et y'a toujours des surprises au passage à l'échelle...
C'est plus ou moins au programme, si c'est pas trop compliqué... (J'ai l'espoir que ce soit tres simple en fait, à voir). J'ai commencé les coordonnées de Rindler "redressé" abordées en debut de fil dont ceci serait la suite logique, mais je prend du retard a cause des parentheses de parentheses... et ni vu ni connu y'a les coordonnées Lass qui sont venues se glisser (NB : Je ne vous suis pas en section physique).J'aimerai bien quand tu auras le temps que tu fasses pour le référentiel des accélérés la même chose que le 136.
Donc on est pas encore de retour au sujet initial du fil (peut etre hors de portee) car perso ce que je cherche au fond c'est transposer la representation du message 136 au trou noir : que voit un stationnaire et que voit un chuteur, pas gagné... d'autant que j'ai un poil qui pousse au milieu de ma paume
A bientôt
Mailou
Trollus vulgaris
Salut Mailou,
le graph c'est celui de ce message
http://forums.futura-sciences.com/as...ml#post6002052
C'est celui des accélérés
Pourquoi ne vas tu pas en section physique?
Après la transposition Rindler à la gravitation, ça m'intéresse aussi mais il faudrait partir de la bonne hypothèse de départ, peut être avec les coordonnées KS qui sont également dans le lien wiki ??
Pour j'ai hâte de voir le résultat, c'est par rapport au message 141.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Alors voilà ce que j'obtiens...
Trois déformations d'une même figure plane composée de cinq petits cercles et deux grands.
Le voyageur accélère à a=0.05c/s ce qui place l'intersection entre son horizon de Rindler (droite jaune) et son espace à 20sl derrière lui (=1/0.05).
Les trois positions de l'observateur sont en Bleu clair, Bleu foncé et Violet. Son temps propre et sa vitesse instantanée sont notés pour chaque figure.
Rouge, Orange, Bleu clair et Bleu foncé sont à peu près les mêmes que dans le dessin du message 136 et on peut vérifier qu'ils se comportent de la même façon. Les positions de l'observateur en Noir, Bleu clair et Bleu foncé sont donc équivalentes à celles du message 136 mais j'avais triché sur les distances pour que les temps propres tombent justes, ce n'est pas le cas ici. On voit que Rouge se rapproche de la coordonnée vue -10sl, qu'Orange s'en éloigne dans un premier temps pour y revenir et que Bleu foncé, après s'être éloigné vers l'avant va revenir traverser l'observateur et s'entasser avec ses petits copains entre l'observateur et la coordonnée -10sl.
On retrouve donc parmi les déformations des formes similaires aux dessins que tu proposes aux messages 123,137 et 139. J'ai mis en valeur la traversée du petit cercle plus foncé et on voit bien les formes goutte > ellipse > haricot se succéder sauf qu'on a en plus le paramètre d'accélération car la vitesse et donc la déformation augmente. On peut le voir en comparant le haricot "sortie du petit cercle foncé" en Violet et le haricot "sortie du petit cercle central" en Bleu clair.
Mais je n'ai pas fait tout ça pour le plaisir de jouer avec l'aberration, ce qui m'intriguait c'était cette histoire de coordonnée -10sl qui suit l'observateur et vers laquelle tous les objets traversés vont tendre. De la même façon, tous ceux qui se situaient derrière vont s'avancer visuellement pour atteindre cette coordonnée. La construction qui est donnée ici lie donc la vitesse variable (accélération dans le Minko), la position variable par rapport l'objet observé (cercles) et la déformation vue (aberration) et montre comment l'observateur va se trimballer derrière lui une courbe "fictive" (pointillé jaune) sur laquelle tous les objets viennent s'écraser, tôt ou tard... on obtient alors la parabole que tu donnes au message 130 (0.99999...c).
En haut à droite j'ai tracé cette parabole dont l'intersection avec la direction du déplacement se situe à -10sl (-1/2a), visuellement, sur laquelle tous les objets sont alors confondus. L'horizon de Rindler définit les valeurs de temps propres alors vues pour les objets notés par couleur. Par exemple on sait que Rouge ne pourra être vu plus vieux que T=0, à moins d'atteindre réellement c et l'infini, the end, comme représenté, humm... Etrangement ça veut dire que tout au long de son voyage vers l'infini l'observateur pourra toujours faire la part des objets qui étaient derrière lui à -10sl (dimension exacte dans l'espace) au départ, de ceux qui étaient devant (à part en limite quelques "border" qui trahissent la règle, genre Orange).
Je n'ai pas encore tout bien digéré mais bravo pour cette découverte ! Pour moi l'horizon de Rindler était la droite à 45° du Minko, rayon lumineux que l'accéléré ne pourra jamais voir, mais alors c'est quoi cette parabole ?? l'horizon de Zef ?
A +
Mailou
Trollus vulgaris
Bonjour Mailou,
Si cette parabole est véritablement une découverte venant de moi ( voire d'Alain Bernard https://www.youtube.com/watch?v=DATADtftNpk)
Ce n'est pas à moi de savoir si on doit nommer cet horizon horizon de ZEF-A.BERNARD.
je proposerais plutôt Horizon visuel de Rindler ou horizon futur de Rindler ou même plus simplement Horizon de Rindler puisqu'il n'a de sens que pour l'Accéléré de Rindler.
merci pour l'honneur en tous cas et merci pour les schémas.
Zefram.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
De rien, merci pour la leçon !merci pour l'honneur en tous cas et merci pour les schémas.
.....
J'ai regardé ce que ça donne en 2D+t pour essayer de déterminer les âges auxquels sont vus les objets déformés. J'ai représenté l'observateur à la position Bleu foncé du dernier schéma (T=26.3s et B=0.86 pour a=0.05c/s). Pour savoir ce qu'il voit il faut se mettre dans son repère, sa trajectoire jusqu'à ce point est représentée en vert clair + pointillés pour le futur s'il continue d'accélérer. Tous les points colorés sont alignés à T=0 sur la droite noire puis filent à 0.86c du voyageur, à ce moment là.
A l'intersection entre l'horizon de Rindler et les trajectoires des objets colorés on peut y lire leur temps propre "maxi" correspondant aux chiffres de la dernière figure. Et à l'intersection entre le cône passé et les trajectoires on lit l'âge "vu" à ce moment là (très approximativement des multiples de 5, on voit que les points sont loin du cône mais c'est pour la compréhension..) : de Rose -15 à Bleu clair 25 derrière, Violet 25 et Gris -5 devant.
On voit donc que Bleu clair et Violet sont vus tous les deux à ~25s et l'analyse (il faudra me faire confiance là dessus, j'ai vérifié) montre que tous les points situés sur l'ellipse sont vus à ce même âge. Par extension on voit que les cercles colorés (projection du voyageur dans son plan de départ) déformés en ellipses indiquent aussi des temps propres égaux, notés ~-5 à 25 + 35 en Bleu foncé. C'est donc un mode de lecture assez simple : intersection entre objet déformé et ellipse datée = âge vu. Mais en fait il y a encore plus simple, pas si évident dans ce contexte mais logique puisque le voyageur reçoit le même photon (..?) que l'inertiel, Bleu foncé, soit par exemple 35-30=5s pour Orange puisqu'il se trouve dans son espace (distance propre) à 30sl de Bleu foncé.
Enfin, on imagine que si le voyageur continue d'accélérer, chaque changement de repère suivant va rapprocher la droite noire ("espace" T=0) de celle juste en dessous en pointillé à 45°. Les objets, dépassés au fur et à mesure, s'entasseront en inclinant leur trajectoire et se confondant eux aussi avec le pointillé noir. A ce moment là le voyageur a atteint c à l'infini, comme dans le dernier dessin.. et le plan de départ (celui des cercles et de tout ce qui se trouvait devant et derrière à l'infini) se trouve visuellement "réduit" en 1D sur cette hyperbole.
On comprend aussi que le point de rotation de la droite noire (T=0), par changement de repère, se trouve immuablement en Rouge à T=0, à 20sl (1/a) derrière le point de départ (devenu vert dans ce dessin) comme expliqué pour le Minko du dernier dessin. Et donc, que la parabole sera l'intersection entre le cône passé l'espace 2D-temps de départ devenu plan !..?
J'espère que le dessin reste lisible j'ai fait au mieux
Mailou
Dernière modification par Mailou75 ; 18/11/2017 à 02h12.
Trollus vulgaris
Just for fun
Trollus vulgaris
Salut,
Tu as raison, cela a carrément de la gueule en 3D et on fait bien le lien avec les schémas du 145 .
Ta présentation ne correspond pas à la mienne mais elle en demeure pas moins valide.
Pour comprendre le 147 , il faut lire avant le 145 et le 148 et comprendre que l'accéléré passe du noir au cyan puis au bleu et au violet.
cela dit, il ne doit pas y avoir bezef comme références non plus...
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut et merci
Les images ne prouvent rien seules. Données telles quelles au debut elles n'auraient eu aucune legitimité. Elles sont l'aboutissement et la simplification de "ton" problème. Elles permettent toutefois a celui qui n'a rien compris au debut de la page de pouvoir la lire a l'envers : L'aberration n'est que l'intersection entre un cone passé et des objets en mouvement (ligne d'univers diagonale) compressés de gamma dans l'espace euclidien de l'observateur. Le petit objet au dessus restitue la dimension manquante. Accessoirement ça permet aussi à ceux qui croient avoir compris (je nous compte au moins tous les deux dans le lot) de verifier qu'on a pas dit trop de c...
.......
Sur un autre sujet et pour ne pas devier le fil "Rindler", l'espoir que j'avais de pouvoir decrire ce que voient les observateurs stationnaires de KS en transposant la logique de ce que voient les accélérés de Rindler s'evanouit... parce que le plan euclidien instantané de Rindler est graduable en "mètre", alors que celui de KS ne l'est pas, donc c'est pas encore gagné ! Sniiiff
Trollus vulgaris
