calcul trajectoire d'un photon - Trou noir.

[Zefram Cochrane]

Bonsoir,
J'ouvre ce sujet suite à la demande de Mailou.
Je voudrais avoir l'équation de la trajectoire d'un photon dans le champ de gravitation d'un TN de rayon Rs, partant initialement suivant d'une distance Ro suivant l'axe X
J'ai comme formule (cf Relativité générale Moore chapitre 12 page 144)
l'équation 12.1

avect la coordonnée temporelle de Schwarzschild.
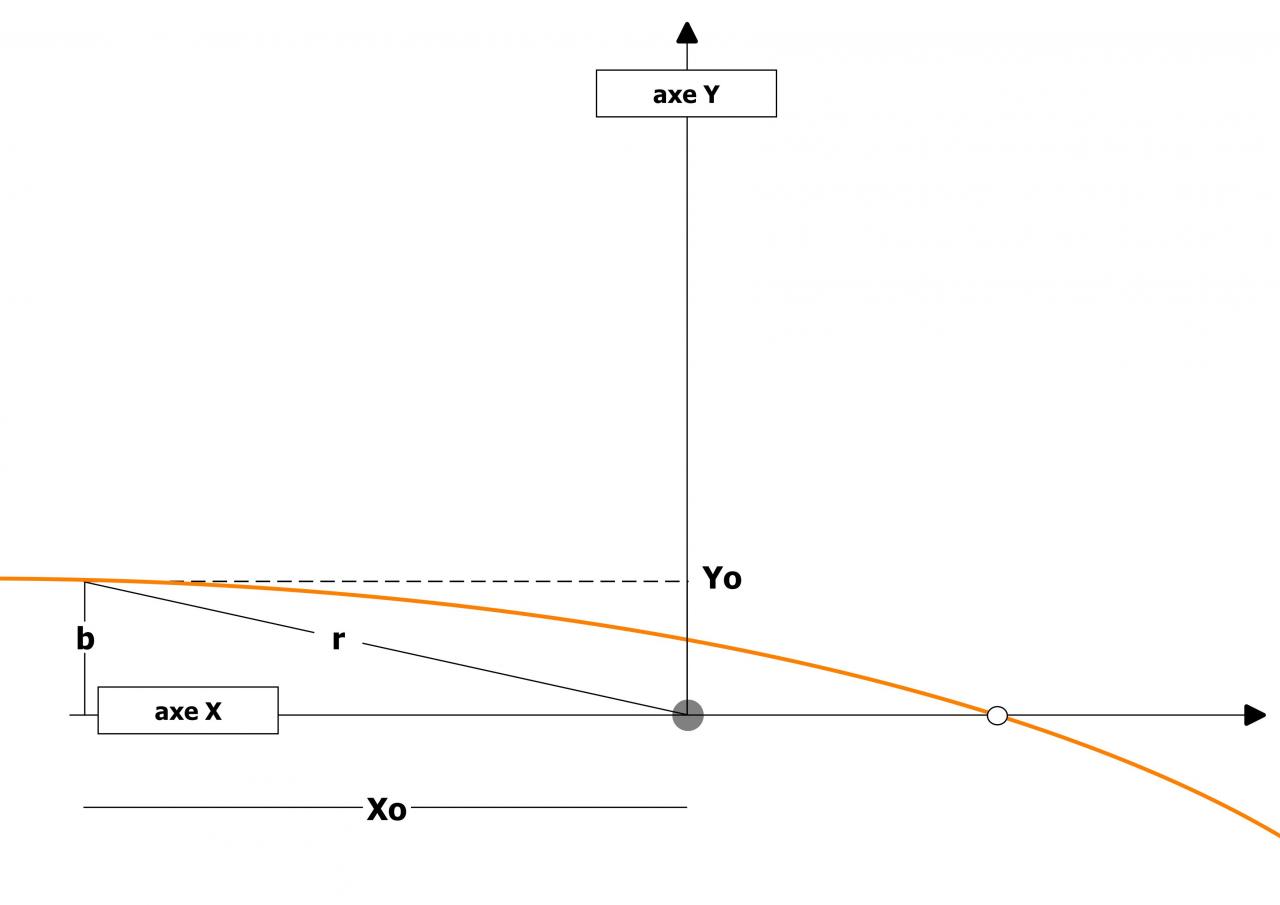
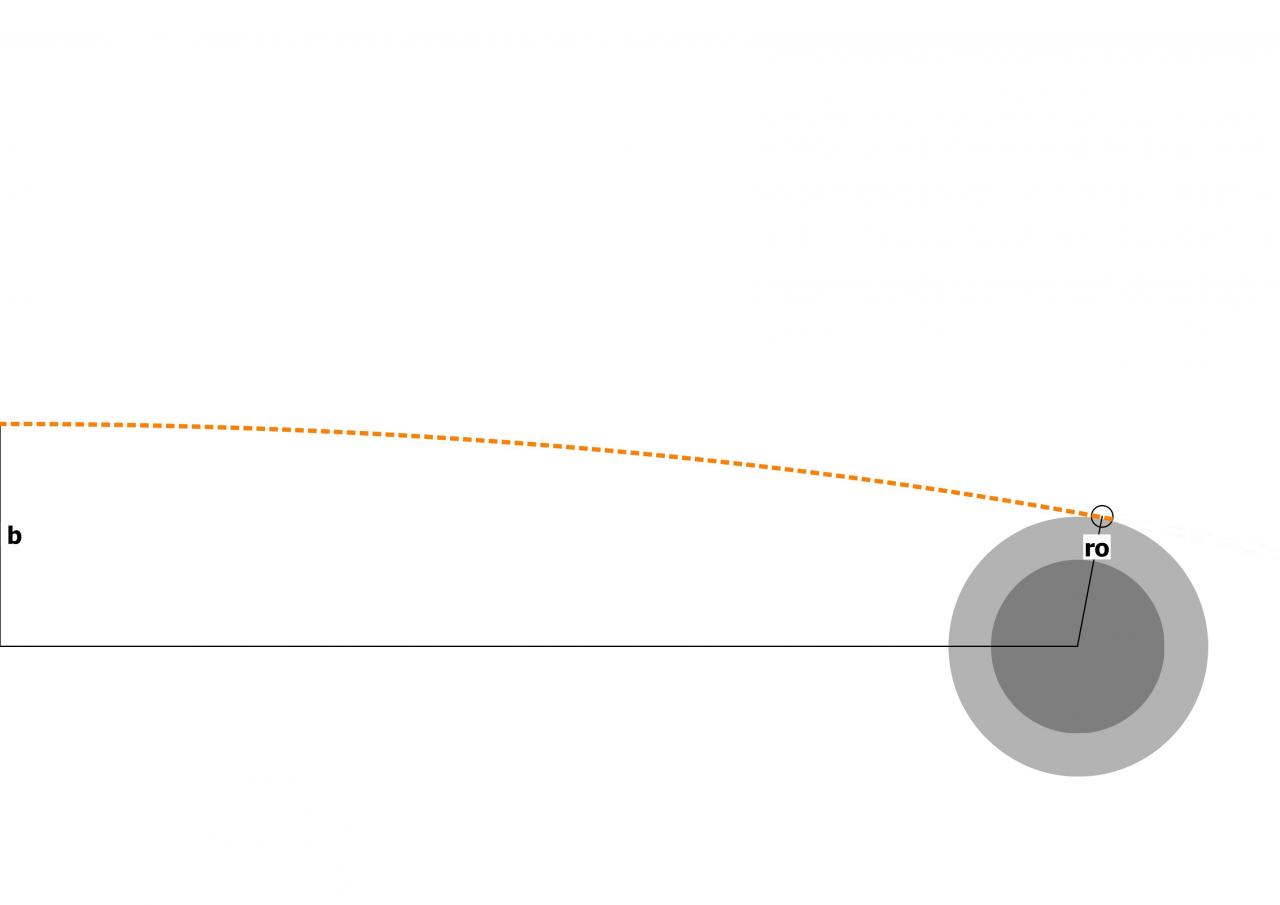
J'ai le schéma suivant :



Sur ce schéma , et et b étant le paramètre d'impact.
Mon objectif estde trouver la coordonnée X de l'observateur stationnaire par rapport au TN et qui percevra le photon.

J'aurais besoin de connaitre les coordonnées X et Y en fonction de phi.
Merci de votre aide.

P.S
dans la discussion de Mailou, Jacknicklaus donne une formule qu'il décrit comme étant le diamètre apparent du TN du point de vue d'un chuteur chutant depuis l'oo.

https://forums.futura-sciences.com/d...ml#post6606853

Je ne doute pas de la formule mais vu la description, il semblerait que ce soit la vision d'un Stationnaire à r du TN ( alain.R m'avait donné comme valeur pour un chuteur venant de l'oo un demi angle apparent de 83° au niveau de Rs et non pas 180
P.S je n'arrive pas à visualiser les formules sur mon ordi, j'espère que vous arriverez à la lire.
-----

[jacknicklaus]

Bonjour à tous.

compliqué.
On peut obtenir une équation différentielle séparée en t et r, mais qui n'a pas de solution analytique exacte.
On peut obtenir une forme t = f(r) en restant à grande distance (r >> GM). C'est l'effet Shapiro.


nota : unités RG, c = 1.

On part de ds² = 0 pour une ligne d'univers de photon :


on utilise le paramètre d'impact b (quantité conservée) et r0 la coordonnée radiale de moindre approche du signal par rapport au TN de masse M



on obtient :

qui n'a pas de solution analytique, afaik.

Mais si on considère GM/r << 1, on peut faire un DL au premier ordre en GM/r qui donne :
où N(r) est le terme Newtonien, et A(r) et B(r) les correctifs RG, tous positifs :
dont une primitive est
dont une primitive est
dont une primitive est
finalement (t=0, r = r0)

C'est l'effet Shapiro.

[jacknicklaus]

dans la discussion de Mailou, Jacknicklaus donne une formule qu'il décrit comme étant le diamètre apparent du TN du point de vue d'un chuteur chutant depuis l'oo.

https://forums.futura-sciences.com/d...ml#post6606853

Je ne doute pas de la formule mais vu la description, il semblerait que ce soit la vision d'un Stationnaire à r du TN.

Non, il s'agit bien de ce que voit un observateur en chute libre radiale. Le cas des stationnaires donne des résultats différents, en effet.

Puisque tu as le Moore, ces 2 cas sont traités dans les problèmes de fin de chapitre si je me souviens bien.

[Zefram Cochrane]

Bonjour,
Je te remercie de ta réponse développée.

on utilise le paramètre d'impact b (quantité conservée) et r0 la coordonnée radiale de moindre approche du signal par rapport au TN de masse M

Je trouve cette formule très intéressante parce qu'elle dit qu'un observateur à l'oo qui se trouve décalé à par rapport à une radiale du TN et émettant un faisceau laser parallèlement à la radiale sera perçu tangentiellement par un observateur stationnaire situé à la coordonnée radiale de moindre approche ro= 3GM ( dernière orbite des photons) du TN et il se verra à une altitude apparente ho = b du TN.
Ma quiestion est ou se trouvera le Stationnaire angulairement parlant. L'angle entre b (vertical) et la radiale oblique du Stationnaire.
( comme le Stationnaire perçoit les photons tangentiellement, ceux ci se mettent en orbite autour du TN si on devait prolonger leur trajectoire)
Cordialement,
Zefram

[A voir en vidéo sur Futura]

[Mailou75]

Salut,

Je suis allé regarder un peu le problème et, avec les maigres moyens dont je dispose, je trouve que :

(Pour la notation ~2,6.Rs et en supposant que le rayon lumineux dont tu parles est le même que celui qui donne l'angle limite quand on est proche du TN dans les calculs de Jacknicklaus)

1 - Celui à l’infini voit un TN de diamètre apparent ~2,6.Rs
Comme il est à l’infini l'angle sur le champ visuel est ~0
Le voyageur en chute libre voit la même chose puisque sa vitesse est alors nulle

2 - Un immobile à ~2,6.Rs se trouve dans son repère à ~3,3.Rs en mètres locaux du centre du TN
Il voit les rayons lumineux en question avec un demi-angle de ~56,5°
Le voyageur en chute libre à ~2,6.Rs se trouve dans son repère à ~2,6.Rs en mètres locaux du centre du TN
(cas particulier pour les chutes depuis l'infini, le chuteur et l'observateur éloigné partagent le même espace euclidien)
Il a une vitesse locale B~0,62 et voit un cône réduit de ~29,1° du fait de l'aberration

3 - Un immobile à ~1,5.Rs se trouve dans son repère à ~2,6.Rs en mètres locaux du centre du TN
Il voit les rayons lumineux en question avec un demi-angle de 90° (ceux qui tournent en rond)
Le voyageur en chute libre à ~1,5.Rs se trouve dans son repère à ~1,5.Rs en mètres locaux du centre du TN
Il a une vitesse locale B~0,81 et voit un cône réduit de ~35,2° du fait de l'aberration

Je trouve cette formule très intéressante parce qu'elle dit qu'un observateur à l'oo qui se trouve décalé à par rapport à une radiale du TN et émettant un faisceau laser parallèlement à la radiale sera perçu tangentiellement par un observateur stationnaire situé à la coordonnée radiale de moindre approche ro= 3GM ( dernière orbite des photons) du TN

Du coup selon moi ceci est juste (voir 1)

et il se verra à une altitude apparente ho = b du TN.

et cela aussi (voir 3)

.....

Par contre il y aurait un méli melo dans les valeurs données par Jacknicklaus qu'il faudrait interpréter comme : "Un immobile qui se trouve à 1,5.Rs mais dont la position dans son repère le place à ~2,6.Rs du centre reçoit les photons en orbite selon un demi-angle de 90°". Donc ce ne serait pas le chuteur qui voit cet angle mais bien l'immobile comme tu le suggérais et la coordonnée de Schwarzschild n'est pas r~2,6.Rs mais bien r=1,5.Rs.

.....

qui n'a pas de solution analytique, afaik.

Je ne sais pas si cette formule est la fameuse "qui n'a pas de solution analytique" mais perso ça ne me dérange pas de tatonner si je sais comment l'utiliser. L'ennui c'est que je vois pas d'angle (ni départ, ni arrivée, ni paramètre pour repérage cylindrique) donc je ne comprends pas comment elle pourrait être "générale" ? Avoir ça ne permet pas de déterminer ce qui est vu car il y a d'autres sujets mais ça peut déjà donner les angles de visée (voir mon récent fil sans réponse...).

A+

[jacknicklaus]

L'ennui c'est que je vois pas d'angle (ni départ, ni arrivée, ni paramètre pour repérage cylindrique) donc je ne comprends pas comment elle pourrait être "générale" ?

Bonjour,

faut l'utiliser couplée avec la relation entre b (qui est une constante) et dPhi/dt.

.

On a donc le système dPhi/dt = *** et dr/dt = ***

ca nous donnerait avec une solveur numérique du PHi = f(t) et du r = g(t) où t est le paramètre de la courbe.

[Zefram Cochrane]

Bonjour,
J'ai la formule du demi-angle critique du rayon apparent du TN pour un Stationnaire ( donné par le Moore) situé à la coordonnée r :
12.14
On reconnait la distance apparente séparant le Stationnaire du centre du TN.
Il est intéressant de noter que cette formule fait apparaitre un sinus et non une tangente ???

le demi-angle critique passe de 0 à 90° pour r allant de GM à 3GM et de 90° à 0 pour r allant de 3GM à +oo


Une réponse à cette question pourrait aider : peut-on calculer la trajectoire d'un photon tiré perpendiculairement à la radiale du TN par le Stationnaire pour r donné?
merci de vos réponses,
Zefram
Je n'ai malheureusement pas de solveur non plus.
Après je peux avoir me semble-t'il une solution approximative pour r>> 3GM

[Mailou75]

le demi-angle critique passe de 0 à 90° pour r allant de GM à 3GM et de 90° à 0 pour r allant de 3GM à +oo

Comme c’est un sinus tu dois pouvoir remplacer le zero rouge par 180

Ce qui veut dire qu’à r=2,6Rs (le rac(27).GM) l’angle pour un immobile est inférieur à 90°. L’aberration pour celui qui chute aurait tendance à diminuer cet angle donc comment Jacknicklaus obtient-il un élargissement de l’angle à 90° pour cette valeur de r ?

......

@Jacknicklaus

J’ai regardé un peu les formules, je te réponds demain, merci

[Zefram Cochrane]

Bonjour à tous.

compliqué.
On peut obtenir une équation différentielle séparée en t et r, mais qui n'a pas de solution analytique exacte.
On peut obtenir une forme t = f(r) en restant à grande distance (r >> GM). C'est l'effet Shapiro.


nota : unités RG, c = 1.

On part de ds² = 0 pour une ligne d'univers de photon :


on utilise le paramètre d'impact b (quantité conservée) et r0 la coordonnée radiale de moindre approche du signal par rapport au TN de masse M



on obtient :

qui n'a pas de solution analytique, afaik.

Mais si on considère GM/r << 1, on peut faire un DL au premier ordre en GM/r qui donne :
où N(r) est le terme Newtonien, et A(r) et B(r) les correctifs RG, tous positifs :
dont une primitive est
dont une primitive est
dont une primitive est
finalement (t=0, r = r0)

C'est l'effet Shapiro.

Bonjour,
J'avais déjà vu ce genre de calcul dans le message suivant :
https://forums.futura-sciences.com/a...ml#post3760320
on obtient le dernier résultat , c'est-à-dire l'effet Shapiro ( distance radar) sur la radiale en calculant l'intégrale de la vitesse coordonnée de la lumière :

Je pense que cela peut-être généralisable pour un photon tiré avec un angle par rapport à la radiale entrante depuis ro.
Si vous avez des idées.
Merci pour votre aide
Zefram

[Zefram Cochrane]

Bonjour,
on sait calculer facilement l'altitude apparente d'un stationnaire à la coordonnée r :

Ce que je cherche, c'est avoir la formule pour obtenir la coordonnée r en f° de R'.
quelqu'un saurait?

[yves95210]

Une petite transformation donne l'équation du troisième degré :


Et quand (comme moi) on ne sait pas ou plus faire, suffit de faire appel à son moteur de recherche préféré, et on tombe sur la méthode de Cardan, et il n'y a plus qu'à appliquer les formules.

[Zefram Cochrane]

Merci Yves,
j'étudierai en détail la méthode de Cardan.
Est-ce un hasard selon toi si 27 qui est dans la méthode correspond au carré du paramètre d'impact minimal d'un photon qui atteindra la dernière orbite des photon tangentiellement?

[yves95210]

Merci Yves,
j'étudierai en détail la méthode de Cardan.
Est-ce un hasard selon toi si 27 qui est dans la méthode correspond au carré du paramètre d'impact minimal d'un photon qui atteindra la dernière orbite des photon tangentiellement?

Il manquait un carré dans l'équation dans mon message précédent. C'est en fait r³-R'²r+2GMR'²=0

Avec les notations de l'article en lien, p=-R'² et q=2GMR'² , donc Δ = 4R'⁶-27(2GMR'²)² = 4R'⁴(R'²-27(GM)²).

Δ s'annule lorsque R'=racine(27)GM, et la solution change de forme suivant que Δ est < ou > 0. Ce n'est donc pas étonnant qu'il y ait un lien avec une limite physique. Mais je n'ai pas été voir plus loin.

[Zefram Cochrane]

Bonjour,
Je ne comprends pas:
Cela fait plusieurs fois que j'essaye d'appliquer la méthode de Cardan mais je n'arrive pas à retomber sur mes pattes ????
Je suis d'accord sur le Delta mais après cela ne me donne pas de résultat cohérent lorsque je vérifie???

[yves95210]

Salut,

Je n'ai pas regardé ton problème dans le détail, mais je suppose que tu t'intéresse au cas Δ>0, c'est-à-dire R'²>27(GM)².

Dans ce cas, as-tu vu que la page suivante du wiki redonne les trois racines réelles de l'équation sous une forme qui te conviendra peut-être mieux (à la fin de la section "Présentation trigonométrique des racines d'une équation ayant trois racines réelles") ?

Sauf erreur de ma part (j'ai simplifié de tête pour ne pas avoir à écrire trop de lignes de TeX, mais je te conseille de vérifier), la première solution est


et les deux autres s'en déduisent en ajoutant à l'arccosinus.

A vue de nez c'est cohérent : comme on a , on est bien dans le domaine de définition de la fonction arccos.

[Zefram Cochrane]

Bonjour,
Merci Yves pour la solution elle fonctionne impecable
La formule que tu m'a donné donne bien R en f° de R' pour R> 3GM
la seconde +2pi me donne un résultat négatif qui n'a probablement pas de sens physique (????)
la troisième -2pi me donne R en f° de R' pour R< 3GM
correspond à l'altitude minimale à laquelle un stationnaire se voit du centre du TN
merci encore.
Zefram

[Mailou75]

Salut,

On savait calculer facilement ce que tu appelles R’ (cad la distance en mètres locaux par rapport au centre du TN pour le repère «type Schwarzschild» d’un observateur qui n’est pas à l’infini, accessoirement c’est ce qui est vu) en fonction de r. Maintenant on sait calculer r en fonction de R’, on est pas tellement plus avancé... on est loin des trajectoires 2D (voire 2D+t) pour des géodésiques nulles.

Il serait plus interessant de réviser/corriger les formules de Jacknicklaus (qui pour ce que j’en ai vu ne marchent pas bien) et obtenir une réponse pour le sujet du fil. Je sais que c’est les vacances mais là vous faites des calculs qui ne servent à rien...

A +

[Zefram Cochrane]

Bonjour,
Je ne suit pas en mesure de calculer la trajectoire de la lumière arrivant à un observateur se trouvant à une position P par rapport à un TN connaissant la position S de la source.
Par contre je suis en mesure de calculer connaissant la position S' de la source, je peux être en capacité de calculer la position P de l'observateur s'il veut voir la source sous un certain angle.

Sur ce schéma:
les faisceaux lumineux sont émis horizontalement depuis l'oo avec un paramètre d'impact b tel que la coordonnée radiale de moindre approche soit 3GM 6GM et 9GM.
la tangente en un point de la trajectoire avec l'horizontale forme un angle avec l'horizontale donné par cette formule ou phi_c est la moitié de l'angle du diamètre apparent du TN vu par l'observateur stationnaire.
il est de 30° pour R=3GM.

[Mailou75]

Salut,

Réponse pour le moins étrange ...

Je ne suit pas en mesure de calculer la trajectoire de la lumière arrivant à un observateur se trouvant à une position P par rapport à un TN connaissant la position S de la source.
Par contre je suis en mesure de calculer connaissant la position S' de la source (...)

Je ne vois pas bien la différence que tu fais entre un faisceau entrant ou sortant, en 2D la trajectoire reste la même dans un sens ou l'autre.

les faisceaux lumineux sont émis horizontalement depuis l'oo avec un paramètre d'impact b tel que la coordonnée radiale de moindre approche soit 3GM 6GM et 9GM.

Humm... la coordonnée de moindre approche est un genre de "périastre" donc a priori un point de symétrie pour la trajectoire 2D. De plus, si tu as utilisé les formules de jacknicklaus je pense que tes courbes sont fausses car, à la coordonnée de moindre approche, la trajectoire est orthoradiale (perpendiculaire à la radiale). Assez logique si on veut que ce soit un point de symétrie. Donc pas d'accord avec tes courbes, et de toute façon pas d'accord avec la formule de jacknicklaus qui déconne (voir analyse ici : https://forums.futura-sciences.com/d...ml#post6612403)

.....

Ca n'enlève rien au fait que les calculs précédents (messages 10 à 16) sont sans intérêt.

[Zefram Cochrane]

J'écris depuis un portable. Donc réponse plus complète dans une semaine.
Il faut faire une rotation de phi-c / R pour avoir un point orrhoradial au niveau du périgée.
Je ne avais pas fait sur le schéma précédent pour montrer les résultats bruts issus du calcul
Il faut comprendre que sur ce schema, localement, chaque stationnaire se voit a une hauteur b par rapport a la radiale parallèle a la trajectoire apparente du photon.

[Mailou75]

Il faut faire une rotation de phi-c / R pour avoir un point orthoradial au niveau du périgée.

Ça a une unité ce truc là ?

Il faut comprendre que sur ce schema, localement, chaque stationnaire se voit a une hauteur b par rapport a la radiale parallèle a la trajectoire apparente du photon.

On est à la limite du pipotron tu nous la refais ?

(perso je trouvais le schéma du message 4 plus fidèle à ce que donnent les formules de Jacknicklaus, départ orthoradial en Ro, et limite de validité à 1,5Rs)

[JPL]

Petit rappel du sous-titre de ce forum :

Ce forum est réservé à des discussions théoriques ou techniques entre professionnels, semi-professionnels ou étudiants de niveau master.

[Mailou75]

Effectivement, la question ne s’adresse pas à n’importe qui. Comme certains maitrisent la TQC on a l’espoir d’avoir des réponses en relativité...