Bonsoir,
J'aimerais vous soumettre une question d'ordre général mais qui fait appel à une bonne maitrise du sujet, c'est pourquoi je poste volontairement la question dans la section "pros". Je reprends actuellement une étude, que j'avais laissée en standby, sur ce que voit un observateur en chute libre vers un trou noir et je bute toujours sur la même chose.
Le sujet s'inscrit dans le cadre : Trou noir de Schwarzschild + déplacement radial + chute depuis l'infini + uniquement au dessus de l'horizon. J'arrive très bien à déterminer comment l'observateur éloigné voit l'environnement du trou noir et le voyageur en chute libre. J'arrive aussi à déterminer ce que voit un observateur à r donné, son environnement et le voyageur, quelle que soit sa position par rapport à r. Mais je n'arrive pas à établir avec certitude ce que voit celui qui chute, même en se restreignant au cas radial. La difficulté ici va être d'arriver à faire comprendre ma question...
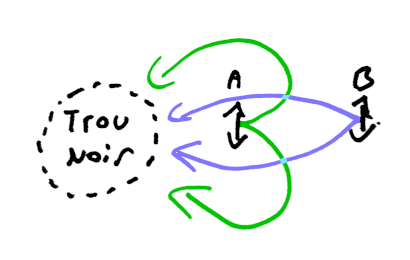
Le principe d'aberration de la lumière en relativité restreinte nous dit : Si un observateur A voit un objet à une distance de 1km et qu'un objet B passe à coté de A à 80% de la vitesse lumière, alors au même instant (évènement de croisement), B verra le même objet à 3km, car le Doppler radial vaut z+1=3 pour v=0,8c. Jusqu'ici pas de problème...
Prenons maintenant un observateur A en r qui voit l'horizon du trou noir à une distance de 1km et supposons qu'au passage à cette coordonnée r, notre voyageur B à justement une vitesse locale de chute libre de 0,8c (les valeurs réelles n'ont aucune importance dans le cadre de la question). En supposant que pour A tout est "visiblement plat" (il ne voit pas les déformations de l'espace-temps, au mieux il voit des shifts) et en appliquant le principe d'aberration précédemment cité on trouve que le voyageur voit l'horizon du trou noir à 3km !
Le premier point est de savoir si le principe est applicable... mais il est évident que A et B reçoivent les mêmes photons et donc les mêmes informations de leur environnement, avec lesquelles ils vont fabriquer des images différentes. Ce que voit B est donc une déformation de ce que voit A, qui plus est, localement (RR) en accord avec le principe d’aberration.
J'ai tenté par d'autres moyens, pour justifier de ce résultat, de dessiner "le repère de celui qui chute" et j'obtiens presque la même chose que ce qui est décrit plus haut. Ceci m'amène à trois questions :
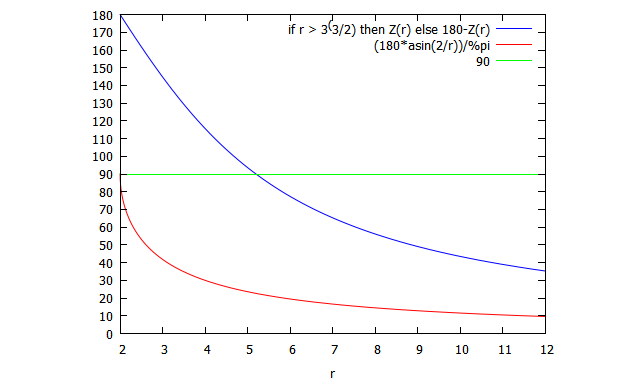
1/ Si le principe décrit est juste de façon générale (on pourra discuter des détails plus tard) alors ça veut dire que plus r est est petit, cad que A est proche de l'horizon du trou noir, plus la vitesse de chute de B sera grande et tendra vers c et donc que : plus B s'approche de l'horizon (vu par les immobiles), plus il va voir l'horizon s'éloigner car le Doppler radial/aberration (le z+1 associé à sa vitesse) va tendre vers l'infini à mesure que la vitesse locale tend vers c.
2/ Dans le système que j'ai essayé d'établir que trouve "presque" la même chose, mais pas tout à fait... Serait-il possible que B ne prenne pas simplement l'image vue par A et la transforme via l'aberration, stricto RR, mais que ce que voit B soit quelque chose de "proche" mais pas exactement l'application de l'aberration en espace plat ?
3/ Pourquoi le système de coordonnées de Lemaître, réputé celui de l'observateur en chute libre depuis l'infini n'est-il pas celui qu'on cherche ? On ne peut pas projeter le cône passé sur un plan euclidien perpendiculaire à la ligne de vie (axe temps du repère) pour produire ce que voit le voyageur. Quelles sont les caractéristiques du repère recherché, puisque le mien n'est peut être pas le bon non plus ..?
Merci pour votre attention et merci d'avance pour vos réponses
Mailou
-----