Trou noir et chute libre : application numérique

[Zefram Cochrane]

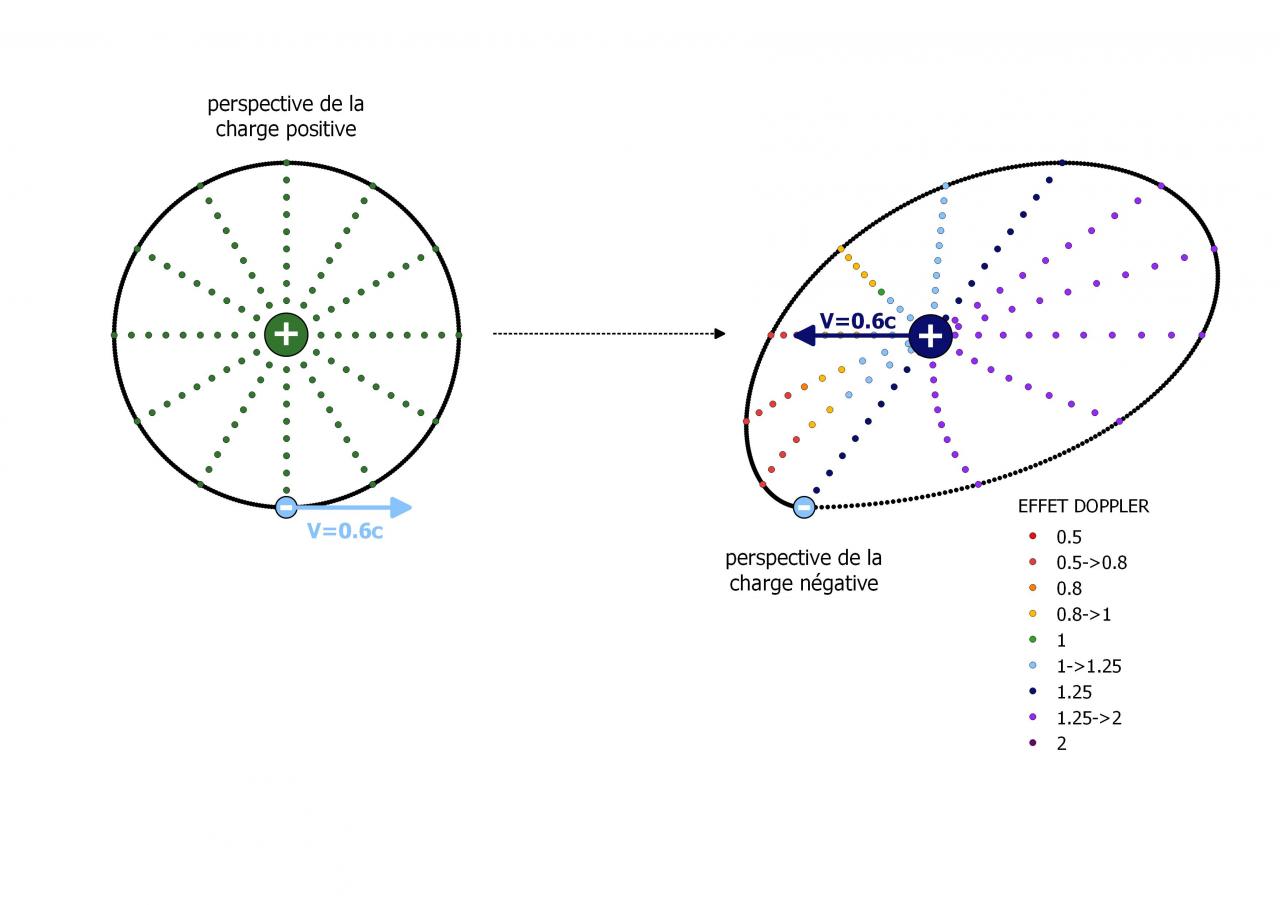
Bonjour,

Imaginons que deux chuteurs O et O' sautent successivement depuis R_max, O' en 1er et O en 2nd.
O' atteint la coordonnée Ro avec une vitesse

Quelques instants plus tard O atteint Ro avec la même vitesse et voit O' atteindre la coordonnée R avec une vitesse

Donc la vitesse relative entre O et O' est

D'ou un schift (EDR) du point de vue de O :

pour avoir le schift total il faut que je divise EDR par le schift gravitationnel (Z + 1) pour tenir compte du décalage d'Eisntein :

Donc :
Si O' émet des photons avec l'énergie E', il seront perçus par O avec une énergie E telle que :

.............................. ............

Je suis donc d'accord avec cette formule même si elle ne représente qu'un cas sur les 4 possibles.
-----

[invite06459106]

Au lieu de dire que tu fais de la RR localement, il faut dire que la géométrie de Minkowski est une bonne approximation localement

La nuance est trop subtile pour moi

Le mot clé (àmha) est "approximation".

Quand l'on dit que localement on peut approximer/assimiler l'espace-temps à du Minkowski, cela exprime que la courbure est un paramètre local, mais l'espace-temps n'est pas plat, mais courbé.
Approximé localement l'espace-temps par Minko, la courbure elle n'est pas approximée par Minko.


-En blabla, ça donne: La courbure en un point exprime l'écart qu'il y a au voisinage en rapport à ce qu'il pourrait se passer si on était chez Minko.
-En moins blabla: Un point A de l'espace-temps, après calcul du tenseur de courbure de l'espace tangent en A, en origine avec sa métrique de Minko, ne donnera pas le tenseur en A, et pourtant c'est le même point.

Pour moi, rien de philo, juste des maths, mais c'est un avis, pas une affirmation..donc à corroborér ou non..Et d'ailleurs je pourrais reformuler sous forme de question, mais l'idée de le faire venant de me venir, et ayant la flemme de recommencer sous forme interrogative je laisse

[Mailou75]

Salut,

Pas l'impression qu'elles soient plus simples que dans les messages précédents. Le texte les explique peut-être mieux. Ou alors tu fais des progrès.

Effectivement, il n'y a ni intégrale ni matrice dans les précédents, mais il y a des notations bizarres (les g_tt etc) qui ne correspondent à rien pour moi, donc je décroche radipement.

Des masses ? Tu ne crois pas si bien dire. Le carré scalaire de la 4-impulsion est la masse au carré ! Cela suffit-il ou alors il y a besoin d'un développement ?

Ben ça pourrait suffire vu que m=0 la 4-impulsion=0 et 0x0xsin(0)=0. Mais je croyais que l'impulsion pour un photon n'était pas p=Y.m.v (matière) mais p=h.f/c (h cst de Planck et f la fréquence) ?
Le vecteur "énergie" représenté ici par exemple (https://forums.futura-sciences.com/a...ml#post6167961) pour un photon n'est il pas justement sa 4-impulsion ? Je ne la vois pas nulle... (je ne dis pas que tu as tort puisque tes calculs n'aboutiraient pas, je cherche où moi je rate un truc...)

Autre possibilité : c'est juste parce l'angle entre lui et lui même est 0 et donc sin(0)=0 suffit à rendre le carré scalaire nul ? Dans ce cas le carré scalaire d'un vecteur est toujours nul ? Finalement t'aurais peut être du pousser les explications, ça m'aurait évité de faire des suppositions douteuses

Bien vu, au point 4, j'ai imposé sans faire attention un photon entrant en prenant P^r positif (parce que a est positif). Pour le cas sortant il faudrait que P^r=-a (P^t demeurant inchangé ). Du coup il y a un signe qui va se ballader. Il faut que je vérifie et que j'ammende mon bilan.

Si tu le dis...

Le problème est qu'il n'est pas sûr que telles méthodes soient efficaces en dehors du cas radial, notamment si ce qui est derrière est mal compris.

C'est même sur qu'elles ne le sont pas ! (sauf orthoradial infinitésimal) Mais je n'ai pas cessé de le répéter : le cas radial où Newton "marche encore" est une porte vers la compréhension, mais n'est pas généralisable à la 2ou3D+t. C'est une "étape" qu'il faut prendre pour ce qu'elle est. Ceux qui en ont les moyens ont tout intérêt à comprendre le général et observer le cas radial comme une "coïncidence".

En y réfléchissant, cela mériterait un fil, et/ou une discussion en privé avec une connaissance commune qui ne vient plus sur le forum. La question n'est peut-être pas si simple. "A t'on le droit de dire qu'en espace temps courbe on peut faire de la RR localement ?" C'est limite philo. On a envie de dire "vous avez 4h".

Arf, comme disait Coluche, la dernière fois que j'ai posé une question, à la fin de la réponse je ne compenais même plus ma question pour ne pas dire que je l'avais oubliée... j'ai d'ailleurs du retard sur ce sujet comme tu le sais et je plaisante c'est très enrichissant, simplement je n'ai que deux mains.

.......

Imaginons que deux chuteurs O et O' sautent successivement depuis R_max, O' en 1er et O en 2nd.
(...)

Je suis donc d'accord avec cette formule même si elle ne représente qu'un cas sur les 4 possibles.

Attention, il n'est plus question de chute libre ici mais uniquement de vitesses aléatoires à deux altitudes différentes. Comme je le disais "si R1 et en dessous de R2 et que Beta positif désigne une vitesse vers le haut alors ces formules fonctionnent". Ca veut dire qu'une vitesse de chute serait un Beta négatif. La formule de mach3 couvre 4 cas sur 8 en fait : B1 et B2 vers le haut, B1 et B2 vers le bas, B1 vers le haut et B2 et vers le bas et enfin B2 vers le haut et B1 et vers le bas, tout ça vu par l'observateur en haut en R2. Pour les 4 derniers cas : la même chose vu depuis R1, il faut une deuxième formule. Rassure toi c'est exactement la même que nous dans le principe : Doppler local en R1 * Doppler local en R2 * Décalage gravitationnel = Shift vu, simplement le décalage gravitationnel s'inverse en changeant d'observateur, il n'est pas réciproque comme le Doppler.

A +

[mach3]

Pour moi, rien de philo, juste des maths, mais c'est un avis, pas une affirmation..donc à corroborér ou non..Et d'ailleurs je pourrais reformuler sous forme de question, mais l'idée de le faire venant de me venir, et ayant la flemme de recommencer sous forme interrogative je laisse

pour moi le côté philo est dans le sens qu'on donne aux mots. Pour ce qui est des maths derrière, toi comme moi savons bien de quoi on parle, mais quand on a une phrase comme "en espace temps courbe on peut faire de la RR localement", on peut la prendre comme vraie ou fausse en fonction du sens qu'on donne à "RR", et les critiques qui pourraient être formulées (dans un sens comme dans l'autre) pourrait très bien s'appliquer à d'autres phrases ou usages courant. Par exemple si on part du principe strict que si l'espace-temps est courbe on ne fait pas de RR, alors on ne fait jamais de RR (sauf au tableau), vu qu'il n'y a nulle part d'espace-temps plat dans le monde réel. Alors faut-il plutôt dire qu'on est dans une situation où la RR est une approximation? qu'on est dans une situation où la géométrie locale est celle de Minkowski mais qu'on ne fait pas de RR pour autant? Pour moi en y réfléchissant c'est des conventions de nommage des choses et des usages voire de la philo (sans que ce soit nécessairement du dénigrement, hein). Après on peut se poser la question sur le fait que telle ou telle façon de dire induit plus ou moins de "misconception" et serait donc plus ou moins souhaitable.

Arrêtons là car cela devient hors-sujet, mais à l'occasion, on pourra en rediscuter ailleurs.

m@ch3

[mach3]

Effectivement, il n'y a ni intégrale ni matrice dans les précédents, mais il y a des notations bizarres (les g_tt etc) qui ne correspondent à rien pour moi, donc je décroche radipement.

Ah oui, je vois. gtt c'est le coeff devant le dt² dans la métrique et grr c'est celui devant dr².

Ben ça pourrait suffire vu que m=0 la 4-impulsion=0 et 0x0xsin(0)=0. Mais je croyais que l'impulsion pour un photon n'était pas p=Y.m.v (matière) mais p=h.f/c (h cst de Planck et f la fréquence) ?
Le vecteur "énergie" représenté ici par exemple (https://forums.futura-sciences.com/a...ml#post6167961) pour un photon n'est il pas justement sa 4-impulsion ? Je ne la vois pas nulle... (je ne dis pas que tu as tort puisque tes calculs n'aboutiraient pas, je cherche où moi je rate un truc...)

Autre possibilité : c'est juste parce l'angle entre lui et lui même est 0 et donc sin(0)=0 suffit à rendre le carré scalaire nul ? Dans ce cas le carré scalaire d'un vecteur est toujours nul ? Finalement t'aurais peut être du pousser les explications, ça m'aurait évité de faire des suppositions douteuses

Considérons une particule de 4-impulsion P qui croise un observateur de 4-vitesse U (). Alors est l'énergie de la particule pour cet observateur et (attention signature +--- sinon il y a des signes qui changent) est l'impulsion (un vecteur) pour cet observateur. Exemple en espace-temps plat et coordonnées de Lorentz pour faire plus simple :





Le carré scalaire de la 4-impulsion en espace-temps plat et coordonnées de Lorentz donne

Avec m la masse. Si E²=p², alors la masse est nulle, sans pour autant que l'énergie et la quantité de mouvement le soit. La norme du vecteur est nulle, il est dit de genre nul, mais le vecteur n'est pas nul. En géométrie euclidienne, seul le vecteur nul possède un carré scalaire nul. En Minkowski, il y a tout un tas de vecteurs non nul dont le carré scalaire est nul, et ils forment les cônes de lumière.

Petite chose amusante, si la masse est non nulle, on peut écrire :

Donc P/m est une 4-vitesse, de coordonnées celle de la particule de 4-impulsion P. Or une 4-vitesse c'est , donc on se retrouve avec :




ce qui rappelle quelque chose... (attention c=1)

m@ch3

[mach3]

Synthèse (v2)

Note : on utilise les coordonnées de Schwarzschild restreintes au cas radial, (t,r), la signature étant (+-). on pose c=G=1.


plus familièrement écrite


1) relation entre coordonnées de la 4-vitesse et vitesse coordonnée
On considère la ligne d'univers d'un objet. En un évènement de coordonnée (t,r) de cette ligne d'univers sa vitesse coordonnée est . Un 4-vecteur u de coordonnées en cet évènement est tangent à la ligne d'univers de l'objet. Son carré scalaire vaut :


La 4-vitesse de l'objet, de coordonnées est elle aussi tangente à la ligne d'univers, elle est donc colinéaire u, c'est à dire qu'on U=ku, et , d'où , soit plus proprement, et

au 4-vecteur précédent, mais son carré scalaire doit valoir 1, c'est à dire que :


On a donc


Les coordonnées de la 4-vitesse sont donc (oui, c'est pas très beau, mais j'ai pas trouvé plus joli pour l'instant...)

2) relation entre 4-vitesse d'un observateur, 4-impulsion d'une particule et énergie
Soit un observateur de 4-vitesse U, coordonnées , et une particule de 4-impulsion P, coordonnées se croisant en un évènement donné. L'énergie de la particule mesuré par l'observateur est :


3) 4-impulsion et vitesse coordonnée d'une particule de genre nul
Si la particule est de genre nul (par exemple un photon), alors le carré scalaire de sa 4-impulsion, tangente à sa ligne d'univers, doit être nul, on a :



Le vecteur p, de coordonnées , avec la vitesse coordonnée de la particule de genre nul, est lui-aussi tangent à la ligne d'univers (il est colinéaire à P) et est donc aussi de genre nul :




4) Transport parallèle de la 4-impulsion d'une particule de genre nul en chute libre
La géodésique de la particule en chute libre est une courbe de paramètre (chaque évènement ayant des coordonnées ) tel que l'équation des géodésiques est satisfaite :


Un vecteur de coordonnées étant tangent à la géodésique.
Cette équation des géodésiques impose que ce vecteur, transporté dans sa propre direction le long de la géodésique, ne doit pas changer (ses coordonnées, oui, mais pas le vecteur lui-même) : il est transporté parallèlement. C'est notamment ce qu'on attend de la 4-impulsion qui doit se conserver localement. Ce vecteur de coordonnées est donc identifiable à la 4-impulsion de la particule de genre nul, à une constante multiplicative près (qu'on peut prendre égale à 1 si on choisit convenablement).

La résolution de la deuxième équation donne la contrainte suivante sur : (pour le détail, se reporter au message 31)
Cela impose la forme suivante pour les coordonnées de la 4-impulsion P : avec a une constante positive. On aura pour un photon sortant et pour un photon entrant

Bilan :
Considérons :
-un observateur émetteur, situé en en l'évènement d'émission, ayant une vitesse coordonnée et de 4-vitesse , dont les coordonnées sont : (oui, c'est toujours pas très beau)
-un observateur récepteur, situé en en l'évènement de réception, ayant une vitesse coordonnée et de 4-vitesse , dont les coordonnées sont : (oh, c'est bon, ça suffit maintenant)
-un photon allant de l'émetteur au récepteur, de 4-impulsion P, dont les coordonnées sont : (r valant à l'émission et à la réception). On note que si , le photon est sortant et et inversement si , le photon est entrant donc

Energie du photon pour l'émetteur :






Autre version qui sera surement utile :


Energie du photon pour le récepteur (même calcul, avec à la place de ) :

Autre version qui sera surement utile :


Rapport des énergies récepteur/émetteur (ou des fréquences, ou inverse des longueurs d'ondes):


Autre version qui sera surement utile :



(lorsqu'il y a des doubles signes, on prend celui du haut si le photon est sortant () et celui du bas si le photon est entrant())

Plus qu'à remplacer les vitesses coordonnées par ce qu'on veut...

Annexe : vitesse de l'émetteur et du récepteur par rapport à des immobiles de Schwarzschild qu'ils croisent au moment de l'émission et de la réception respectivement, donc en et

Un immobile de Schwarzschild en r, a pour 4-vitesse U_0, de coordonnées (U^t_0,0). On a :

Donc

Le facteur , témoignant de la vitesse relative entre un observateur en mouvement, de 4-vitesse U, et cet immobile de Schwarzschild en l'évènement où ils se croisent, est donné par :



On a (non, pas de commentaires, même en annexe, vous commencez à être lourd à la fin!)

Donc



La vitesse relative entre un observateur en mouvement et cet immobile de Schwarzschild en l'évènement où ils se croisent, est donc :
(on note que est positif pour un observateur sortant et négatif pour un observateur entrant)

Le rapport d'énergie du photon entre récepteur et émetteur peut donc se réécrire en fonction des vitesses de l'émetteur et du récepteur relatives à des immobiles de Schwarzschild qu'ils croisent aux évènements d'émission et de réception, respectivement :



Je ne suis pas convaincu de l'utilité de cette dernière formule, mais vu que cela semble vous tenir à coeur, je vous la donne donc en cadeau.

Note de fin : ce post contient surement des coquilles et mérite une relecture approfondie, il se peut que des corrections y soit apportées ultérieurement. Ne pas hésiter à signaler une erreur.

m@ch3

[Mailou75]

Salut,

Considérons une particule de 4-impulsion P qui croise un observateur de 4-vitesse U (...)

Ok. Dejà je suis un boulet... car je ne faisais pas un carré scalaire mais un «carré vectoriel» d’où le sinus... (preuve que je suis allé voir quand même), en prenant le cosinus (1) ça marche tout de suite mieux

Ensuite je vois ce que ça veut dire : Energie totale - impulsion = masse c’est logique c’est la formule E2=m2c4+p2c2, mais l’énergie totale et l’impulsion sont liés à un repère : coordonnée horizontale du vecteur pour l’impulsion et verticale pour l’energie totale. Quand les deux sont egaux E=pc, le vecteur est à 45°, c’est une particule sans masse qui va à c par défaut.

Synthèse (v2)

Ok pour moi

......

Pour passer à la suite (2D+t), j’ai une petite question : la formule de la vitesse orbitale «relativiste» Vorb=racine(GM/(r-Rs)) est elle selon toi une vitesse locale (au même titre que tes dr’/dt’) ? Parce que si c’est le cas, alors c’est exactement ce qu’on attendrait d’elle par etirement qu’un volume d’espace temps de (z+1)r car elle s’ecrit aussi Vorb=(z+1)*Vlib/rac(2) ce qui voudrait dire que Newton continue d’avoir «raison»... ??

Merci

Mailou

[mach3]

Pour passer à la suite (2D+t), j’ai une petite question : la formule de la vitesse orbitale «relativiste» Vorb=racine(GM/(r-Rs)) est elle selon toi une vitesse locale (au même titre que tes dr’/dt’) ? Parce que si c’est le cas, alors c’est exactement ce qu’on attendrait d’elle par etirement qu’un volume d’espace temps de (z+1)r car elle s’ecrit aussi Vorb=(z+1)*Vlib/rac(2) ce qui voudrait dire que Newton continue d’avoir «raison»... ??

J'imagine que tu parles d'une orbite circulaire? A l'arrache comme ça je trouve que (c=G=1, phi et t étant des coordonnées de Schwarzschild), en posant que r ne varie pas et que theta vaut pi/2 et ne varie pas dans l'équation des géodésiques.

Soit V, la 4-vitesse d'un objet en mouvement orbital circulaire. On considère le système de coordonnées (t,r,phi), les coordonnées de V sont , telles que


On sait qu'un 4-vecteur v tangent à la ligne d'univers de l'objet en orbite circulaire peut avoir comme coordonnées , soit donc , car r ne varie pas et la variation de phi est connue. On a :



Posons que v=kV (v et V sont tous deux tangents à la ligne d'univers et donc colinéaires), alors



Donc . Les coordonnées de V sont celles de v divisées par k, donc :

Soit un immobile de Schwarzschild de 4-vitesse U, de coordonnées () (déjà démontré dans un post précédent). Le gamma entre lui et l'objet en orbite circulaire au moment où ils se croisent est :

La vitesse relative est donc :
(au signe près)
ce qui sauf erreur de calcul correspond à ta formule. C'est donc ce que tu appelles une vitesse locale, celle mesurée par l'immobile de Schwarzschild quand l'objet en orbite circulaire le croise.

(je viens vraiment de débloquer un truc dans ma façon d'appréhender les calculs dans l'espace-temps de Schwarzschild depuis quelques jours, c'est très grisant )

m@ch3

[mach3]

Avec ce dont on dispose, on peut calculer le décalage de fréquence entre deux observateurs en orbite circulaire pour peu que l'évènement d'émission et l'évènement de réception soient sur la même radiale (le récepteur doit voir l'émetteur pile au-dessus ou en-dessous de lui).

4-impulsion du photon, P, de coordonnées (photon radial, coordonnée en phi nulle)

4-vitesses et des observateurs émetteurs et récepteurs orbitant en et , de coordonnées et

Energie du photon pour l'émetteur :


Energie du photon pour le récepteur :



Rapport récepteur/émetteur :



Pour un cas plus général, impliquant un photon non radial, il va falloir attendre un peu...

m@ch3

[Mailou75]

Super merci

J'imagine que tu parles d'une orbite circulaire?

Oui bien sur, on commence par les cas simples.

La vitesse relative est donc :
(au signe près)
ce qui sauf erreur de calcul correspond à ta formule.

Ok, parfait merci. Petite rectification, Newton n'a pas tout à fait raison... Si on part des formules de Newton et qu'on applique la même variation locale sur Vlib et Vorb, cad de les diviser par (z+1)_r² alors on obtiendra dr/dt. La vitesse locale ne sera pas celle de Newton mais celle que tu viens de confirmer puisqu'il n'y a pas de déformation spatiale orthoradiale, a priori, juste temporelle.

C'est donc ce que tu appelles une vitesse locale, celle mesurée par l'immobile de Schwarzschild quand l'objet en orbite circulaire le croise.

Je veux bien qu'on change le terme mais ça me semble assez approprié non ?

(je viens vraiment de débloquer un truc dans ma façon d'appréhender les calculs dans l'espace-temps de Schwarzschild depuis quelques jours, c'est très grisant )

Félicitations !
Et je vais pouvoir continuer à te poser plein de questions comme ça (qu'est ce que je peux être opportuniste parfois )

Avec ce dont on dispose, on peut calculer le décalage de fréquence entre deux observateurs en orbite circulaire pour peu que l'évènement d'émission et l'évènement de réception soient sur la même radiale (le récepteur doit voir l'émetteur pile au-dessus ou en-dessous de lui).

Humm, pas d'accord sur l'énoncé. Si on considère que c'est le photon qui a une trajectoire radiale alors les objets ne se "verront" pas sur la radiale. Voir exemple plus bas *

Rapport récepteur/émetteur :

Pour un cas plus général, impliquant un photon non radial, il va falloir attendre un peu...

Ok, c'est bien la variation de fréquence reçue par R2.

Pour ma part j'applique la logique suivante, si R1 est en dessous de R2, R1 est l'observateur:
- Un immobile en R1 voit un voyageur en orbite en R2 avec un Doppler transverse (cette fois...) redshift Y₂
- Un voyageur en orbite à R1 voit un immobile en R2 avec un effet d'aberration blueshift 1/Y₁
* le rayon radial sera vu projeté vers l'avant du fait de l'aberration, pas perpendiculairement au déplacement orbital (ça nous fait déjà un point vu, plus qu'une infinité et c'est bon )
- Donc un voyageur en orbite à R1 voit un voyageur en orbite à R2 avec un shift Y₂/Y₁
- Ensuite on applique le décalage gravitationnel entre R2 et R1, blueshift (z+1)₂/(z+1)₁
et on trouve un shift total blueshift :



Cette formule donne exactement les même résultats que la tienne (à part que moi c'est longueur d'onde z+1 et toi fréquence) et il se trouve que cette fois c'est entièrement réciproque !!
Si R1 voit R2 avec un blueshift 1/z+1 c'est que R2 voit R1 avec un Redshift z+1 inverse.
Du coup je comprends pourquoi tu n'as qu'une formule

Pour un cas plus général, impliquant un photon non radial, il va falloir attendre un peu...

C'est la prochaine étape il me semble, je ne vas pas t'être d'une grande aide... pas de stress sur le délai, je prends le train ce soir

A bientôt, encore mercii pour tout

Mailou

[mach3]

Humm, pas d'accord sur l'énoncé. Si on considère que c'est le photon qui a une trajectoire radiale alors les objets ne se "verront" pas sur la radiale.

oui, tu as raison, fichue aberration!

m@ch3

[Zefram Cochrane]

Bonjour,
Normalement, tu devrait aboutir à ceci :


c'est à dire un décalage pour le Soleil de 20 seconde d'arc par rapport à l'axe perpendiculaire à la vitesse.

[Mailou75]

Salut Zef,

Normalement, tu devrais aboutir à ceci :

Non, on a déjà parlé de ce dessin ailleurs. C’est de l’aberration pour une vitesse «faible» en espace plat : tous tes rayons lumineux sont droits or en RG seul un rayon radial sera droit, tous les autres seront courbes. On ne peut pas dessiner ce qui est «vu» (et encore moins «comment» c’est vu) tant qu’on ne connait pas les trajectoires des rayons lumineux incidents, c’est peine perdue...

[Mailou75]

PS : le seul truc qu’on pourrait faire à la limite c’est représenter le «comment», car il existe des formules pour les déviations en plan des rayons lumineux. Seulement on ne saura pas ce qui est vu (en terme d’évènements), l’interet est donc limité.

[Zefram Cochrane]

Salut Mailou

Non, on a déjà parlé de ce dessin ailleurs. C’est de l’aberration pour une vitesse «faible» en espace plat : tous tes rayons lumineux sont droits or [/B]en RG seul un rayon radial sera droit[/I], tous les autres seront courbes. On ne peut pas dessiner ce qui est «vu» (et encore moins «comment» c’est vu) tant qu’on ne connait pas les trajectoires des rayons lumineux incidents, c’est peine perdue...

C'est bien du rayon radial dont je parlais.

Peut-être obtiendrais ton quelque chose dans ce goût là pour les autre rayons.

[Zefram Cochrane]

Bonjour,
J'ai une question:
On prend Ro = Rmax.
Soit O stationnaire en Ro d'un TN et O' un chuteur plongeant dans le TN depuis Ro avec une vitesse µ ; µ pouvant être supérieure à la vitesse de libération.
On a pour une chute libre depuis Ro avec µ = 0

la vitesse locale du chuteur est-elle : ?
Ceci impliquerait que vu par un obsrvateur stationnaire à Roo du TN sur la même radiale du chuteur la vitesse coordonnée serait:
avec
Donc si je pose la vitesse coordonnée du chuteur serait ?

[Zefram Cochrane]

Bonjour,
J'ai une question:
On prend Ro = Rmax.
Soit O stationnaire en Ro d'un TN et O' un chuteur plongeant dans le TN depuis Ro avec une vitesse µ ; µ pouvant être supérieure à la vitesse de libération.
On a pour une chute libre depuis Ro avec µ = 0

la vitesse locale du chuteur est-elle : ?
Ceci impliquerait que vu par un obsrvateur stationnaire à Roo du TN sur la même radiale du chuteur la vitesse coordonnée serait:
avec
Donc si je pose la vitesse coordonnée du chuteur serait ?

normalement, aucun pb avec les signes -
doublon avec le mess précédent

[Mailou75]

Salut,

C'est bien du rayon radial dont je parlais.

Alors pourquoi tu dessines toute la patatoide ? C’est hors sujet.

On prend Ro = Rmax

la vitesse locale du chuteur est-elle : ?

Non, la formule d’une chute depuis Rmax avec une vitesse initiale supérieure à la Vlib locale n’existe pas. Calvert avait donné la formule pour un tel cas classique mais elle n’est pas applicable en relativité. Certains s’y sont essayé (un illuminé en qui personne ne croit et une equipe de deux mais qui n’a pas entierement convaincu...). Je n’ai ni les formules ni les noms des mecs sous la main mais c’est sur que c’est pas si simple que ta formule, dsl.

A +

Mailou

[Zefram Cochrane]

Salut,
Si tu regardes le rayon radial passant par l'électron il est bien droit dans la perpective de l'électron et les autres ne passant pas par lui sont vus courbes dans sa perspective. Donc on ne sait pas si ce shéma est incorect ou pas.

Pour ce qui est de la chute libre avec vitesse initiale > Vlib, je ne vois pas pourquoi la formule serait fausse
On sait que pour R=Rs , beta = 1 et ce quel puisse être Ro (Rmax) de départ.
donc si en Ro (Rmax), O' a déjà une vitesse u et donc une énergie E(µ) = mc² * Y(µ) alors en R il a une énergie E(w) avec w la vitesse donné par la loi de composition des vitesse µ et beta. Je ne vois pas ou est l'erreur.

[Mailou75]

Donc on ne sait pas si ce shéma est incorect ou pas.

Si on sait, il est juste pour la radiale (et encore...) et faux pour tout le reste. Sinon a quoi sert la RG..?

Pour ce qui est de la chute libre avec vitesse initiale > Vlib, je ne vois pas pourquoi la formule serait fausse
On sait que pour R=Rs , beta = 1 et ce quel puisse être Ro (Rmax) de départ.
donc si en Ro (Rmax), O' a déjà une vitesse u et donc une énergie E(µ) = mc² * Y(µ) alors en R il a une énergie E(w) avec w la vitesse donné par la loi de composition des vitesse µ et beta. Je ne vois pas ou est l'erreur.

Je comprends la logique mais la relativité n’est pas logique... si le sujet fait débat c’est que Zef a tort, à priori. L’illuminé c’est Mizonny et les autres Martel et Poisson, regarde ce qu’ils ont fait

Si tu veux tester ta formule, essayes déjà avec Vlib tu verras qu’a Rmax-epsilon tu ne seras plus à la Vlib locale (Rmax-epsilon). Ça devrait suffire...

[Zefram Cochrane]

Salut,
j'ai fait des tests et il s'avère qu'effectivement la loi de composition de la RR ne fonctionnent pas en RG.
Je ferais des recherches voir si je trouve quelque chose de sympa.

[mh34]

Fil transféré en section "discussions libres".

[Mailou75]

Salut,

J'ai un problème avec les shifts perçus par les observateurs en orbite.

Rapport récepteur/émetteur :

Pour ma part j'applique la logique suivante, si R1 est en dessous de R2, R1 est l'observateur:
- Un immobile en R1 voit un voyageur en orbite en R2 avec un Doppler transverse (cette fois...) redshift Y₂
- Un voyageur en orbite à R1 voit un immobile en R2 avec un effet d'aberration blueshift 1/Y₁
* le rayon radial sera vu projeté vers l'avant du fait de l'aberration, pas perpendiculairement au déplacement orbital (ça nous fait déjà un point vu, plus qu'une infinité et c'est bon )
- Donc un voyageur en orbite à R1 voit un voyageur en orbite à R2 avec un shift Y₂/Y₁
- Ensuite on applique le décalage gravitationnel entre R2 et R1, blueshift (z+1)₂/(z+1)₁
et on trouve un shift total blueshift :

Les deux versions donnent le même résultat, y'a des chances pour que ce soit juste, pourtant quand j'essaye de me représenter tout ça je tombe sur des incohérences. Je vais essayer d'expliquer le problème aussi clairement que possible…

RAPPEL : On a deux orbites en R1 et R2. R2 est au dessus de R1. J'utilise la notation (z+1)_r = 1/racine (1-Rs/r)

1 - Un observateur statique en R1 va voir un immobile en R2 avec un blueshift (z+1)₂/(z+1)₁
(inversement celui en R2 verrait l'immobile en R1 avec un redshift (z+1)₁/(z+1)₂)
Rien de neuf jusqu'ici.

2 - Un observateur immobile en R2 va "voir" un voyageur en orbite en R2 redshift valant Y₂ (le gamma lié à la vitesse orbitale en R2).
Je mets "voir" entre guillemets car il s'agit du croisement idéalisé pour Doppler transverse.

Donc 1+2 donne : Un observateur immobile en R1 voit un voyageur en orbite en R2 avec un shift Y₂ * (z+1)₂/(z+1)₁.

3 - Ajoutons un voyageur en orbite en R1, mais conservons pour l'instant le point de vue de l'immobile en R1.
Il voit : le voyageur en R1 compressé orthoradialement de 1/Y₁ , l'immobile en R2 étiré radialement de (z+1)₁/(z+1)₂ l'inverse du blueshift et le voyageur en R2 étiré radialement de (z+1)₁/(z+1)₂ et compressé orthoradialement de 1/Y₂. Jusqu'ici tout va bien…

Demandons nous maintenant ce que va voir le voyageur en R1. J'ai parlé d'aberration mais finalement j'ai de gros doutes… Appliquer ce principe reviendrait à dire qu'on prend l'image de ce qu'observe l'immobile en R1 et qu'on la transforme. Les deux observateurs en R2 seront donc tous les deux vus projeté vers l'avant et dilatés orthoradialement MAIS : l'immobile en R1 voyait le voyageur en R2 compressé orthoradialement par rapport à l'immobile en R2. Donc la déformation de l'aberration va étirer cette image mais en conservant les proportions : le voyageur sera toujours plus compressé que l'immobile.

J'en arrive donc au sujet…. Ceci satisfait les calculs mais ne me convient pas du tout dans le principe. Pour observer réellement ce que voit le voyageur en R1 il faudrait changer de repère (ce qui n'est pas aisé en RG, humm…). Par changement de repère, il verrait les immobiles en R1 et R2 compressé orthoradialement de Y₁ mais le voyageur en R2 aurait cette fois une vitesse relative moindre (quasi nulle si les orbites sont proches et donc les vitesses quasi égales) donc il devrait voir le voyageur en R2 moins compressé que l'immobile en R2 qui a alors une grande vitesse relative.

En clair, si le changement de repère en RR explique l'aberration, on ne peut pas l'appliquer ici car les cônes passés ne sont pas "droits". Le fait que le dernier facteur à appliquer obtenir le shift reçu par le voyageur en R2 soit 1/Y₁ n'est donc pas du à l'aberration mais à la vitesse relative des observateurs en orbite. Enfin je ne sais pas je suis un peu perdu...

J'ai des scrupules à mettre tout ça en image parce que c'est potentiellement faux… c'est pourquoi j'aimerais d'abord faire le point.

Merci d'avance

Mailou

[Mailou75]

Par changement de repère, il verrait les immobiles en R1 et R2 compressés orthoradialement de Y₁ mais le voyageur en R2 aurait cette fois une vitesse relative moindre (quasi nulle si les orbites sont proches et donc les vitesses quasi égales) donc il devrait voir le voyageur en R2 moins compressé que l'immobile en R2 qui a alors une grande vitesse relative.

Mea culpa, this is bullshit !

J’ai regardé hier soir pour la RR et, contre intuitivement comme d’hab, dans le cas présent, le fait d’avoir une vitesse relative moindre n’empêchera le voyageur en R2 d’être vu plus compressé que l’immobile en R2. L’ensemble serait donc cohérent, mettant en évidence deux modes de conservation des volumes d’espace temps : propres à l’objet ou propres à ce qui est vu, valant en RR comme en RG. Cela signifie aussi que le voyageur en orbite en R1 va prendre l’image de ce que voit l’immobile en R1 (en faisant fi de la courbure des rayons lumineux - vitesse lumière - et de la cause des déformations vues par l’immobile en R1) comme une base sur laquelle appliquer simplement l'aberration correspondant sa vitesse orbitale.

Bref, j’imagine que ce n’est pas forcément très clair... j’ai quelques schémas à produire/clarifier si ça vous intéresse.

A plus

Mailou

[Mailou75]

Comment un voyageur en orbite voit-il un autre voyageur en orbite ?

C'est la question à laquelle on a commencé de répondre avec mach3. J'ai essayé de mettre tout ça en images...

On va commencer par rappeler les formules. En classique la vitesse de libération vaut Vlib=racine(Rs/r) et la vitesse orbitale vaut Vorb=Vlib/racine(2). En relativiste la vitesse orbitale vaut V=Vorb*(z+1)_r où (z+1)_r=1/racine(1-Rs/r). En gros la vitesse orbitale locale est égale à la formule de Newton multipliée par le (z+1)_r local, c'est à dire l'effet Einstein.

On va prendre deux objets Rouge et Bleu en orbite à respectivement R₁=1,71Rs et R₂=2,97Rs et on va les représenter en coordonnées de Schwarzschild. Mais l'observateur éloigné (noté infini) va faire l'opération inverse et diviser la vitesse par le (z+1)_r puisque tout ce qu'il voit est ralenti. Donc on peut dire que pour l'observateur éloigné la formule de Newton fonctionne et il voit une vitesse dr/dt=dr/dT=Vorb=racine(Rs/2r). En chiffres ça donne :

.............................. ........... R₁ ............ R₂

Vitesse classique ...... V ...... 0,540c ..... 0,410c
Vitesse relativiste ..... B ...... 0,838 ....... 0,504
Facteur de Lorentz .... Y ...... 1,833 ....... 1,157
Effet Einstein ........ z+1 ...... 1,551 ....... 1,228

Et nous pour l'instant on va surtout s'intéresser aux premiers chiffres, la vitesse classique valable en Schw pour dessiner. Ensuite on va vérifier que la logique mise en place fonctionne. L'observateur éloigné voit les voyageurs en orbite avec un shift multipliant leur Y local et le (z+1)r local, soit :

Shift perçu à l'oo ... z+1 ...... 2,843 ...... 1,421

Ce décalage va nous permettre de placer des intervalles de temps propre réguliers le long des trajectoire. C'est la valeur de l'intervalle vertical. Enfin on va vérifier la valeur du shift perçu par le voyageur en orbite en R₁ quand il regarde celui en R₂. Il le voit avec un Doppler transverse Y₂ + un effet Einstein (z+1)₂/(z+1)₁ + un effet d'aberration 1/Y1 soit un total, formule déjà donnée :



C'est donc un blueshift valant z+1=0,5. Et c'est bien ce que nous dit le repère de Schw : Rouge va recevoir 4s images de Bleu en 2s (je dis seconde pour arranger c'est comme d'hab on règle le 0,1.Rs/c qui va bien...). Mais pas exactement, parce que les trajectoires sont purement radiales et que les vitesses angulaires de Rouge et Bleu ne sont pas les mêmes donc ils ne peuvent s'envoyer deux photons radiaux de suite. J'ai donc représenté un deuxième Bleu... mais ça ne change rien, on peut toujours imaginer deux photons envoyés avec un intervalle de temps infinitésimal ou simplement que le photon lui même est blueshifté. Bref, pour ma part, pour une première vérif, ça me convient...

[Mailou75]

La deuxième partie est une parenthèse de RR pour régler un sujet sur l'aberration et plus si affinités…

On transpose le sujet avec des mouvements rectilignes uniformes : Vert foncé et Vert clair sont des immobiles espacés d'une distance R₂-₁. Rouge a une vitesse B₁=0,838 et Bleu une vitesse B₂=0,504, par rapport aux immobiles (voir tableau précédent).

Vert foncé voit Bleu avec un Doppler transverse Y₂=1,157 et une vitesse apparente B₂=0,504. Attention, la notion introduite ici n'est pas anodine, elle est même au centre du sujet : c'est la distance parcourue entre deux images successives / temps propre de l'observateur, littéralement la vitesse à laquelle un observateur voit évoluer un objet en fonction de son temps propre.

Elle vaut simplement v=B.Y/(z+1) où (z+1) est le shift vu [une démonstration rigoureuse serait bienvenue] Dans l'exemple précédent ça donne v=B₂.Y₂/Y₂=B. Vert clair est évidement vu sans vitesse ni shift puisqu'il est immobile par rapport à Vert foncé.

Quand on passe dans le repère de Rouge, ce sont Vert foncé et Vert clair qui avancent vers lui à B₁=0,838. Bleu a cette fois une vitesse ₃= "0,838-0,504" = 0,578 (opération relativiste). On voit à l'intersection avec l'espace que Bleu est moins compressé que Vert clair, car sa vitesse par rapport à Rouge est moindre, pour autant [c'est ce qui me questionnait...] Bleu est vu plus compressé radialement que Vert clair.

Pour le détail numérique :
- du fait de l'aberration, Rouge voit Vert clair avec un blueshift z+1=1/Y₁=0,545
- du fait de l'aberration, Rouge voit Bleu avec un blueshift z+1=Y₂/Y₁=0,631
- la vitesse apparente de Vert clair est v=B₁.Y₁/0,545=2,817c
- la vitesse apparente de Blau est v=B₃.Y₃/0,631=1,123c (Y₃=1,226)

Mais je n'ai pas fait tout ça juste pour le plaisir d'un nième dessin sur l'aberration… Le long des trajectoires de Rouge et Vert foncé dans le dessin de droite j'ai représenté des petits volumes en pointillé. Ce sont des volumes synchronisés pour ces voyageurs et sont égaux par changement de repère. C'est une règle de conservation pour l'espace-temps de Minkowski.

Mais… ce qui est étonnant c'est que dans la partie haute du dessin les volumes vus sont eux aussi contraints à une conservation du volume. L'aberration va étirer d'autant visuellement les objets (Y) qu'elle va les accélérer avec le blueshift (1/Y). Plus un volume est plat (<1) plus c'est signe de blueshift, inversement plus ile est étiré en hauteur (>1) plus ce sera un redshift. Tous les volumes vus représentés sont donc égaux, mais Magritte nous dirait "ceci n'est pas une repère"... de la même façon que "l'anisotropie de la vitesse de la lumière dans un repère tournant" est une ineptie puisqu'il est question du même genre de "repère" montrant ce qui est vu. Malgré cela, c'est ce que va faire Schwarzschild !

[Mailou75]

Revenons à la RG. Au départ, rien de neuf par rapport à ce qui a été dit dans ce fil, je vais juste faire le tour des chiffres…

1) Dans la figure de droite on est en coordonnées (r;t) c'est l'observateur éloigné de Schw. Il voit Vert foncé en R₁ avec un redshift (z+1)₁=1,551 et Vert clair en R₂ avec un reshift (z+1)₂=1,228 (voir tableau). Il les voit compressés radialement du facteur inverse.

Il voit Rouge avec un redshift Y₁*(z+1)₁=2,843 et Bleu avec un redshift Y₂*(z+1)₂=1,421 (on remarque que l'un est le double de l'autre). Et on retrouve les vitesses apparentes de la première figure V₁=0,540c et V₂=0,410c. Rouge et Bleu sont à la fois compressés radialement par l'effet Einstein ET compressés orthoradialement par la RR !

2) Ensuite on change de repère et on passe chez Vert clair. Il voit Bleu avec un Doppler transverse, cad sa vraie vitesse locale B₂=0,504 et son gamma Y₂=1,157 (voir tableau). Il est aussi compressé de 1/Y₂.

Il voit Vert foncé avec un redshift (z+1)₁/(z+1)₂=1,263, compressé radialement du facteur inverse. Et il voit Rouge avec un redshift Y₁*1,263=2,315 et une vitesse apparente v=B₁Y₁/2,315=0,663c

3) Puis chez Vert foncé, qui voit Rouge avec un Doppler transverse etc... B₁=0,838 et Y₁=1,833 (voir tableau).
Il voit Vert clair avec un blueshift (z+1)₂/(z+1)₁=0,792, étiré radialement du facteur inverse.
Il voit Bleu avec un blueshift Y₂*0,792=0,917 et une vitesse apparente v=B₂Y₂/0,917=0,636c

4) Nous voilà au bout du chemin… on change "partiellement" de repère pour savoir ce que voit Rouge. Vert a un mouvement réciproque et Rouge le voit avec un Doppler transverse etc... B₁=0,838 et Y₁=1,833 et compressé de 1/Y₁.

Enfin, il voit Vert clair et Bleu projetés vers l'avant du fait de l'aberration et qui s'approchent de lui. Et là on va récupérer les données du deuxième exercice et leur appliquer l'effet Einstein de R₁ vers R₂ soit 0,792. Rouge voit donc :

- Vert clair avec un blueshift z+1=0,545*0,792=0,432
- Vert clair avec une vitesse apparente v=2,817/0,792=3,558c
- Bleu avec un blueshift z+1=0,631*0,792=0,5 << c'est ce qu'on cherchait !!
- Bleu avec une vitesse apparente v=1,123/0,792=1,419c

A nouveau, TOUS les volumes de la figure sont égaux. De la pate à modeler d'espace temps, déformable mais incompressible. Vous me direz qu'une fois qu'on a fixé la surface (vue) et la hauteur (shift) d'un volume, son inclinaison (vitesse apparente) n'a aucun impact. C'est juste… mais si le calcul de mach3 est correct (pour les fréquences reçues) alors d'une façon ou d'une autre la surface vue doit être étirée, si on veut respecter la règle de conservation des volumes d'espace-temps vus. J'avoue être un peu sceptique sur ce résultat qui me parait "trop simple" mais il a au moins le mérite d'être cohérent.

J'en arrive donc à ma conclusion : soit la RG ne s'intéresse qu'au résultat vu (dans un "repère" qui n'en est pas vraiment un) et à ce moment là il manque l'Explication, la partie immergée de l'iceberg, l'équivalent RR du cone passé et des volumes pointillés de la deuxième figure, SOIT… Schw de par son choix de (r;t) traduit une infime partie de la RG en ne traitant que le résultat pour l'observateur à l'infini. Je suppose que c'est la deuxième réponse et que je n'ai pas fini d'en baver…

Merci à tous ceux qui ont eu le courage de lire jusqu'ici
Merci d'avance pour vos réponses

Mailou

[Mailou75]

Salut,

En relisant je me rends compte que j'ai omis quelques détails :
- Dans le repère de Vert clair, il voit l'observateur à l'infini avec un blueshift 1/1,228=0,814 et étiré radialement du facteur inverse
- Dans le repère de Vert foncé, il voit l'observateur à l'infini avec un blueshift 1/1,551=0,645 mais j'imagine que vous aviez compris (si on prend le volume Vert foncé dans le repère de Gris à l'infini et qu'on le couche sur le coté, on obtient le volume Gris dans le repère de Vert foncé)
- Un point amusant : si on ne parle pas d'évolution future (cad de la pente des volumes vus) alors si Bleu tournait dans le sens inverse, Rouge verrait pourtant exactement la même chose !! Je ne pourrais pas le démontrer mais ça se comprend car les relations sont uniquement radiales (Doppler transverse et aberration) donc seul le Y intervient (pas le z+1 Doppler qui donne un sens au mouvement).
- Enfin, @ mach3 : si tu passes par là, je ne suis pas contre un "coup de tampon"

Merci

Mailou

[Mailou75]

Salut,

Pour m'occuper en attendant de résoudre le problème de "K" dans lequel vous m'avez plongé… et pour essayer de donner une image parlante de ce qu'est la parabole de Flamm, abordée au message 56 sans plus de précision.

Attention ce n'est pas un repère. La parabole a pour équation :



C'est une longueur propre : le somme de toutes le longueurs propres locales, la longueur d'une corde tendue entre r et Rs. Par exemple, comme montré sur la figure de gauche, un intervalle propre Δd sera vu par un observateur à l'infini comme un intervalle Δr. Cet intervalle n'est pas forcément infinitésimal.

La figure montre qu'une longueur propre de d=7 mètres (ou km ou années lumière peu importe c'est proportionnel, tout dépend de la valeur qu'on donne à Rs, ici 1m) sera vue par l'observateur à l'infini comme une longueur r=5 mètres (6-1). La parabole peu donc être découpée en 7 tronçons égaux marqués par les verticales grises.

Pour que ceci soit plus clair, j'ai représenté des billes, toutes équivalentes et collées les unes aux autres depuis Rs "sur l'espace" de longueur propre qu'est la parabole. Elles seront vues de plus en plus compressées à l'approche de Rs par l'observateur éloigné de Schwarzschild. Finalement c'est sur cet intervalle proche de Rs que les déformations seront les plus flagrantes, on voit qu'au delà de r=6 il va presque voir des cercles, presque…

A droite, j'ai ajouté une dimension pour obtenir la "paraboloide de Flamm" (plus connue sous ce nom d'ailleurs). De la même façon j'ai disposé sur un quart de cercle des billes cote à cote. La projection en dessous n'est pas exactement "ce que va voir l'observateur à l'infini" mais "ce que verront radialement des observateurs à l'infini disposés en quart de cercle" (compte tenu de la courbure des rayons lumineux, ce qui est effectivement vu est un poil plus compliqué et je ne sais pas encore le faire, clin d'œil a mach3 qui a du pain sur la planche ).

Par contre ce que dit cette figure 2D+z, c'est que la paraboloïde représente vraiment la "surface propre" d'espace : les billes disposées dessus ont toutes un rayon propre égal. Donc :

- Si un observateur arpente (doucement) l'espace radial entre r=6 et r=Rs, il trouvera que la longueur propre (7m) ne correspond pas à ce qu'il voyait en partant de sa position éloignée (~infini)

- Si ce même observateur arpente l'espace orthoradial, c'est à dire qu'il tourne autour du trou noir à une distance constante du centre du trou noir, et qu'il mesure une circonférence C une fois qu'il a fait un tour, alors il trouvera que la formule C=2*Pi*r tombe juste avec le r qu'il voyait quand il était éloigné (~infini).

Je crois que c'est ce que mach3 et Amanuensis appellent le "rayon aréolaire" : La surface d'une sphère concentrique au trou noir a une surface propre qui correspond bien à ce qui est vu depuis l'infini (r) alors que la mesure réelle de la longueur propre du rayon (d, si tant est qu'on mesure de l'espace en dessous de Rs…) nous dirait que la formule géométrique classique est fausse.

Voilà, ceci m'aide à mettre les idées au clair et j'espère que ça vous sera aussi profitable.
Deedee va encore me dire que je me sers du Forum comme d'un blog mais je n'y peux rien si je n'ai pas eu de réponses aux derniers messages. J'espérais que cela vous intéresse et aussi une validation… en même temps si ça avait du être faux, je le saurais déjà je pense

Merci d'avance de ne pas fermer le fil pour cause de monologue, il me reste encore un dernier schéma à poster pour conclure ce fil

Mailou

NB : Les couleurs n'ont rien à voir avec un shift, toutes les billes sont vues redshiftées par l'observateur éloigné (la rouge est quand même plus redshiftée que la violette)

[mach3]

Je crois que c'est ce que mach3 et Amanuensis appellent le "rayon aréolaire" : La surface d'une sphère concentrique au trou noir a une surface propre qui correspond bien à ce qui est vu depuis l'infini (r) alors que la mesure réelle de la longueur propre du rayon (d, si tant est qu'on mesure de l'espace en dessous de Rs…) nous dirait que la formule géométrique classique est fausse.

c'est exact. C'est d'ailleurs une façon de définir r sans faire référence à une distance au centre, que ce soit en région I ou II : l'ensemble des évènements ayant le même couple r,t est une sphère de surface 4\pi r^2 (en fait deux sphères si on compte les régions III et IV de la géométrie complète). Si on laisse t libre, en région I on a une sphère statique, autrement dit un cylindre sphérique dont la génératrice est de genre temps, et, en région II, on a un espace 3D en forme de cylindre sphérique (et cet espace évolue à mesure que r, coordonnée temporelle dans ce cas, change).

désolé de ne pas plus participer à ce fil, la concentration nécessaire me demanderait un temps dont je ne dispose pas en ce moment.

m@ch3