Trou noir et chute libre : application numérique

[mach3]

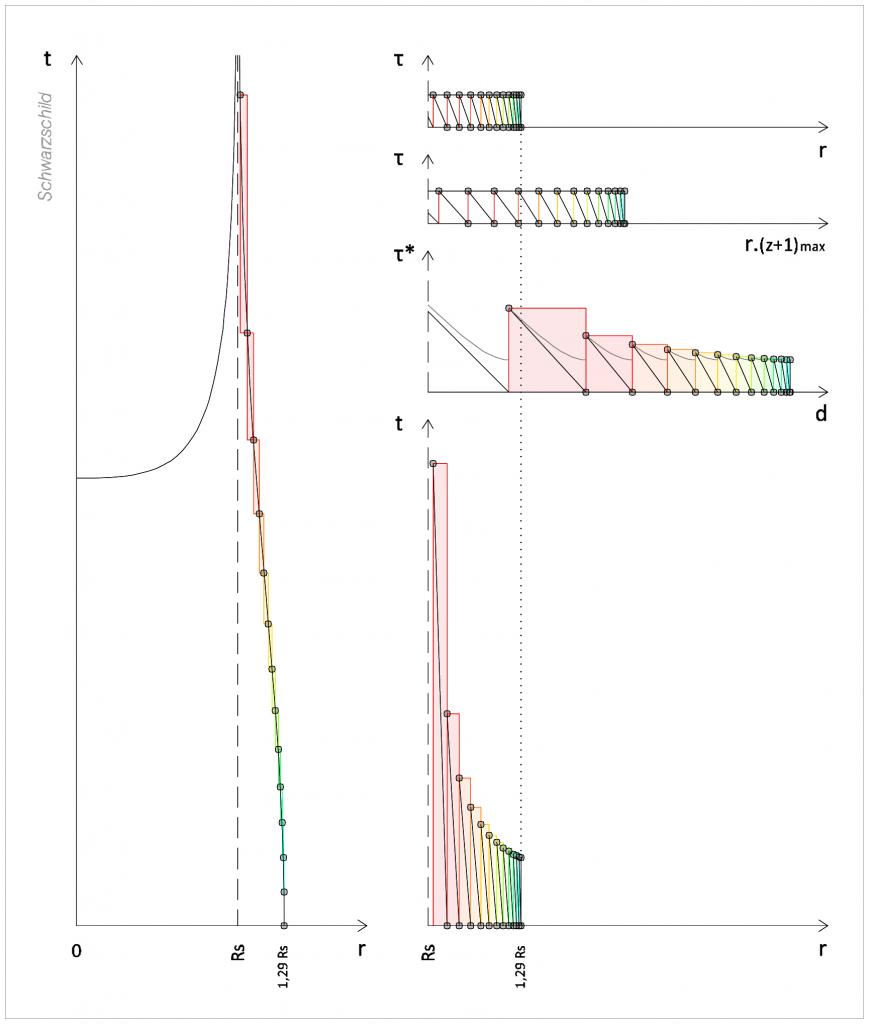
Bon, j'avais jamais exploré ça et je dois dire que c'est joli.

Toujours en 1+1D.

On va s'intéresser à la ligne d'univers d'un photon de trajectoire radiale dans l'espace-temps de Schwarzschild : une géodésique radiale de genre nul.

On peut décrire cette géodésique comme une courbe paramétrée, chaque événement la composant ayant ses coordonnées (dans le système de coordonnées (t,r) de Schwarzschild) données par des fonctions monotones d'un paramètre (qui n'est pas la longueur d'onde) : . Ce paramètre n'est pas encore spécifié, on sait juste qu'il varie de façon monotone le long de la géodésique.
Un vecteur en un événement donné de la géodésique, dont les coordonnées sont de la forme , sera tangent à la géodésique.

Le photon dont c'est la géodésique porte une 4-impulsion P, de coordonnées . Ses coordonnées sont telles que si on a un observateur qui réceptionne le photon (il le croise) et que sa 4-vitesse U à pour coordonnées , alors il va mesurer que le photon a une énergie :



En chaque événement de la géodésique nulle, il y a un 4-vecteur , tangent à la géodésique. On peut considérer que le paramètre , qui n'est pas encore spécifié, est tel qu'on a justement :


Comme il est tangent à une géodésique nulle, il doit lui-même être de genre nul. Son carré scalaire via la métrique doit être nul. On a :

D'où


On obtient donc la vitesse coordonnée de cette géodésique radiale :

(signe à choisir selon entrant ou sortant)

Au passage, une petite intégration nous donne (signe à choisir selon entrant ou sortant et définition à une constante additive près), la fonction qui décrit la géodésique dans un repère (t,r), mais cela ne nous sera pas très utile.

Cette 4-impulsion P est transportée parallèlement à elle-même le long de la géodésique radiale, et on sait qu'elle doit se conserver localement, c'est à dire que si je me place en un évènement de la géodésique de paramètre , qui porte une 4-impulsion , que je transporte cette 4-impulsion en un évènement de la géodésique de paramètre (avec arbitrairement petit), qui porte une 4-impulsion et que je soustrait cette dernière à celle que je viens de transporter, je dois obtenir 0.
Formellement, la dérivée covariante de P dans la direction de P est 0, en langage abstrait : . C'est l'équation des géodésiques, qui en coordonnées de Schwarzschild est le couple (cas radial, donc pas de composantes angulaires) :




Elle est construite à partir des coefficients de Christofell, qui décrivent la connexion. Contrairement à d'autres cas où cette équation sert à trouver r et t et où est le temps propre, ici r et t sont connus (merci à la métrique) et il nous faut trouver un candidat pour (qui ne peut pas être le temps propre). On va tout multiplier par :




et ça donne :









Considérons d'abord l'équation radiale (la seconde). On sait que n'est pas nul, car le paramètre doit évoluer le long de la géodésique alors que t varie, donc on en déduit que . On a donc un tel que :



En effet, on aura et

Réécrivons l'équation temporelle (la première) et faisons apparaitre les dérivées de r :















Elle est bien vérifiée, est bien contraint par

Reste à trouver "a" (parce b on s'en fiche, c'est juste une définition de l'origine sur la géodésique et ça disparait dès qu'on dérive). Revenons à la 4-impulsion, qu'on peut maintenant noter P(r), r étant devenu un paramètre acceptable pour notre géodésique, elle était de coordonnées . Avec les développements précédents, nous pouvons les préciser :




Considérons un immobile de Schwarzschild, se maintenant en r. Sa 4-vitesse U à pour coordonnées (coordonnée radiale nulle car pas de mouvement suivant r). D'abord il nous faut trouver . On sait que le carré scalaire via la métrique doit nous donner 1 pour une 4-vitesse. On a :





Enfin l'énergie du photon sera pour l'observateur considéré :

.

Cela fixe la valeur de a : si un immobile de Schwarzschild situé en r mesure une énergie E, alors


Mais bon, la valeur de a n'est pas si importante, car ce sont les rapports d'énergies mesurées par différents observateurs qui nous intéressent pour le redshift. En effet, un autre observateur, en r' avec une 4-vitesse U', mesurera une énergie E' :
.

Le rapport entre E et E' est le rapport des fréquences, donc le rapport inverse des longueurs d'ondes. L'effet Einstein (shift entre observateurs immobiles de Schwarzschild) sera donc donné par :

Ce qui est bien ce qu'on attendait!

On peut ensuite passer au cas le plus général, où les deux observateurs sont en mouvement quelconque...

m@ch3
-----

[yves95210]

(...)

Le rapport entre E et E' est le rapport des fréquences, donc le rapport inverse des longueurs d'ondes. L'effet Einstein (shift entre observateurs immobiles de Schwarzschild) sera donc donné par :

Ce qui est bien ce qu'on attendait!

(intervention inutile, juste pour dire que je n'ai pas complètement déserté ce forum, et que je vous suis... de loin)

[Mailou75]

Salut et merci,

Petit développement, qui, je l'espère, élèvera la compréhension. (...)

J'arrive à suivre pour les vecteurs qui semblent appartenir au plan en classique ou RR alors qu'en fait ils ne sont liés qu'à un point : direction + valeur d'une échelle abstraite par rapport au plan.
Ensuite, ça devient plus difficile. Le "transport parallèle" et les "produits vectoriels entre 4-impulsion et 4-vitesse" c'est abstrait... peut être que ça correspond à ce que je fais géométriquement mais ça ne me parle pas. C'est un blocage personnel, pas une critique de ton explication, chacun piochera dans ce qui lui parle le plus

(...) à moins de considérer que la distance à laquelle l'objet passe est arbitrairement petite pour pouvoir négliger l'écart et on en revient donc à un croisement, avec un Doppler égale au transverse en l'évènement de croisement, et au longitudinal immédiatement avant et après le croisement

Avec toutes les réserves que tu émets ok... Tant que chacun sait ce qu'il est en train de faire ça me va.
Je suis de l'avis de Zef, cette question est presque hors sujet car elle concerne la RR, oublions ça.

..........

1/ 0,268 = 3,735
Ok pour moi

J'avais vu... mais ce chiffre ne correspond pas à un shift car l'effet n'est pas réciproque.
L'observateur éloigné voit le voyageur en r avec un redshift z+1 = 2,544 x 1,468 = 3,735
mais le voyageur ne voit pas l'infini avec un blueshift 1/3,735=0,268 mais un (?)shift = 2,544 / 1,468 = 1,732 en l'occurrence rouge (soit un Doppler classique 1+B)
Seule la RG a un effet inverse, la RR reste réciproque.

[Mailou75]

Re,

Waouu t'es chaud en ce moment !

(signe à choisir selon entrant ou sortant)

Ok, c'est l'Effet Shapiro. Vu depuis l'infini, la lumière semble aller localement en r à c'=c / (z+1)² radialement, dans les deux sens (orthoradialement elle semble aller à c''=c / (z+1)

Au passage, une petite intégration nous donne

J'ai un doute... la formule que j'utilise pour les rayons lumineux en Schw est :



J'ai l'impression qu'il te manque le dénominateur Rs dans la valeur abs et la valeur absolue devrait être placée comme dans ma formule pour décrire la géodésique complète jusqu'à la singularité (c'est la condition pour que la formule continue de marcher à l'intérieur pour r < Rs). On peut même ajouter +/- devant la formule pour traiter les géodésiques entrantes/sortantes, c'est le sens de ta valeur absolue sur le t. Un peu hors sujet ici puisque qu'on se limite à l'extérieur, c'est plus pour le dénominateur que je soulève le problème.

Ce qui est bien ce qu'on attendait!

Ok, le rapport des shift reçus et aussi celui des (z+1)_r locaux. Je suis bien incapable de suivre ton calcul mais GG
J'arrive à comprendre de loin ce que tu fais mais je ne peux pas suive vraiment le détail, dommage pour moi.

On peut ensuite passer au cas le plus général, où les deux observateurs sont en mouvement quelconque...

Euh... c'est peut être pas une priorité. S'attaquer à la formule d'une géodésique lumière non radiale me semble être une étape préliminaire pour achever les cas classiques.
Par suite une chute libre non radiale éventuellement mais le cas général avec des "accélérations" en cours de chute me semble trop complexe et pas forcément didactique...
En tout cas je suis sec sur le premier point alors qu'il est particulièrement bloquant

Merci pour ton aide

Mailou

[mach3]

les "produits vectoriels entre 4-impulsion et 4-vitesse" c'est abstrait...*

Attention, ce sont des produits scalaires, pas des produits vectoriels qui n'ont rien à voir avec. La difficulté est-elle avec le produit scalaire en général, ou avec le produit scalaire entre 4-vitesse et 4-impulsion?

La suite plus tard

m@ch3

[Mailou75]

Salut,

Attention, ce sont des produits scalaires, pas des produits vectoriels qui n'ont rien à voir avec. La difficulté est-elle avec le produit scalaire en général, ou avec le produit scalaire entre 4-vitesse et 4-impulsion?

Ah... je ne fais pas bien la différence non. S'il n'y a avait que ça je ferais l'effort d'aller chercher comme je le fais quand je peux.
Non, la difficulté porte surtout sur les notations , , etc, je ne sais même pas ce qu'elles désignent alors je décroche rapidement.

Comme tu le dis, si je prends le temps d'ouvrir un bouquin et de me plonger là dedans, à ce moment là je m'autoriserais à poser des questions sur ce que je ne comprends pas. Tes calculs sont loin d'être inutiles car ils serviront à ceux qui peuvent les lire et iront en profondeur, contrairement à moi qui flotterai éternellement... Y'a trop de boulot et l'idée n'est pas de refaire mon éducation. L'essentiel pour moi c'est qu'on soit d'accord sur le résultat

[mach3]

J'ai un doute... la formule que j'utilise pour les rayons lumineux en Schw est :

C'est la même que moi à ln(2M) près. Les deux sont correctes, c'est défini à une constante additive près.

Euh... c'est peut être pas une priorité. S'attaquer à la formule d'une géodésique lumière non radiale me semble être une étape préliminaire pour achever les cas classiques.
Par suite une chute libre non radiale éventuellement mais le cas général avec des "accélérations" en cours de chute me semble trop complexe et pas forcément didactique...*
En tout cas je suis sec sur le premier point alors qu'il est particulièrement bloquant*

J'ai dit quelconque, mais je voulais dire radiaux quelconques (en particulier des chutes libres) et sur la même radiale.
La geodesique nulle non radiale est sur ma liste. Il semble que ce soit une autre paire de manches à résoudre.

m@ch3

[Mailou75]

Re,

C'est la même que moi à ln(2M) près. Les deux sont correctes, c'est défini à une constante additive près.

Ok, c’etait au cas où t’avais des bugs en l’utilisant. Je me doutais qu’il y avait une constante qq part... je conserve toujours une formule d’origine en cas de problème d’unité.

J'ai dit quelconque, mais je voulais dire radiaux quelconques (en particulier des chutes libres) et sur la même radiale.

Tu me rassures
Normalement ça ne devrait pas être compliqué en suivant la même logique : le shift (vu, tout combiné) d’un observateur statique sera multiplié par le shift (RR) d’un observateur en mouvement au même point pour savoir ce qu’il voit.

La geodesique nulle non radiale est sur ma liste. Il semble que ce soit une autre paire de manches à résoudre.

Oui j’en ai peur. D’autant que les références pour savoir si le resultat est juste vont manquer cruellement. C’est dans un tel contexte que je n’aurais aucune confiance dans mes propres calculs, par exemple...

....

Là j’essaye de traduire graphiquement le fait que z+1=(1+B)Y² est toujours vrai pour l’observateur en Rmax, même si Rmax=infini. Je galère...

A + merci

[mach3]

Ah... je ne fais pas bien la différence non.

Le produit vectoriel donne un vecteur, et c'est réservé à R³ (c'est une construction spécifique à partir de quelque chose de plus général en n dimensions, le produit extérieur). Hors sujet ici.
Le produit scalaire donne un scalaire, un nombre quoi. Et c'est vraiment pas un concept compliqué à la base, c'est niveau 1ere ou terminale si on reste dans de la géométrie euclidienne avec des coordonnées cartésiennes. Après ça ne se complique pas tant que ça, ça reste une somme de produits.

Tes calculs sont loin d'être inutiles car ils serviront à ceux qui peuvent les lire et iront en profondeur, contrairement à moi qui flotterai éternellement... Y'a trop de boulot et l'idée n'est pas de refaire mon éducation.

Le produit scalaire, et d'une manière général la métrique, car c'est de cela qu'il s'agit, est essentielle, tu gagnerais beaucoup à étudier un peu ça tout en perdant peu de temps.

m@ch3

[Mailou75]

Re,

Le produit vectoriel donne un vecteur, et c'est réservé à R³ (c'est une construction spécifique à partir de quelque chose de plus général en n dimensions, le produit extérieur). Hors sujet ici.
Le produit scalaire donne un scalaire, un nombre quoi. Et c'est vraiment pas un concept compliqué à la base, c'est niveau 1ere ou terminale si on reste dans de la géométrie euclidienne avec des coordonnées cartésiennes. Après ça ne se complique pas tant que ça, ça reste une somme de produits.

D'après ce que tu en dis j'imagine que l'un est une addition de vecteurs et l'autre une multiplication des normes par le sin de l'angle (le truc qui donne le moment cinétique). Je me trompe sans doute, je vais aller voir... mais peu importe, comme je le disais ce n'est pas le lieu pour refaire mon éducation (je parle du fil pas du forum en général lol)

.......

Là j’essaye de traduire graphiquement le fait que z+1=(1+B)Y² est toujours vrai pour l’observateur en Rmax, même si Rmax=infini. Je galère...

En fait je crois que c'est tout bête compte tenu du principe, c'est comme en classique :
Il y a entre Rmax et r une différence d'énergie "potentielle" (z+1)r/(z+1)max=E
Lorsque qu'un voyageur part de Rmax en chute libre, il arrive en r avec une énergie "cinétique" E=Y transformée en vitesse (le B lié à ce Y).
L'observateur resté en Rmax voit tout ce qui se passe en r dilaté dans le temps de ce même Y, il voit donc le voyageur avec un redshift (1+B)Y * Y, soit [Doppler local] * [dilatation/potentiel entre Rmax et r]
Quand Rmax=infini, (z+1)max=1 et E=(z+1)r=Y qui donne B et par suite un redshift vu de (1+B)Y², aussi !

[Zefram Cochrane]

Bonjour,

il s'agit de la vitesse coordonnée de la lumière à la coordonnnée r

L'intégration de R' à R donne :

pour obtenir la distance radar entre R et R' pour un observateur situé en R il faut faire :


La distance radar entre R et R' pour un observateur situé en R' est-elle : ?????

?????????

J'avais vu... mais ce chiffre ne correspond pas à un shift car l'effet n'est pas réciproque.
L'observateur éloigné voit le voyageur en r avec un redshift z+1 = 2,544 x 1,468 = 3,735
mais le voyageur ne voit pas l'infini avec un blueshift 1/3,735=0,268 mais un (?)shift = 2,544 / 1,468 = 1,732 en l'occurrence rouge (soit un Doppler classique 1+B)
Seule la RG a un effet inverse, la RR reste réciproque.

Entièrement d'accord avec ce calcul!

Avec toutes les réserves que tu émets ok... Tant que chacun sait ce qu'il est en train de faire ça me va.
Je suis de l'avis de Zef, cette question est presque hors sujet car elle concerne la RR, oublions ça.

Je ne crois pas avoir affirmé cela parce que je pense tout le contraire .
Si un mobile chute à la vitesse U lorsqu'il se trouve en R et un autre chute à la vitesse W lorsqu'il se trouve en R'
tous deux on une vitesse relative
si un observateur chute à la vitesse W lorsqu'il se trouve en R' et voit un autre à la coordonnée R chuter à la vitesse U, il le verra avec un schift :
si les deux chuteurs s'éloignent l'un de l'autre à V;
si les deux chuteurs s'approchent l'un de l'autre à V.
si un observateur chute à la vitesse U lorsqu'il se trouve en R et voit un autre à la coordonnée R' chuter à la vitesse W, il le verra avec un schift :
si les deux chuteurs s'éloignent l'un de l'autre à V;
si les deux chuteurs s'approchent l'un de l'autre à V.
La RR à toute sa place.

[mach3]

L'intégration de R' à R donne :

pour obtenir la distance radar entre R et R' pour un observateur situé en R il faut faire :


La distance radar entre R et R' pour un observateur situé en R' est-elle : ?????

?????????

ça mériterait une vérification plus approfondie, mais c'est peut être hors-sujet la distance radar non?

Avec toutes les réserves que tu émets ok... Tant que chacun sait ce qu'il est en train de faire ça me va.
Je suis de l'avis de Zef, cette question est presque hors sujet car elle concerne la RR, oublions ça.

Je ne crois pas avoir affirmé cela parce que je pense tout le contraire .
Si un mobile chute à la vitesse U lorsqu'il se trouve en R et un autre chute à la vitesse W lorsqu'il se trouve en R'
tous deux on une vitesse relative
si un observateur chute à la vitesse W lorsqu'il se trouve en R' et voit un autre à la coordonnée R chuter à la vitesse U, il le verra avec un schift :
si les deux chuteurs s'éloignent l'un de l'autre à V;
si les deux chuteurs s'approchent l'un de l'autre à V.
si un observateur chute à la vitesse U lorsqu'il se trouve en R et voit un autre à la coordonnée R' chuter à la vitesse W, il le verra avec un schift :
si les deux chuteurs s'éloignent l'un de l'autre à V;
si les deux chuteurs s'approchent l'un de l'autre à V.
La RR à toute sa place.

Vous avez tord tous les deux. La question ne concerne pas que la RR et la RR n'a pas toute sa place, on est dans un problème de RG (en tout cas on travaille dans une solution de la RG). Le fait que des choses connues dans la RR apparaissent ici ou là est par contre naturel, merci au principe d'équivalence...

Je posterais une synthèse pour le cas deux observateurs en mouvement radiaux quelconques sur la même radiale, ce sera mieux que ce bricolage branlant.

m@ch3

[Zefram Cochrane]

ça mériterait une vérification plus approfondie, mais c'est peut être hors-sujet la distance radar non?

Je suis d'accord sur le HS , mais comme l'effet Shapiro et la formule qui lui conduit a été mentionnée plusieurs fois, je tenais à préciser ce à quoi aboutissait l'effet Shapiro: calculer la distance radar.
pour ce qui est de la vérification cela pourrait se faire en temps utile sur un autre fil.

revenons donc à nos moutons :

Vous avez tord tous les deux. La question ne concerne pas que la RR et la RR n'a pas toute sa place, on est dans un problème de RG (en tout cas on travaille dans une solution de la RG). Le fait que des choses connues dans la RR apparaissent ici ou là est par contre naturel, merci au principe d'équivalence...

Je n'ai jamais dis cela , je dis seulement que la RG n'exclue pas la RR amha, mais l'intègre.

Je posterais une synthèse pour le cas deux observateurs en mouvement radiaux quelconques sur la même radiale, ce sera mieux que ce bricolage branlant.

m@ch3

Je pense que normalement, tu devrais aboutir au final avec le même résultat. Il sera quand même très intéressant de décortiquer ta synthèse et le reste pour nous familiariser avec la méthode...

[Mailou75]

Salut,

ça mériterait une vérification plus approfondie, mais c'est peut être hors-sujet la distance radar non ?

Grave...

Je posterais une synthèse pour le cas deux observateurs en mouvement radiaux quelconques sur la même radiale, ce sera mieux que ce bricolage branlant.

Je ne crois pas que ce soit un «bricolage branlant», simplement il part du resultat (simplifié dans le cas radial) : Shift perçu à distance = Doppler relativiste local * decalage gravitationnel entre observateurs. Y’a sans doute une boulette a cause du cacul de «V», je regarderai ce soir...

[Zefram Cochrane]

Correction des carrés sur les beta

Je ne crois pas avoir affirmé cela parce que je pense tout le contraire .
Si un mobile chute à la vitesse U lorsqu'il se trouve en R et un autre chute à la vitesse W lorsqu'il se trouve en R'
tous deux on une vitesse relative
si un observateur chute à la vitesse W lorsqu'il se trouve en R' et voit un autre à la coordonnée R chuter à la vitesse U, il le verra avec un schift :
si les deux chuteurs s'éloignent l'un de l'autre à V;
si les deux chuteurs s'approchent l'un de l'autre à V.
si un observateur chute à la vitesse U lorsqu'il se trouve en R et voit un autre à la coordonnée R' chuter à la vitesse W, il le verra avec un schift :
si les deux chuteurs s'éloignent l'un de l'autre à V;
si les deux chuteurs s'approchent l'un de l'autre à V.

[Mailou75]

Rapidement sur le calcul de Zef:
- Il y a une erreur sur la formule du Doppler, les B ne sont pas au carré
- Toujours sur le Doppler, il y a une inversion entre red (le + en haut) et blueshift (le - en haut)
- Pour le décalage gravitationnel on ne sait pas si R>R’ ou l’inverse mais ça ne génère pas d’erreur je pense. Simplement on ne sait pas intuitivement si le shift sera red ou blue.

Un petite application numérique aurait mis en évidence ces erreurs... hein

Par contre, si le résultat est juste, affirmer que, sans être au même évènement les voyageurs ont une «vitesse relative» me semble un raccourci dangereux. Ca marche parce qu’on peut multiplier les Doppler respectifs entre voyageurs et immobiles avant de multiplier par le décalage gravitationnel entre immobiles. A nouveau, l’essentiel est de savoir ce qu’on est en train de faire...

A +

[invite6c093f92]

J'ai parcouru très rapidement le fil, et ai encore eu une fois la même impression, je prends ça pour exemple:

Je n'ai jamais dis cela , je dis seulement que la RG n'exclue pas la RR amha, mais l'intègre.

Alors, mon impression (mais je peux me tromper) c'est que vous voulez faire de la RG avec de la RR, comme si un référentiel inertiel tangent en RG est un truc "fixe", alors qu'il est "variable", non constant quoi...( Transport//, ect...). Le fait d'avoir un potentiel gravitationnel(non-nul) implique de changer d'outils (sinon ça va être dur d'avoir une application numérique correcte).
Désolé si HS, Mach3 effacera, mais c'est ce qui me vient en tête quand je lis vos différents threads...

[mach3]

Par contre, si le résultat est juste, affirmer que, sans être au même évènement les voyageurs ont une «vitesse relative» me semble un raccourci dangereux.

voilà, c'est pour ça que je parle de bricolage (même si dans ce cas particulier ça pourrait donner un résultat correct, je n'ai pas vérifié encore...)

m@ch3

[Mailou75]

voilà, c'est pour ça que je parle de bricolage (même si dans ce cas particulier ça pourrait donner un résultat correct, je n'ai pas vérifié encore...)

Ca marche parce que multiplier des shifts ou additionner des vitesses c’est kif kif. Du coup considérer que l’un va à U et l’autre à W ou que l’un va à V=«U+W» (addition relativiste) et l’autre est immobile c’est pareil. Pas pour la description car cette vitesse n’a pas vraiment de sens mais pour le resultat.

[Mailou75]

Salut,

Alors, mon impression (mais je peux me tromper) c'est que vous voulez faire de la RG avec de la RR (...)

Non, tu te trompes. On fait de la RR localement mais de la RG (ou du moins du Schw) entre les localités. Il apparait que la RR ne change pas et que la RG est une «homothétie» décrivant comment sont vues les autres localités : compressées radialement + ralenties en dessous de toi et étirées radialement + accélérées au dessus. Cette simplification du cas radial est une voie vers la compréhension (ou pas) mais ne prétend pas expliquer le fond. Pour ça il faut partir des bases comme le fait mach3, ce n’est pas donné à tout le monde...

[invite6c093f92]

. On fait de la RR localement mais de la RG (ou du moins du Schw) entre les localités.

Comment? (désolé, tjrs pas lu le fil comme il faut, mais ce que j'ai lu ne m'apporte pas de réponse en rapport au cours que je suis...).

Il apparait que la RR ne change pas et que la RG est une «homothétie» décrivant comment sont vues les autres localités

Le point qui me "gêne" c'est que les espaces tangents étants différents...D'ou le transport//, mais comme celui-ci dépend du chemin suivit (c'est le coté "non constant" de mon précédent post), alors j'ai le défaut de pas avoir lu vos trucs (méa culpa), juste en diagonale, mais rien vu qui correspondrait à ce principe, suis encore une buse dans le domaine, mais je pense que j'aurai remarqué, maintenant, si tu veux me poiter où c'est...Merci.

En bref, (je ne sais plus si c'est à toi ou à Zef que j'ai déjà fait la remarque), j'ai tjrs cette impression que vous faites de la RR "de proche en proche", ou du moins de trouver un moyen de rentrer dans la RG de cette façon, pour prendre un exemple, si tu veux (avec votre méthode) déterminer l'énergie d'une particule "au loin", tu fais le produit scalaire de la 4-vitesse et la 4-impulsion (de la particule of course), alors c'est cool en RR mais en RG, vu que les tangents ne sont pas identiques, c'est la daube, du coup, faut faire le transport//( qui, déjà dit, dépend du chemin).

Ceci dit, c'était juste un avis en passant ,Mach3 a bien les choses en main donc autant oublier mes posts (que Mach3 peut virer si il le juge nécessaire, faut pas hésiter!).

[Mailou75]

Salut,

Voilà un petit résumé des "étapes" qui mènent graphiquement de Newton à Schwarzschild. Au départ j'ai fait une version "juste" mais elle n'a pas vraiment d'intérêt sinon que tout est approximatif et ce n'est pas forcément clair. J'ai opté pour une version graphiquement juste avec des "vitesses moyennes" mais qui traduit parfaitement ce qui est juste de façon infinitésimale. L'intervalle de temps est 0,1Rs/c (soit 1 seconde si Rs=3.000.000km).

1) En haut à droite on a Newton, la formule dr/dT.

2) Juste en dessous la "correction" dont il est question dans ce fil. La valeur locale en Rmax d'un intervalle dr est (z+1)max*dr, j'avoue que c'est léger comme argument mais j'ai pas mieux... on voit que la vitesse à l'approche de Rs tend vers c (45°) cette fois.

3) La RR nous dit que si un voyageur va à une vitesse V locale pendant une durée propre de 1s il franchira une distance beaucoup plus grande. L'axe d'espace devient une longueur propre d. Le T* signifie qu'en tout point de l'axe d'espace d des axes de temps locaux auront la même valeur "propre" pour tous les immobiles.

4) L'observateur à l'infini voit les intervalles dr d'une longueur apparente dr. En changeant de repère les rectangles colorés conservent la même surface, c'est une règle déjà en RR, toute surface est conservée par changement de repère.

5) On aboute les tronçons de trajectoire obtenus dans un repère (r;t), c'est Schw ! (Zoom 1/2)

Je ne dis pas que c'est très orthodoxe mais ça fonctionne. L'idée était de montrer que le Redshift perçu par un observateur resté en Rmax est toujours z+1=(1+B)Y². Là on comprends que si on part de la bonne vitesse locale (Fig2) il y a simplement un double effet Y par rapport à un Doppler classique : le premier est lié à la RR (passage Fig3) et le second à la RG (passage à la Fig4) puisque pour conserver sa surface en retrouvant une valeur dr d'espace, un rectangle doit s'étirer en hauteur du facteur inverse.

A suivre...

[Mailou75]

Erratum sur Rmax, merci à la modération de bien vouloir faire l'échange

##C'est fait, il a fallu que je bricole, mais j'ai réussi. Par contre je ne sais pas si je peux supprimer le message 54, si ça se trouve ça va supprimer la pièce jointe... mach3, pour la modération##

[Mailou75]

Re boulet... dsl

[Mailou75]

Annulé ... suis fatigué je crois

[Mailou75]

Bon...

J'ai enfin trouvé la relation que je cherchais dans la "simplification" dont je parlais en début de fil. Je ne sais pas si c'en est vraiment une... mais elle vaut le coup d'être exposée. Attention c'est très ésotérique, moi même je ne comprends pas tout... Je vais donc principalement exposer la construction.

Il s'agit d'une combinaison entre la parabole de Flamm dont la formule est z=2.rac[Rs(r-Rs)] et une RR locale trigonométrique (les relations entre B, Y etc sont lues sur un cercle). Comme on peut le voir tout à droite, la particularité de la parabole de Flamm est de donner une longueur propre d'espace Δd (pas forcément infinitésimale) en fonction de Δr.

En partie haute j'ai représenté les trajectoires de chute en coordonnées de Newton. Ca n'a pas vraiment d'importance, c'est juste pour visualiser de quelle chute on est en train de parler et donner un intervalle de temps propre de long de l'axe r. Rouge tombe depuis l'infini et compte 5 secondes (si Rs=300.000km) entre 4,16Rs et Rs. Bleu est en chute libre depuis Rmax=3,60Rs, il compte 10s avant d'atteindre Rs.

En bas à gauche, entrons dans le vif... Chute libre depuis l'infini : Si on suppose un vecteur déplacement tangent à l'espace en r de "norme" 1 (cad qu'on lit les valeurs de vitesse sur un cercle de rayon 1) alors la vitesse lue en r correspond bien à une vitesse de chute depuis l'infini. A la base la vitesse se lit plutôt entre le vecteur et une horizontale, mais ça revient au même. Par exemple à T=3s (je n'ai pas noté les valeurs de r pour ne pas compliquer , vous pouvez les évaluer avec l'échelle en dessous) Rouge a une vitesse v=0,630c soit 1/Y=0,776. En dessous on voit la courbe du 1/z+1 dite "trou noir" (en violet) où on retrouve la valeur de 1/Y (puisque (z+1)r=Y pour une chute depuis l'infini).

En bas à droite c'est une chute depuis Rmax, Bleu. C'est un poil plus complexe, la fameuse construction analytico-géométrique, qui n'est pas vraiment utile puisque le résultat sera géométrique. Pour connaître sur quel cercle doit être lue la vitesse il faut : partir d'un cercle de r=0,630 (pure coïncidence avec tout à l'heure...) qui revient à calculer la formule de Newton dr/dT puis dilater ce cercle de (z+1)max=1,177 ce qui revient à faire la "correction". Le cercle obtenu vaut r=0,741, ça veut simplement dire qu'à ce point la vitesse de chute depuis Rmax vaut 0,741 fois la vitesse de chute depuis l'infini (Vlib) soit v=0,503c.

On comprend pourquoi Rouge a un r=1, quelle que soit la courbe elle vaudra 1 à l'infini. J'ai noté l'équivalent de 1/Y pour Rouge (cote verticale) mais je n'ai pas encore cherché le sens. J'ai mis les valeurs si qqun veut se pencher sur le sujet, lol.

Bon jusque là j'ai juste appliqué les formules en fait... mais le truc qui fait le lien c'est que si on prend un axe de "temps" perpendiculaire à l'espace local alors, pour un intervalle 1s de temps propre c'est bien un intervalle d'espace dr qui est parcouru, dans tous les cas de figure (aux imprécisions près visibles dues au fait que 1s c'est pas infinitésimal...).

......

Et là, j'en perds le nord ! J'avoue que je ne sais plus dans quel sens doit se regarder la figure...où est l'espace, où est le temps ? Pourquoi la "ligne d'univers" (intervalle T=1s) est elle orthogonale à l'espace et pas colinéaire à lui ? L'inclinaison progressive du vecteur vitesse jusqu'à 90° par rapport à l'infini explique t elle l'horizon (vitesse relative c en RR trigo) ? Ou est passé l'intérieur puisque la parabole de Flamm admet un +/- devant la formule donc une symétrie verticale (j'ai représenté la suite de la courbe verte...). WTF ?

Bref, c'est pas mûr parce que je n'y comprends rien mais c'est juste mathématiquement. Je ne pensais pas en parler ici mais plutôt en discussions libres, finalement il est tellement lié à ce qui est déjà dit sur ce fil que ce serait compliqué de tout répéter. Je vous le livre sans grande justification mais c'est bientôt les vacances et j'aurais plus d'ordi, snif. Ca donnera le temps d'y réfléchir... j'ai envie d'imaginer que les rayons des cercles sont des histoires d'énergie, c'est pas clair...


Merci pour vos réactions

Mailou

[mach3]

Synthèse

Note : on utilise les coordonnées de Schwarzschild restreintes au cas radial, (t,r), la signature étant (+-). on pose c=G=1.


plus familièrement écrite


1) relation entre coordonnées de la 4-vitesse et vitesse coordonnée
On considère la ligne d'univers d'un objet. En un évènement de coordonnée (t,r) de cette ligne d'univers sa vitesse coordonnée est . Un 4-vecteur u de coordonnées en cet évènement est tangent à la ligne d'univers de l'objet. Son carré scalaire vaut :


La 4-vitesse de l'objet, de coordonnées est elle aussi tangente à la ligne d'univers, elle est donc colinéaire u, c'est à dire qu'on U=ku, et , d'où , soit plus proprement, et

au 4-vecteur précédent, mais son carré scalaire doit valoir 1, c'est à dire que :


On a donc


Les coordonnées de la 4-vitesse sont donc (oui, c'est pas très beau, mais j'ai pas trouvé plus joli pour l'instant...)

2) relation entre 4-vitesse d'un observateur, 4-impulsion d'une particule et énergie
Soit un observateur de 4-vitesse U, coordonnées , et une particule de 4-impulsion P, coordonnées se croisant en un évènement donné. L'énergie de la particule mesuré par l'observateur est :


3) 4-impulsion et vitesse coordonnée d'une particule de genre nul
Si la particule est de genre nul (par exemple un photon), alors le carré scalaire de sa 4-impulsion, tangente à sa ligne d'univers, doit être nul, on a :



Le vecteur p, de coordonnées , avec la vitesse coordonnée de la particule de genre nul, est lui-aussi tangent à la ligne d'univers (il est colinéaire à P) et est donc aussi de genre nul :




4) Transport parallèle de la 4-impulsion d'une particule de genre nul en chute libre
La géodésique de la particule en chute libre est une courbe de paramètre (chaque évènement ayant des coordonnées ) tel que l'équation des géodésiques est satisfaite :


Un vecteur de coordonnées étant tangent à la géodésique.
Cette équation des géodésiques impose que ce vecteur, transporté dans sa propre direction le long de la géodésique, ne doit pas changer (ses coordonnées, oui, mais pas le vecteur lui-même) : il est transporté parallèlement. C'est notamment ce qu'on attend de la 4-impulsion qui doit se conserver localement. Ce vecteur de coordonnées est donc identifiable à la 4-impulsion de la particule de genre nul, à une constante multiplicative près (qu'on peut prendre égale à 1 si on choisit convenablement).

La résolution de la deuxième équation donne la contrainte suivante sur : (pour le détail, se reporter au message 31)
Cela impose la forme suivante pour les coordonnées de la 4-impulsion P : avec a une constante.

Bilan :
Considérons :
-un observateur émetteur, situé en en l'évènement d'émission, ayant une vitesse coordonnée et de 4-vitesse , dont les coordonnées sont : (oui, c'est toujours pas très beau)
-un observateur récepteur, situé en en l'évènement de réception, ayant une vitesse coordonnée et de 4-vitesse , dont les coordonnées sont : (oh, c'est bon, ça suffit maintenant)
-un photon allant de l'émetteur au récepteur, de 4-impulsion P, dont les coordonnées sont : (r valant à l'émission et à la réception)

Energie du photon pour l'émetteur :






Autre version qui sera surement utile :


Energie du photon pour le récepteur (même calcul, avec à la place de ) :

Autre version qui sera surement utile :


Rapport des énergies récepteur/émetteur (ou des fréquences, ou inverse des longueurs d'ondes):


Autre version qui sera surement utile :



Plus qu'à remplacer les vitesses coordonnées par ce qu'on veut...

Annexe : vitesse de l'émetteur et du récepteur par rapport à des immobiles de Schwarzschild qu'ils croisent au moment de l'émission et de la réception respectivement, donc en et

Un immobile de Schwarzschild en r, a pour 4-vitesse U_0, de coordonnées (U^t_0,0). On a :

Donc

Le facteur , témoignant de la vitesse relative entre un observateur en mouvement, de 4-vitesse U, et cet immobile de Schwarzschild en l'évènement où ils se croisent, est donné par :



On a (non, pas de commentaires, même en annexe, vous commencez à être lourd à la fin!)

Donc



La vitesse relative entre un observateur en mouvement et cet immobile de Schwarzschild en l'évènement où ils se croisent, est donc :
(au signe près, qui dépend de la convention choisie : vitesse relative positive si l'observateur en mouvement monte ou descend).

Le rapport d'énergie du photon entre récepteur et émetteur peut donc se réécrire en fonction des vitesses de l'émetteur et du récepteur relatives à des immobiles de Schwarzschild qu'ils croisent aux évènements d'émission et de réception, respectivement :



Je ne suis pas convaincu de l'utilité de cette dernière formule, mais vu que cela semble vous tenir à coeur, je vous la donne donc en cadeau.

Note de fin : ce post contient surement des coquilles et mérite une relecture approfondie, il se peut que des corrections y soit apportées ultérieurement. Ne pas hésiter à signaler une erreur.

m@ch3

[mach3]

Salut,

Voilà un petit résumé des "étapes" qui mènent graphiquement de Newton à Schwarzschild. Au départ j'ai fait une version "juste" mais elle n'a pas vraiment d'intérêt sinon que tout est approximatif et ce n'est pas forcément clair. J'ai opté pour une version graphiquement juste avec des "vitesses moyennes" mais qui traduit parfaitement ce qui est juste de façon infinitésimale. L'intervalle de temps est 0,1Rs/c (soit 1 seconde si Rs=3.000.000km).

[...]

En fait ce que tu essaies de faire semble analogue à vouloir couvrir une bande de la surface terrestre avec des cartes raboutées les unes aux autres, avec en plus la contrainte que les cartes de départ ne sont pas conformes (angles non respectés, il faut corriger leur aspect ratio) et que la représentation d'arrivée n'est pas conforme non plus (par exemple une bête représentation latitude longitude orthonormée).

On commence par corriger les cartes de départ afin que la géométrie Euclidienne s'y applique en bonne approximation et on ajuste leurs échelles pour qu'elles soient cohérentes. Ensuite on les colles bout à bout, puis on déforme le tout pour que ça rentre dans la représentation.

Tu sembles faire la même chose, tu corriges les cartes de départ afin que la géométrie de Minkowski s'y applique en bonne approximation (ce que tu appelles faire de la RR localement), tu ajustes les échelles, tu les colles bout à bout, puis tu déformes le tout pour que ça rentre dans la représentation en coordonnées de Schwarzschild.

Au lieu de dire que tu fais de la RR localement, il faut dire que la géométrie de Minkowski est une bonne approximation localement (une fois qu'on a corrigé correctement les cartes). En fait ça c'est toujours faisable. Il y a toujours un système de coordonnées où, en un événement donné (et même, éventuellement, sur toute une ligne), la métrique a les mêmes coefficients que celle de Minkowski en coordonnées de Lorentz, et la géométrie de Minkowski s'applique donc aux vecteurs attachés en cet événement, et elle s'applique de manière approximative au voisinage de l'événement.

m@ch3

[Mailou75]

Salut et merci pour l'intérêt que tu portes à ma question

##C'est fait, il a fallu que je bricole, mais j'ai réussi.

Thx, il était tard j'ai enchainé les c... dsl

Synthèse

Cette fois j'arrive à suivre les maths qui sont de mon niveau, les explications sont nickel. On voit que c'est des combinaisons de dr/dt et de (z+1)r et ça me va bien...

J'ai seulement une petite remarque... par exemple quand tu dis "Si la particule est de genre nul (par exemple un photon), alors le carré scalaire de sa 4-impulsion, tangente à sa ligne d'univers, doit être nul" j'aimerais bien comprendre quel est le sens du carré scalaire d'une 4-impulsion, pourquoi il est intéressant de l'étudier et pourquoi vaut il zero ? Je chipote t'en fais déjà des masses... mais une petite explication de principe (sans pour autant rentrer dans des maths que justement je ne comprendrais pas) juste pour ne pas perdre le fil

Rapport des énergies récepteur/émetteur (ou des fréquences, ou inverse des longueurs d'ondes):

J'ai regardé ces formules, j'y met un petit bémol en tant que formules "généralistes" : Si R1 et en dessous de R2 et que Beta positif désigne une vitesse vers le haut alors ces formules fonctionnent, partiellement. Elles donnent la variation de fréquence perçue par l'observateur en R2 (quels que soient les signes de B1 et B2). L'inverse mathématique E1/E2 donne l'allongement des longueurs d'onde pas ce que voit celui en R1, il faut une deuxième formule :



NB : Je trouve donc cette notation "E2/E1" extrêmement dangereuse.

Tu sembles faire la même chose, tu corriges les cartes de départ afin que la géométrie de Minkowski s'y applique en bonne approximation (ce que tu appelles faire de la RR localement), tu ajustes les échelles, tu les colles bout à bout, puis tu déformes le tout pour que ça rentre dans la représentation en coordonnées de Schwarzschild.

Oui mais tu as l'air de dire que je fais ma tambouille... Le Scwh est un vrai, la longueur de d est vraiment la longueur propre de Flamm et approximer une "vitesse moyenne" sur l'intervalle est moins faux que d'appliquer la vitesse à un angle au carré entier puisqu'au final je n'ai même pas eu à tricher sur les rectangles du Schw. De toute façon dessiner l'infinitésimal ce sera toujours faux, le dessin porte sur une logique qu'il est plus facile de comprendre en "sublimant" la réalité. Je ne triche jamais d'habitude.

Au lieu de dire que tu fais de la RR localement, il faut dire que la géométrie de Minkowski est une bonne approximation localement

La nuance est trop subtile pour moi

Merci

Mailou

[mach3]

Cette fois j'arrive à suivre les maths qui sont de mon niveau, les explications sont nickel.

Pas l'impression qu'elles soient plus simples que dans les messages précédents. Le texte les explique peut-être mieux. Ou alors tu fais des progrès.

J'ai seulement une petite remarque... par exemple quand tu dis*"Si la particule est de genre nul (par exemple un photon), alors le carré scalaire de sa 4-impulsion, tangente à sa ligne d'univers, doit être nul"*j'aimerais bien comprendre quel est le sens du carré scalaire d'une 4-impulsion, pourquoi il est intéressant de l'étudier et pourquoi vaut il zero ? Je chipote t'en fais déjà des masses...

Des masses ? Tu ne crois pas si bien dire. Le carré scalaire de la 4-impulsion est la masse au carré ! Cela suffit-il ou alors il y a besoin d'un développement ?

J'ai regardé ces formules, j'y met un petit bémol en tant que formules "généralistes" : Si R1 et en dessous de R2 et que Beta positif désigne une vitesse vers le haut alors ces formules fonctionnent, partiellement. Elles donnent la variation de fréquence perçue par l'observateur en R2 (quels que soient les signes de B1 et B2). L'inverse mathématique E1/E2 donne l'allongement des longueurs d'onde*pas ce que voit celui en R1, il faut une deuxième formule

Bien vu, au point 4, j'ai imposé sans faire attention un photon entrant en prenant P^r positif (parce que a est positif). Pour le cas sortant il faudrait que P^r=-a (P^t demeurant inchangé ). Du coup il y a un signe qui va se ballader. Il faut que je vérifie et que j'ammende mon bilan.

Oui mais tu as l'air de dire que je fais ma tambouille... Le Scwh est un vrai, la longueur de d est vraiment la longueur propre de Flamm et approximer une "vitesse moyenne" sur l'intervalle est moins faux que d'appliquer la vitesse à un angle au carré entier puisqu'au final je n'ai même pas eu à tricher sur les rectangles du Schw. De toute façon dessiner l'infinitésimal ce sera toujours faux, le dessin porte sur une logique qu'il est plus facile de comprendre en "sublimant" la réalité. Je ne triche jamais d'habitude.*

Le problème est qu'il n'est pas sûr que telles méthodes soient efficaces en dehors du cas radial, notamment si ce qui est derrière est mal compris.

La nuance est trop subtile pour moi*

En y réfléchissant, cela mériterait un fil, et/ou une discussion en privé avec une connaissance commune qui ne vient plus sur le forum. La question n'est peut-être pas si simple. "A t'on le droit de dire qu'en espace temps courbe on peut faire de la RR localement ?" C'est limite philo. On a envie de dire "vous avez 4h".

m@ch3