Bonjour à tous,
Je suis passionnée d'astrophysique et je me pose quelques questions concernant les trous noirs, mais je précise que je ne maîtrise pas (et de loin) tous les outils mathématiques pour les décrire.
Premier point : la forme de l'horizon.
Pour un trou noir de Schwarzschild, c'est simple, l'horizon est sphérique et on a :
Pour un trou noir de Kerr (c.a.d. en rotation), on a cette formule :
On voit clairement que ce rayon ne dépend pas de la latitude, donc un trou noir de Kerr devrait être parfaitement sphérique.
Le soucis c'est que de nombreux sites représentant un trou noir en rotation montrent un ellipsoïde.
Quelques exemples : Wikipedia ; Wikipedia anglais ; Astrosurf
J'aimerais donc savoir où se situe la vérité.
Deuxième point : la singularité.
Pour un trou noir de Schwarzschild c'est un point : OK
Pour un trou noir de Kerr, c'est un anneau, ce serait dû à la force centrifuge.
Le problème c'est que sous la sphère des photons (r = 1,5Rs) la force centrifuge s'inverse et pointe vers le centre du trou noir, je ne vois donc pas pourquoi la singularité prendrait la forme d'un anneau...
Et si on applique le même raisonnement à l'horizon, il devrait rester le même aux pôles, et rétrécir à l'équateur, ce qui n'est manifestement pas le cas.
Troisième point : l'ergosphère.
Son rayon est :où θ représente la latitude.
À l'équateur on adonc
et au pôle
donc
et ainsi
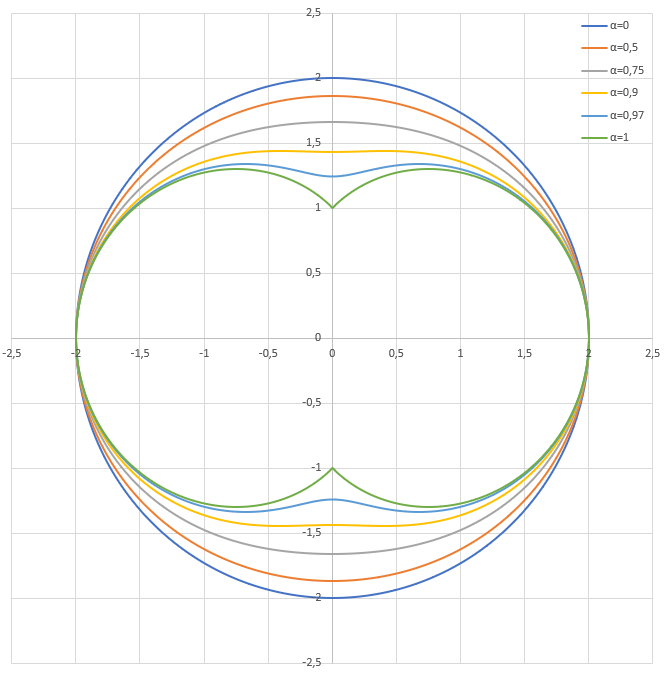
La courbe définie par R en faisant varier θ est :
en posant
(α=0 pour un trou noir de Schwarzschild et α=1 pour un trou noir extrémal).
J'ai tracé les courbes correspondantes pour α=0 ; α=0,5 ; α=0,75 ; α=0,9 ; α=0,97 ; α=1 et à ma grande surprise l'ergosphère n'est pas un ellipsoïde de révolution mais devient une sorte de citrouille quand α se rapproche de 1.
Est-ce exact ? Wikipédia montre un ellipsoïde en version française (ainsi que de nombreux sites et ouvrages) et une sorte de citrouille en version anglaise.
Quatrième point qui ne concerne pas vraiment la forme des trous noirs mais qui m'intrigue c'est la courbure de l'espace. J'ai souvent lu que l'horizon des événements Rs (Schwarzschild) n'est pas vraiment une sphère de rayon Rs car ce rayon n'est pas mesurable directement mais une sphère de circonférence C = 2∙pi∙Rs ce qui me paraît bizarre car la courbure de l'espace devrait imposer que C / Rs soit différent de 2Pi.
Vos explications sont donc les bienvenues
Et enfin le dernier point : la vitesse de libération et la vitesse orbitale (pour une orbite circulaire).
Pour simplifier on traitera le cas d'un trou noir de Schwarzschild.
Voici les formules "classiques" :
- vitesse d'évasion :
- vitesse orbitale :
Ces formules restent elles valables au voisinage d'un trou noir ?
- pour la vitesse d'évasion c'est cohérent car pouron a
=> la formule est correcte sur l'horizon mais le reste elle très près d'un trou noir ?
- pour la vitesse orbitale ça ne va pas car sur la sphère des photons on adonc
=> ce qui est faux car les photons étant en orbite autour du trou noir on devrait avoir!
Voici donc ma question : quelle est la formule qui donne la vitesse orbitale Vo autour d'un trou noir en fonction de r et de M ?
Conclusion : pas mal de chose étant un peu contre-intuitives (mais bon, l'intuition avec les trous noirs et la relativité c'est un peu spécial), merci d'éclairer ma lanterne

-----