bonjour
il semble qu'il soit possible de calculer ce rayon à partir de Oméga Lamda, 1-Oméga Lambda, H0, et z redshit pour un univers plat
H0 constante de Hubble
Lambda : constante cosmologique
Oméga : paramètres de densité respectifs
Merci si vous pouvez m'aider
Bien cordialement
-----




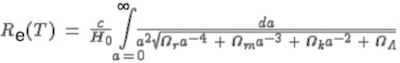



 ) seule pour ce calcul. d'où l'intérêt plus que limité du rayon de Hubble dans l'histoire.
) seule pour ce calcul. d'où l'intérêt plus que limité du rayon de Hubble dans l'histoire.