Exercice : Comment construire l'espace-temps de façon euclidienne ?

[externo]

Bonjour,

Expliquons pourquoi l’espace-temps plat est supposé avoir une métrique de Minkowski et non d’Euclide.
Prenons une fusée se déplaçant à vitesse constante X/T.
X et T sont exprimés en secondes.
γ est le facteur de contraction de Lorentz.
Les transformations de Lorentz impliquent que l’espace de la fusée est contracté et son temps dilaté (en fait contracté lui aussi)
Vu de l’extérieur, la fusée fait un trajet de X secondes dans l’espace et T secondes dans le temps.
Mais vu de l’intérieur de la fusée, le trajet n’est que X/γ secondes dans l’espace et T/γ secondes dans le temps.

Pour que l’espace-temps soit euclidien il faudrait que la distance spatio-temporelle soit conservée par changement de repère.
Mais ici, nous avons une distance au carré de X²+T² dans le repère extérieur à la fusée et (X²+T²)/γ² dans le repère intérieur.
Il n’y a donc pas conservation de la distance euclidienne par changement de repère.

Curieusement, la valeur conservée, au lieu d’être X²+T² est X²-T²
C’est comme si au lieu de s’ajouter euclidiennement à la longueur temporelle, la distance parcourue dans l’espace s’en soustrayait.

Quel ajustement mathématique faudrait-il pour rendre euclidienne la métrique ?
Imaginons que la contraction des longueurs ait pour origine une rotation euclidienne de l’espace-temps sur le passage de la fusée.
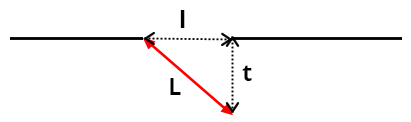
En basculant, l’espace de la fusée se trouve comme sur un plan incliné ayant pour longueur la longueur L de la fusée, par conséquent L s’écrit dans le repère immobile extérieur L²=l²+t².
Le l, c’est l’espace contracté, le t, c’est la non synchronisation des horloges le long du plan incliné. L’espace de la fusée est partiellement orienté dans le passé de l’espace-temps extérieur dans le sens de son mouvement.



De cette façon, la fusée franchit une distance de longueur X/γ non seulement dans son propre repère mais dans le repère extérieur. Le même raisonnement est applicable à l’axe du temps. Dans les deux repères le carré de l’intervalle euclidien peut donc s’écrire (X²+T²)/γ², il est donc invariant par changement de repère.

L’existence réelle de cette rotation rendrait l’espace-temps euclidien. Or, il n’aura pas échappé que cet espace incliné ressemble à l’espace contracté d’un champ gravitationnel. Et il se trouve qu'il existe bien un champ gravitationnel qui grandit avec γ : celui induit par l’énergie cinétique...
-----

[Nicophil]

Bonjour,

De cette façon, la fusée franchit une distance de longueur X/γ non seulement dans son propre repère mais dans le repère extérieur.

Qui est immobile dans le repère extérieur ?

[externo]

On peut imaginer que la fusée se déplace entre deux planètes immobiles l'une par rapport à l'autre, mais elle peut très bien le faire loin de toute matière. Il suffit que la fusée évolue dans un espace plat qui possède une certaine orientation figurée ici horizontale.

[pm42]

On peut imaginer que la fusée se déplace entre deux planètes immobiles l'une par rapport à l'autre

Ca veut dire quoi 2 planètes immobiles l'une par rapport à l'autre ? Si elles sont seules, elles s'attirent. Si l'une est en orbite autour de l'autre, il faut préciser un référentiel de préférence inertiel et elles ne sont pas immobiles.

Il suffit que la fusée évolue dans un espace plat qui possède une certaine orientation figurée ici horizontale.

Ce quoi "l'orientation" d'un espace plat ?

[A voir en vidéo sur Futura]

[externo]

Ca veut dire quoi 2 planètes immobiles l'une par rapport à l'autre ? Si elles sont seules, elles s'attirent. Si l'une est en orbite autour de l'autre, il faut préciser un référentiel de préférence inertiel et elles ne sont pas immobiles.
Ce quoi "l'orientation" d'un espace plat ?

On suppose que les planètes sont suffisamment éloignées pour négliger leur interaction réciproque.
Si on figure l'axe du temps vertical, l'axe d'espace est une droite horizontale donc l'espace est plat. Si on fait un changement de repère par rotation, l'orientation des axes change mais l'espace reste une droite donc plat.

[mach3]

On ferme. Point 6 de la charte.

mach3, pour la modération