théorie des groupes et astronomie

[pachacamac]

L'une des origines de l'idée de groupe est l'étude des équations algébriques par Joseph-Louis Lagrange (1771). La terminologie de « groupe » est mise en évidence pour la première fois par Évariste Galois (1830) source wikipedia
-----

[Deedee81]

Salut,

Un peu d'humour dans ce monde de brute et pour passer un bon week-end
https://home.deds.nl/~dvdm/dirk/Phys...FourGroup.html

[JPL]

Bizarre : MalwareBytes me bloque ce lien avec le motif : serait susceptible de contenir une action malveillante.

[Deedee81]

Bizarre : MalwareBytes me bloque ce lien avec le motif : serait susceptible de contenir une action malveillante.

Ah ennuyant ça. Pourtant chez moi c'est assez sévère et ce n'est pas bloqué. Tu préfère qu'on sucre ? De toute façon, ce n'est que de l'humour.

[JPL]

Laisse le lien. MBAM est très sévère et bien que ce soit un programme réputé, je pense que dans sa surveillance en temps réel des sites web il indique un certain nombre de faux positifs.

[pachacamac]

Afin que tu puisse aussi profiter de l'humour de ce lien voici vers quoi il renvoie

[physeb2]

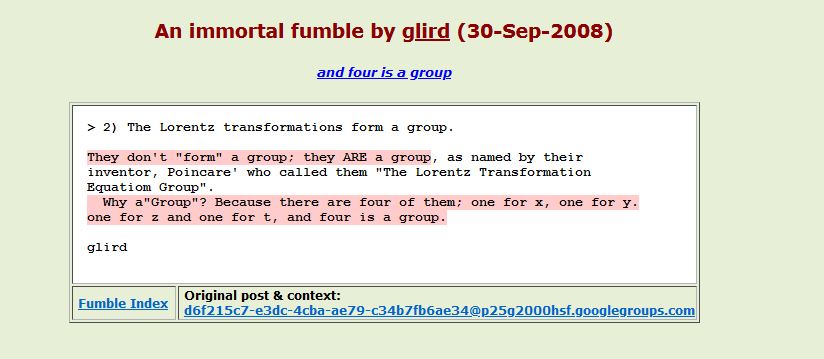
Bonjour Pachacamac,

c'est un sujet un peu technique donc je ne rentrerai pas dans les détails.

L'idée est que tu as les équations d'Einsteins, qui permettent de décrire la relation entre la géométrie d'une zone que tu considère (donc la zone sur laquelle tu applique les équations) et son contenue en énergie et impulsion.
Tu peux, sous certaines hypothèse de simplifications, obtenir une solution analytique dans pour un fluide homogène. Ces solutions sont les équations de Friedmann et permettent d'estimer l'évoltuion de l'Univers moyen (background Universe en anglais, c'est ainsi que tu le remcontrera plus fréquemment)

Maintenant, l'Uivers n'est pas homogène a toutes les échelles. Il ne l'est pas pour les zones de rayon inférieur a 100 Mpc/h, heureusement sinon on ne serait pas là pour en discuter. Afin de décrire ces inhomogénéités, le plus courrant en physique est d'appliquer un traitement perturbatif.
C'est à dire, prendre tes équations de bases et perturber chaque quantité présente dans les équations. Par exemple la densité :

où le terme en delta est la perturbation locale a la position x et au temps t. Tes équations vont devenirs gigantesques et tu vas gentiement virer tout les termes que tu peux sous des considérations de "dans ces conditions, ce terme est négligeable".

Maintenant, la particularité des Equations d'Einstein, c'est qu'il y a aussi une métrique (la partie liée à la géométrie) et elle aussi se perturbe! Le théorème de décomposition des perturbations donne une base de décomposition de celles-ci (Scalaire- Vecteur - Tenseur) . Ce genre de chose vient de la décomposition en représentations irréductibles du groupe de symétrie associé à la métrique. Il y a qussi des histoires de jauge dans ce cas, mais je ne suis pas spécialiste donc je préfère ne pas en parler, seulement préciser que les calculs de ces perturbations se fait de manière commune dans le Jauge dite de Newton.

Ensuite tu fais les calculs pour estimer l'évoltion de toutes ces perturbations, et c'est pas chose aisée. Mais c'est exactement ce que tu fais pour prédire les perturbations à la fin de l'inflation puis dans le CMB (les perturbations scalaires sont associées en premier lieu avec la temperature et de polarisation E, celles tensorielles avec les modes B de polarization).
Dans le modèle standard de la cosmologie, il n'y a pas de perturbations vectorielles primordiales. Mais certains autres modèles si, c;est par exemple le cas de la version relativiste de MOND : qui s'aeppele TeVeS. le nom veut dire "Tensor Vectorial Scalar"....

J'espère que c'était compréhensible, je suis incapable de faire moins technique pour parler de ce sujet.

[pachacamac]

Muchas gracias Seb,

C'est limpide. j'ai tout compris.

Hasta pronto.

[pachacamac]

Un beau document pour mieux comprendre certains groupes : Introduction aux groupes de Lie pour la physique (et aux groupe de Lorentz et Poincaré

[pachacamac]

le groupe de symétrie associé à la métrique

Je serai curieux de savoir de quel groupe il s'agit...
En lien avec le tenseur métrique gmunu ?

Merci

[physeb2]

Bonjour Pacahcamac,

Serait t'il possible nous expliquer un peu ce que dit le "théorème de décomposition des perturbations"

Je ne suis certainement pas le plus désigné pour expliquer cela. Il y a une vidéo de Scienci Egregia qui explique pas mal de ces choses là:
https://youtu.be/TNxd5_51siA

Surtout la première heure. Il ne rentrera pas dans les cas que j'ai mentionné, mais il y a les groupes de symétries (des groupes cinématiques) et la décompisition en représentation irréductibles.

J'espère que ça t'apportera les compléments que tu recherche.