Je suis persuadé que nos désaccords viennent d' une erreur de notation.
0,9| n' est pas un nombre fixe, mais la limite d' une suite.
De même que r(n) est une suite.
Quand on écrit l' infini en utilisant comme symbole un "8" allongé, croyez vous que l' on a fixé ce nombre ?
non !
C' est juste une manière d' écrire pour indiqué quelque chose, mais c' est approximatif et non pas parfaitement exact.
Exemple :
1/3 est un nombre fixe
mais 0,3| est la limite d' une suite
donc pour être rigoureux 1/3 n' est pas égal à 0,3|
Ecrire que 1/3=0,3| est un abus de langage, une commodité
Pareil pour 0,9|=1
LeLama, dans ta démonstration qui dit que la distance qui sépare 0,9| de 1, est nulle, tu te trompes.
Elle n' est pas nulle, elle tend vers zéro, c' est la limite d' une suite, ce n' est pas un nombre fixe. Pour preuve, essaies de trouver plus petit que la limite de f(x)=1/x quand x tend vers l' infini et cette limite de f(x) on peut toujours l' intercaler entre 0,9| et 1.
Autre question, j' ai entendu dire que des mathématiciens travaillaient sur cette proposition :
" il n' y a pas assez d' entiers naturels pour remplir l' ensemble N"
En avez vous entendu parler ?
-----





 dans
dans  )
)


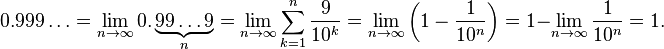
 je trouve juste qu'on tourne en rond... le probleme quand tu dis "La limite d' une suite convergente semble être un nombre fixe, mais non c' est un nombre indéterminable malgré tout.", c'est d'une part que c'est mal defini (que veux dire indeterminable), d'autre part non justifié (c'est une impression que tu as, mais il faut le prouver). en un mot ca n'est pas des maths.
je trouve juste qu'on tourne en rond... le probleme quand tu dis "La limite d' une suite convergente semble être un nombre fixe, mais non c' est un nombre indéterminable malgré tout.", c'est d'une part que c'est mal defini (que veux dire indeterminable), d'autre part non justifié (c'est une impression que tu as, mais il faut le prouver). en un mot ca n'est pas des maths.