Bonjour,
j'ai à faire pour vendredi un Dm sur les fonctions et les vecteurs...je suis perdu je n'y comprends plus rien



Pourriez-vous m'aider
Voici deux exercices de mon DM que je n'arrive vraiment pas à réaliser :
Exercice 1 :
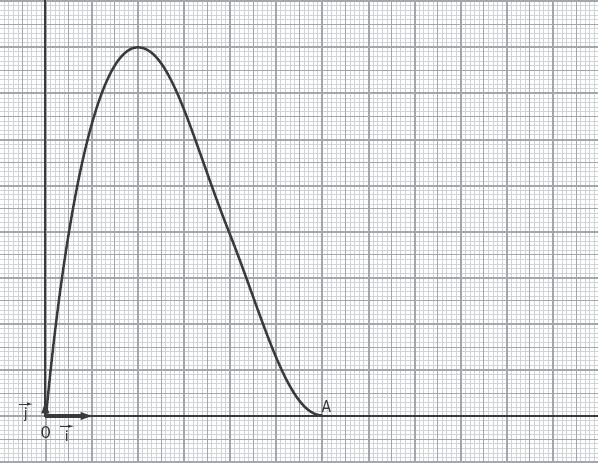
On considère la courbe C que vous trouverez en cliquant sur le lien suivant :
Cette courbe a pour équation y = x(6-x)2 sur l'intervalle [0, 6] dans le repère (O, , ).
On considère le point A (6,0).
Soit M un point de [OA] d'abscisse x; et M' son symétrique par rapport à A.
1) exprimer x' l'abscisse de M' en fonction de x :
Je trouve x' = x +2 racine carré de (6-x)²...est-exacte ?
2) Déterminer les équations des 3 courbe C1, C2 et C3 obtenues à partir de C respectivement par symétrie par rapport à:
- la droite d'équation x = 6
-l'axe des abscisses
-le point A
Je ne sais vraiment pas coment faire...Tout ce que j'ai compris c'est que :
_ la courbe de C1 est symétrique à la courbe de C par rapport à la droite passant par A parralèle à l'axe des ordonnées...Mais comment déterminer son équation ?
_ la fonction représentée par la courbe C3 est une fonction impaire.
Comment faire pour déterminer l'équation de ces 3 courbes ?
______________________________ _________________
Exercice 2 :
On considère dans un repère orthonormé (O,,) le point A(3,2) et M(x,0) où x est un réel supérieur à 3? La droite AM coupe l'axe des ordonnées en N.
1) On me demande de calculer l'orrdonnée de N...Je sais habituellement résoudre ce type de question mais ne connaissant pas x (x>3) je ne sais pas comment faire, je sais seulement faire cela avec par exemple x = 4 :
soit 1 point M (x', y) du plan. le vecteur AB a pour coordonnées : (4-3, 0-2) et le vecteur AM' : (x'-3 ; y-2) ; M(x', y) appartient à (AM) si et seulement si il existe un nombre réel K tel que vecteur AM' = K fois vecteur AM ; c'est à dire si :
x-3 = K et y-2 = -2k soit si x = K+3 et y = -2K + 2
Le point N appartient à (AM)(Oy) donc il existe un réel K tel que :
x = 0
y = -2K+2
x = K+3 on trouve finalement que K = -3 d'où y (ordonnée de N) = 8...voilà ce que je trouve avec x = 4 comment faire avec x > 3 ???
En attente de votre aide
!
MERCII !!!
Très Cordialement.
-----