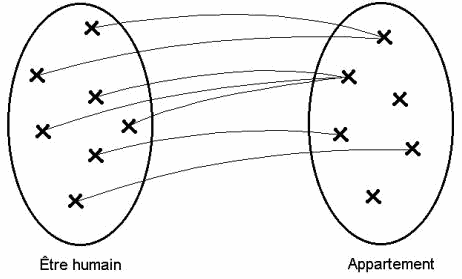
Bonjour!
Je passe en MPSI et en lisant un peu le cours de MPSI il y a quelque chose que je n'ai pas compris:
on a n un entier naturel non nul, un ensemble En={m entier nat, 1 (inf. ou =) m (inf. ou =) n}, et une application f de En dans lui-même.
Alors f est bijective equiv. f est injective equiv. f est subjective.
Ce que je ne comprends pas, c'est l'équivalence des trois affirmations.
Quelqu'un peut m'expliquer?
A 15ans tu passe en MPSI , waouh ? est-ce que tu dispose de la démo déja ?
Salut,
pour ma part, je sors de PCSI, mais je pense pouvoir t'aider (au moins sur ce point) :
cette triple équivalence est toujours vraie.
C'est à mettre en relation avec les définitions de bijection, injection et surjection.
Surjection, c'est quand tu prend un élément de l'ensemble d'arrivée Fn, et tu constate que plusieurs élements de l'ensemble de départ E1, E2, ..., Ek, si on leur applique la fonction f, donnent Fn (dans l'ensemble d'arrivée).
donc tu as AU MOINS 1 antécédent de Fn par f. on dira que f est surjective.
Injection, c'est quand tu prend un élément de l'ensemble d'arrivée Fn, et tu constate que tu as un élément E1 (ou aucun élément) de l'ensemble de départ qui te donne Fn par f.
donc tu as AU PLUS 1 antécédent de Fn par f. on dira que f est injective.
Si ces 2 conditions sont équivalentes. C'est à dire, si pour un élément de l'ensemble d'arrivée de f, tu as en même temps au plus un antécédent et au moins un antécédent, cela signifie que la fonction f a toujours 1 seul antécédent dans l'ensemble de départ.
On dira que f est bijective.
donc tu comprend maintenant l'équivalence...
Dans ton cas, En=Fn (donc la bijection associe à un élément d'un ensemble, un élément dans la même ensemble)
puisque c'est précisé "dans lui-même"...
et ta précision 1<m<n signifie juste que les indices de En et Fn sont supérieurs ou égaux à 1...
le pricipal pour comprendre l'ensemble du raisonnement, est la définition même de bij, inj et surj...
l'important, ethiop, c'est que ici, En est un ensemble fini.
Ca se voit bien en faisant des dessins, mais je te ferai une esquisse de démonstration après.
voila pour le schéma, c'est vrai que ca aide à comprendre...
(être humain représente En, et appartement représente En également)
les fléches entre chaque élément de départ et d'arrivée représentent f (qui à 1 élément de départ associe 1 élément d'arrivée)
après, tu peux constater sur le schéma si f est bijective, surjective ou injective.
Donc, des éléments de démo :
Déjà, on peu généraliser un peu :
soit f une application de E dans F, avec card(E)=card(F) et E et F ensembles finis.
L'équivalence repose sur le fait que dans ces conditions, on a :
-f injective <==> card(f(E))=card(E)
-f surjective <==> card(f(E)=card(F)
Il reste uniquement à signaler que card(E)=card(F) pour pouvoir conclure.
On peut maintenant se demander un peu d'où viennent ces égalités :
Il faut déjà bien voir (ça se prouve par récurrence), que si un ensemble est inclus dans un autre, alors, le cardinal du premier sera inférieur ou égal au cardinal du second.
Maintenant, montrons
-f injective <==> card(f(E))=card(E)
si f est injective, on peut construire une bijection de E dans f(E) (en effet, chaque élément de f(E) a au moins un antécédent par définition d'ensemble-image, et pas plus d'un par définition d'injectivité), d'où card(E)=card(f(E))
(ça peut aussi se montrer, par récurrence, que si on a une bijection entre deux ensembles, ils ont même cardinal)
l'autre sens de l'implication, si card(f(E))=card(E), c'est un peu plus subtil. Il faut construire une bijection d'une partie de E vers f(E). Pour ça, on prend un élément de f(E), et on lui associe un de ses antécédents dans E. L'ensemble des antécédents choisis est noté G.
Comme G est en bijection avec f(E), ils ont même cardinal. Par hypothèse, f(E) et E ont même cardinal. Ainsi, G et E ont même cardinal. Or, G est une partie de E, et s'ils sont même cardinal, ils sont donc égaux (on peut le montrer aussi...).
Ainsi, tout élément de f(E) admet un unique antécédent par f, puisque si certains éléments avaient plusieurs antécédents, E aurait un cardinal plus grand que G. donc f est injective.
Le raisonnement est similaire pour montrer que
-f surjective <==> card(f(E)=card(F)
D'où l'équivalence.
(j'espère ne pas m'être moi même embrouillé dans ces raisonnements parfois un peu délicats)
Envoyé par citron_21
Si ces 2 conditions sont équivalentes. C'est à dire, si pour un élément de l'ensemble d'arrivée de f, tu as en même temps au plus un antécédent et au moins un antécédent, cela signifie que la fonction f a toujours 1 seul antécédent dans l'ensemble de départ.
On dira que f est bijective.
donc tu comprend maintenant l'équivalence...
Cependant, tu n'expliques pas pourquoi f injective <==> f surjective, ce qui est le point dur.
Bonjour,
thorin comment définis tu le cardinal d'un ensemble fini ?
le cardinal d'un ensemble fini représente le nombre d'éléments contenus dans l'ensemble. par exemple si tu as un ensemble E={-1,5,7,18}, alors cardE=4
Certes, mais on peut le définir plus formellement.
On dit qu'un ensemble est fini s'il existe n dans N tq l'ensemble soit en bijection avec [|1,n|] (ceci étant un intervalle d'entiers = tous les entiers compris entre 1 et n)
Et une fois une telle bijection trouvée, on définit le cardinal de l'ensemble comme étant égal à n.
créer une bijection entre tous les éléments de l'ensemble et l'intervalle d'entiers [1,n] revient à compter tous les éléments, n'est-ce pas ? Je n'aurais pas pensé à le formuler de telle manière
La formulation est celle de mon cours^^
Dans ce cas j'apporte une petite précision, tu as dit : "ça peut aussi se montrer, par récurrence, que si on a une bijection entre deux ensembles, ils ont même cardinal"
Avec la définition que tu donnes il n'y a pas besion de récurrence et c'est quasiment immédiat.
Effectivement^^, c'est même complètement immédiat XD
Quand j'écrivais, j'essayais surtout de pas faire de fautes de raisonnements, d'où l'inattention^^
D'ailleurs je ne pesne pas que tu aies fait de faute de raisonnement, je trouve ta démonstration de l'équivalence intéressante. (celle que je connaissais utilisait une récurrence).
Oui, moi aussi je trouve cette démo très belle.
Il faut juste avoir l'idée de base pour chacune des 2 implications, c'est-à-dire de travailler avec les cardinaux, et de mettre en bijection les ensembles ^^
Merci pour ces réponses claires. Je n'avais effectivement pas bien compris les notions de bijection, d'injection et de surjection. Mais on est sur des ensembles finis. Qu'en est-il des ensembles non finies? Pourquoi dit-on par exemple que ln(x) réalise une bijection de R+* sur R? C'est parce-que tout élement de R possede un antécédent sur R+* et un seul car la fonction ln(x) est strictement monotone sur R+*, c'est ça?
Maintenant, est-ce qu'elle réalise pour autant une injection ou une surjection?
Les deux ensembles sont infinis, peut-on dire qu'ils ont des cardinaux égaux? Ou bien serait-ce possible qu'il y ait des ensembles infinis "plus grand" que d'autres ensembles infinis. Mon intuition me porte à opter pour la seconde proposition.Maintenant, mon intuition...
alors, les définitions restent valables, mais il n'y a pas équivalence entre être injective et être surjective.Qu'en est-il des ensembles non finies?
C'est exact.Pourquoi dit-on par exemple que ln(x) réalise une bijection de R+* sur R? C'est parce-que tout élement de R possede un antécédent sur R+* et un seul car la fonction ln(x) est strictement monotone sur R+*, c'est ça?
Une fonction qui réalise une bijection réalise aussi forcément une surjection et une injection ; on peut l'expliquer ainsi : si tout élément de l'ensemble d'arrivée a un unique antécédent, alors, on peut dire qu'il en a au moins 1, et aussi qu'il en a au maximum 1.Maintenant, est-ce qu'elle réalise pour autant une injection ou une surjection?
Ca dépend des ensembles. Par exemple, le cardinal de Q est égal au cardinal de N, mais pas au cardinal de R.Les deux ensembles sont infinis, peut-on dire qu'ils ont des cardinaux égaux?
On peut le dire comme ça. Pour reprendre mon exemple précédent, on a que R est "plus grand" que N. Mais N fait la même taille que Q, car on peut construire une bijection de N vers Q.Ou bien serait-ce possible qu'il y ait des ensembles infinis "plus grand" que d'autres ensembles infinis.
Si tu veux chercher des infos, tu peux chercher sur les ensembles "dénombrables" (comme N),, les ensembles non-dénombrables, comme R, ou encore sur la "diagonale de cantor", qui est une explication à la question "pourquoi R n'est pas dénombrable ?"
Thorin.
Merci beaucoup Thorin.
Sur ce point, j'ai déja vu quelque part la démonstration intuitive du fait que l'on puisse mettre en bijection N et Q, mais pas N et R (ou Q et R).
on écrit en colonne quelques éléments de N (0,1,2,3,4,5,6) et quelques éléments de Q (-0.3,-0.2,-0.1,0,0.1,0.2,0.3), puis on relie chacun des éléments 1 à 1 (on les met en bijection).
L'expérience montre qu'on peut tous les relier (par exemple 0 à 0, 1 à 0.1, 2 à -0.1, etc...), c'est pourquoi cardN=cardQ.
Cependant, si l'on substitue l'ensemble Q par l'ensemble R, on remarque qu'entre 2 éléments de Q mis en bijection avec 2 éléments de N, on peut trouver au moins 1 éléments de R qui ne pourra donc pas entrer en bijection avec un éléments de N (d'après la définition, bijection : 1 élément n'a qu'1 antécédent)... On dira que Q est dense dans R (entre chaque couple d'éléments de Q, on peut toujours trouver des éléments R).
C'est pourquoi cardQ=cardN, mais cardR>cardN... (même si les ensembles avec lesquels on travaille ne sont pas finis)
(je ne pense pas la démonstration très rigoureuse cependant
C'est le principe de la diagonale de Cantor, pour plus d'amples informations à ce sujet.
J'en ai entendu parler une fois, mais ce n'est pas également le nom d'une fractale "la diagonale de Cantor" ?
Quelle culture ! Tu avoueras que c'est une belle démo de la non dénombrabilité de R!
Je me souviens l'avoir lu dans l'excellent livre de Walter Rudin : Principes de l'analyse mathématique , 3edition , Dunod ( Titre anglais : Principles of mathematical analysis , McGraw Hill , 1979) surnommé baby Rudin
Que je recommande a tous
C'est archi-faux! Ce qui est vrai c'est que f bijective=> f injective et =>f surjective . et inversement : f injective et f surjective=>f bijective Donc f bijective<==>f injective , f surjective
tu te trompes weensie, dans les conditions qu'ethiop a indiquée (application d'un ensemble fini dans lui même) la double équivalence est vraie.
oui je l'ai remarqué apres pardonnez moi
Vive les prof de Terminale qui font du hors programme !
