Démonstration sur une parabole variable

[invitebfd4f968]

Bonjour, je suis en première S cette année et j'ai un dm de maths que je n'arrive pas à faire. J'ai essayé de chercher dans mon cours, dans mon livre et sur internet et j'ai demandé de l'aide à des amis mais je n'y arrive pas. Pouvez-vous m'aider.

Alors :

1) Ensemble décrit par le sommet S de la parabole variable (Pm) :
(P) est la parabole d'équation : y=2x²+mx+3 où m est un réel quelconque. Soit S son sommet. On a aussi A(1;1) et B(-1;1) sur (C).
a. Exprimer les coordonnées de S en fonction de m.
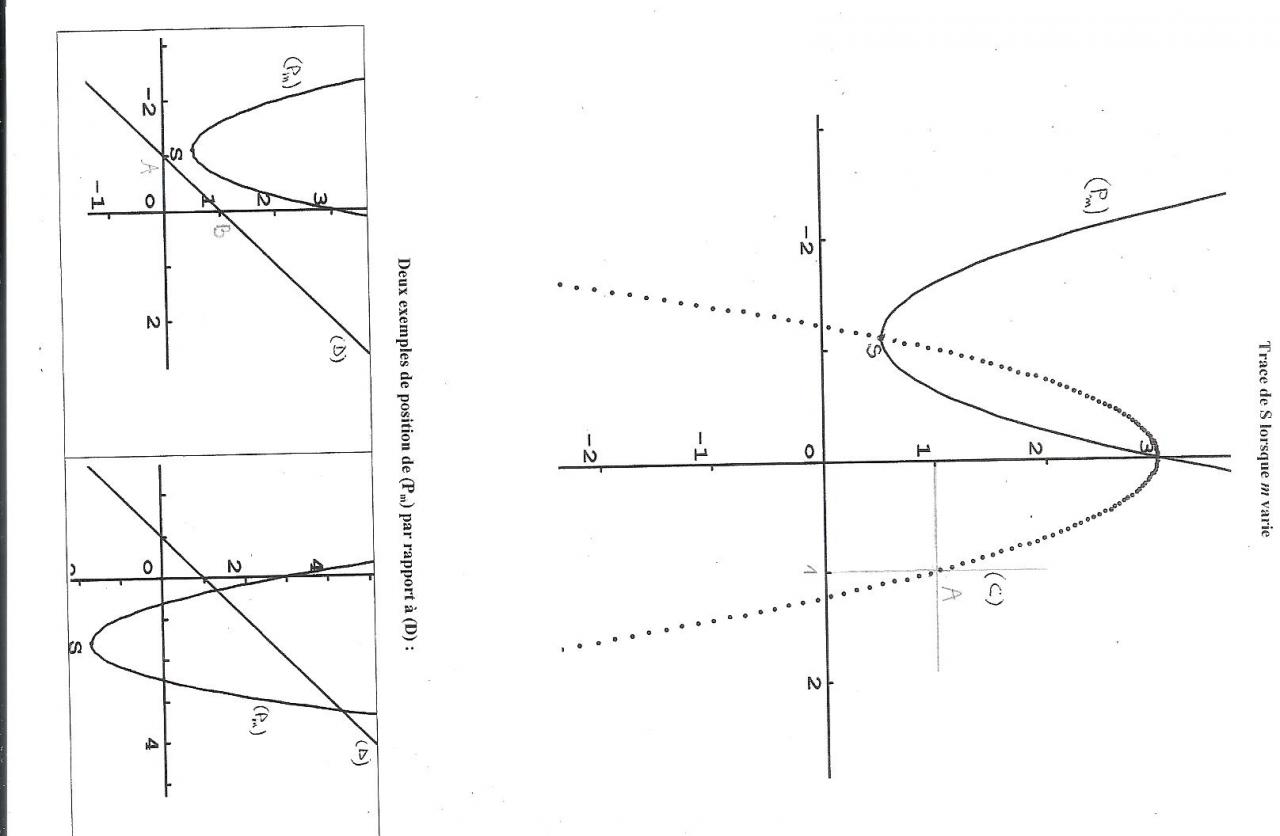
b. Déterminer à partir du graphique l'équation de la parabole (C) sur laquelle semble se trouver S.
c. Vérifier alors que S appartient bien à la courbe (C). Cela suffit-il à prouver que S décrit la courbe (C)?

2)Etude de l'intersection de (Pm) avec (D) :
(D) est la droite d'équation y=x+1
a. Ecrire l'équation que doivent vérifier les abscisses des points d'intersection de (Pm) et (D) puis mettre cette équation qous la forme ax²+bx+c=0
b. Exprimer le discriminant du trinôme obtenu en fonction de m.
c. Discuter alors suivant les valeurs de m le nombre de points d'intersection entre (Pm) et (D).

J'ai tenté pour la 1)a. : Comme les coordonnées d'un sommet sont (alpha;beta)alors alpha=-m/2a et beta=f(-m/4) ce qui me donne S(-m/4;f(-m/4)).
Pour la 1)b. : La parabole (C) a pour sommet S1(0;3) donc a(x-alpha)²+beta on a alors ici a(x-0)²+3. On a A de coordonnées (1;1) donc f(1)=1.
y= a(x-0)²+3
1= a+3
-2=a

Donc l'équation est -2(x-0)²+3.
Est-ce que c'est bon ? Pouvez-vous m'aider ? Merci d'avance.
-----

[Duke Alchemist]

Bonsoir.

1.a. Tu peux poursuivre en exprimant f(-m/4) en fonction de m.
1.b.& c. Attendons la validation de la PJ...

2.a. Les intersections de D avec P_m se détermine en égalisant les deux équations ce qui après regroupement des termes en fonction des puissances de x donne ...?... (du type ax²+bx+c=0...)
2.b.& c. Pas de difficulté normalement.

C'est tout de même un classique ce type d'exo ! A savoir maîtriser...

Cordialement,
Duke.

[invitebfd4f968]

Re

1.a. Tu peux poursuivre en exprimant f(-m/4) en fonction de m.
Mais comment exprime-t-on f(-m/4) en fonction de m ?

Je n'ai toujours pas compris.

[Duke Alchemist]

Re-

Il te suffit de remplacer x par -m/4 dans l'équation associée à f...

Duke.

[A voir en vidéo sur Futura]

[invitebfd4f968]

Ce qui nous donne y= 2m²/16 + m²/4 +3 ? Mais dans la question 1.a., on me demande les coordonnées de S en fonction de m donc (S-m/4;f(-m/4)). Quand est-ce que j'ai besoin de mentionner y=2m²/16 +m²/4 + 3 ? A la place de f(-m/4) dans mes coordonnées ?

[invitebfd4f968]

Pour 2.a. :
On égalise les deux équations c'est à dire : P(m) : y=2x²+mx+3 et (D) : y=x+1 Donc 2x²+mx+3=x+1
2x²+mx+3-x-1=0
2x²+mx-x+2=0 ??

[Duke Alchemist]

Re-

Ce qui nous donne y= 2m²/16 + m²/4 +3 ? Mais dans la question 1.a., on me demande les coordonnées de S en fonction de m donc (S-m/4;f(-m/4)). Quand est-ce que j'ai besoin de mentionner y=2m²/16 +m²/4 + 3 ? A la place de f(-m/4) dans mes coordonnées ?

f(-m/4) = 3 - m²/8 ou (24-m²)/8... (après simplification)

Pour 2.a. :
On égalise les deux équations c'est à dire : P(m) : y=2x²+mx+3 et (D) : y=x+1 Donc 2x²+mx+3=x+1
2x²+mx+3-x-1=0
2x²+mx-x+2=0 ??

En effet, l'expression que tu obtiens peut être écrite sous la forme 2x²+(m-1)x+2=0.

Tu peux exprimer le discriminant qui sera fonction de m et déduire les réponses aux questions qui suivent.

Duke.

[invitebfd4f968]

Merci pour la 2.a.

f(-m/4) = 3 - m²/8 ou (24-m²)/8... (après simplification)

Mais comment en arrive t'on là avec y=2m²/16 +m²/4+3 ?

[invitebfd4f968]

2.b. Exprimer le disciminant du trinôme obtenu en fonction de m.
2x²+(m-1)x+2=0
Delta = b²-4ac et ici, a=2; b=(m-1); c=2
Donc, Delta=(m-1)²-4*2*2
= (m-1)²-16
Est-ce que je dois laisser l'expression comme ceci ou est ce que je dois la développer pour arriver à : m²-2m-15 ??

[Duke Alchemist]

Bonjour.

... Mais comment en arrive t'on là avec y=2m²/16 +m²/4+3 ?

Peut-être parce que c'est y = 2m²/16 - m²/4 + 3 (je n'avais pas vu l'erreur )

2.b. Exprimer le disciminant du trinôme obtenu en fonction de m.
2x²+(m-1)x+2=0
Delta = b²-4ac et ici, a=2; b=(m-1); c=2
Donc, Delta=(m-1)²-4*2*2
= (m-1)²-16
Est-ce que je dois laisser l'expression comme ceci ou est ce que je dois la développer pour arriver à : m²-2m-15 ??

Il vaut mieux garder la forme factorisée pour en étudier le signe plus facilement
D'ailleurs (m-1)²-16 est encore factorisable (c'est du a²-b² donc ...).

Duke.

[invitebfd4f968]

Donc pour 1.a. : Exprimer les coordonnées de S en fonction de m :
On a S(-m/4; -m²/8+3) ?

2.b. Exprimer le dicriminant du trinôme obtenu en fonction de m.
Delta = (m-1)²-16 = (m-5)(m+3)

[invitebfd4f968]

2.c. Discuter alors suivant les valeurs de m le nombre de points d'intersection entre (Pm) et (D).
Delta = (m-5)(m+3) donc deux points d'intersection entre (Pm) et (D). Est-ce ça ?

[invitebfd4f968]

1.b. Déterminer à partir du graphique l'équation de la parabole (C) sur laquelle semble se trouver S.
La parabole (C) a pour sommet S1(0;3) donc a(x-alpha)²+beta on a alors ici a(x-0)²+3. On a A de coordonnées (1;1) donc f(1)=1.
y= a(x-0)²+3
1= a+3
-2=a
Donc l'équation est -2(x-0)²+3.
Est-ce bon ?

1.c. Vérifier alors que S appartient bien à la courbe (C). Cela suffit-il à prouver que S décrit la courbe (C) ?

[Duke Alchemist]

Re-

2.c. Discuter alors suivant les valeurs de m le nombre de points d'intersection entre (Pm) et (D).
Delta = (m-5)(m+3) donc deux points d'intersection entre (Pm) et (D). Est-ce ça ?

Le nombre d'intersection dépend du signe du discriminant et son étude est plutôt rapide.

Duke.

[invitebfd4f968]

On a donc deux intersections entre (Pm) et (D) car 2x²+(m-1)x+2=0 est positif donc intersection quand m=m-5 ou quand m=m+3 ?

1.b. Déterminer à partir du graphique l'équation de la parabole (C) sur laquelle semble se trouver S.
La parabole (C) a pour sommet S1(0;3) donc a(x-alpha)²+beta on a alors ici a(x-0)²+3. On a A de coordonnées (1;1) donc f(1)=1.
y= a(x-0)²+3
1= a+3
-2=a
Donc l'équation est -2(x-0)²+3.
Est-ce bon ?

1.c. Vérifier alors que S appartient bien à la courbe (C). Cela suffit-il à prouver que S décrit la courbe (C) ?

[Duke Alchemist]

Re-

On a donc deux intersections entre (Pm) et (D) car 2x²+(m-1)x+2=0 est positif donc intersection quand m=m-5 ou quand m=m+3 ?

Il te faut étudier le signe de (m+3)(m-5) suivant les valeurs de m

1.b. Déterminer à partir du graphique l'équation de la parabole (C) sur laquelle semble se trouver S.
La parabole (C) a pour sommet S1(0;3) donc a(x-alpha)²+beta on a alors ici a(x-0)²+3. On a A de coordonnées (1;1) donc f(1)=1.
y= a(x-0)²+3
1= a+3
-2=a
Donc l'équation est -2(x-0)²+3.
Est-ce bon ?

L'équaton de (C) paraît bonne y=-2x²+3

1.c. Vérifier alors que S appartient bien à la courbe (C). Cela suffit-il à prouver que S décrit la courbe (C) ?

Que trouves-tu en remplaçant x par l'abscisse de S, c'est-à-dire -m/4, dans l'équation trouvée ci-dessus ?

Duke.

[invitebfd4f968]

On a donc deux intersections entre (Pm) et (D) car 2x²+(m-1)x+2=0 est positif donc intersection quand m=m-5 ou quand m=m+3 ?
Il te faut étudier le signe de (m+3)(m-5) suivant les valeurs de m

Comment étudier le signe de (m+3)(m-5) suivant les valeurs de m ?
m-5=0 ou m+3=0
m=5 ou m=-3
Donc (Pm) et (D) ont deux points communs quand ]-00;-3[U]5;+00[

Que trouves-tu en remplaçant x par l'abscisse de S, c'est-à-dire -m/4, dans l'équation trouvée ci-dessus ?

:
y=-2x²+3 et S(-m/4;-m²/8+3)
-2*(-m/4)²+3
2m²/16+3

[Duke Alchemist]

Re-

Comment étudier le signe de (m+3)(m-5) suivant les valeurs de m ?
m-5=0 ou m+3=0
m=5 ou m=-3
Donc (Pm) et (D) ont deux points communs quand ]-00;-3[U]5;+00[

Il manque les cas 1 intersection et les cas pas d'intersection qui sont évidentes mais à indiquer pour répondre entièrement à la question posée.

y=-2x²+3 et S(-m/4;-m²/8+3)
-2*(-m/4)²+3
2m²/16+3

Euh... attention ! Refais bien le calcul. Il serait bien de retrouver -m²/8 + 3.

Duke.

[invitebfd4f968]

y=-2x²+3 et S(-m/4;-m²/8+3)
-2*(-m/4)²+3
2m²/16+3
Euh... attention ! Refais bien le calcul. Il serait bien de retrouver -m²/8 + 3.

2m²/16+3 = m²/8+3 non ?

[Duke Alchemist]

Re-

Non...
Le "-" devant le "2" n'a pas de raison de disparaître... (contrairement à celui du "(-m²/4)²")

Duke.

[invitebfd4f968]

Donc erreur de calcul. -2*(m/4)²+3 = -2m²/16+3=-m²/8+3