Bonsoir, je suis en seconde, j'ai besoin d'aide pour faire cet exercice s'il vous plait.
On dispose d'une feuille de carton carré, de coté 12 cm. On va construire une boite sans couvercle, de la manière suivante.
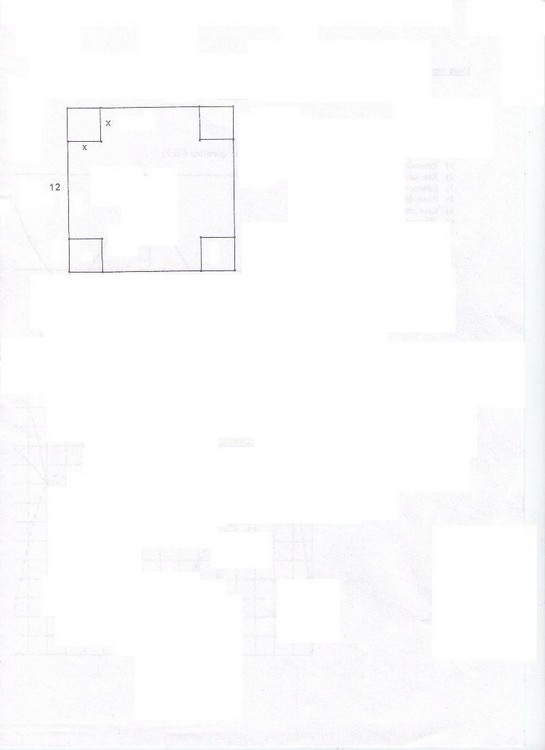
Dans chaque angle, on découpe un carré de coté x. Puis on plie suivant les pointillés pour obtenir une boite sans couvercle(voir figure).
Le but du problème est de déterminer x pour pouvoir construire une boite ayant un volume maximal.
1) On note V(x) le volume de la boite. Montrer que : V(x)=x(12-2x)²
2) Quel est l'ensemble de définition de la fonction V ?
3) Étude de la fonction à la calculatrice.
a) Rentrer la fonction V à la calculatrice.
b) Obtenir sur la calculatrice le tableau de valeurs:
x / 0 / 0.5 / 1 / 1.5 / 2 / 3 / 4/ 4.5 / 5 / 5.5 / 6
à compléter
v(x)
c) A l'aide de ce tableau de valeurs, régler la fenêtre graphique puis afficher la courbe représentative de V. Conjecturer à l'aide de la touche "trace" ou de la touche "calc" la valeur de x qui rend ce volume maximal
4) Démonstration de la conjecture faite graphiquement
a) Démontrer que V(x) - 128 = 4(x-2)²(x-8)
b) quel est le signe de x-8 ? En déduire le signe de V(x) -128
c) Conclure
Mes réponses :
1) hauteur de la boite * le fond de la boite
= x * (12-2x)²
est-ce juste ?
2) Comment répondre à la question 2 ?
Merci pour votre réponse
-----




