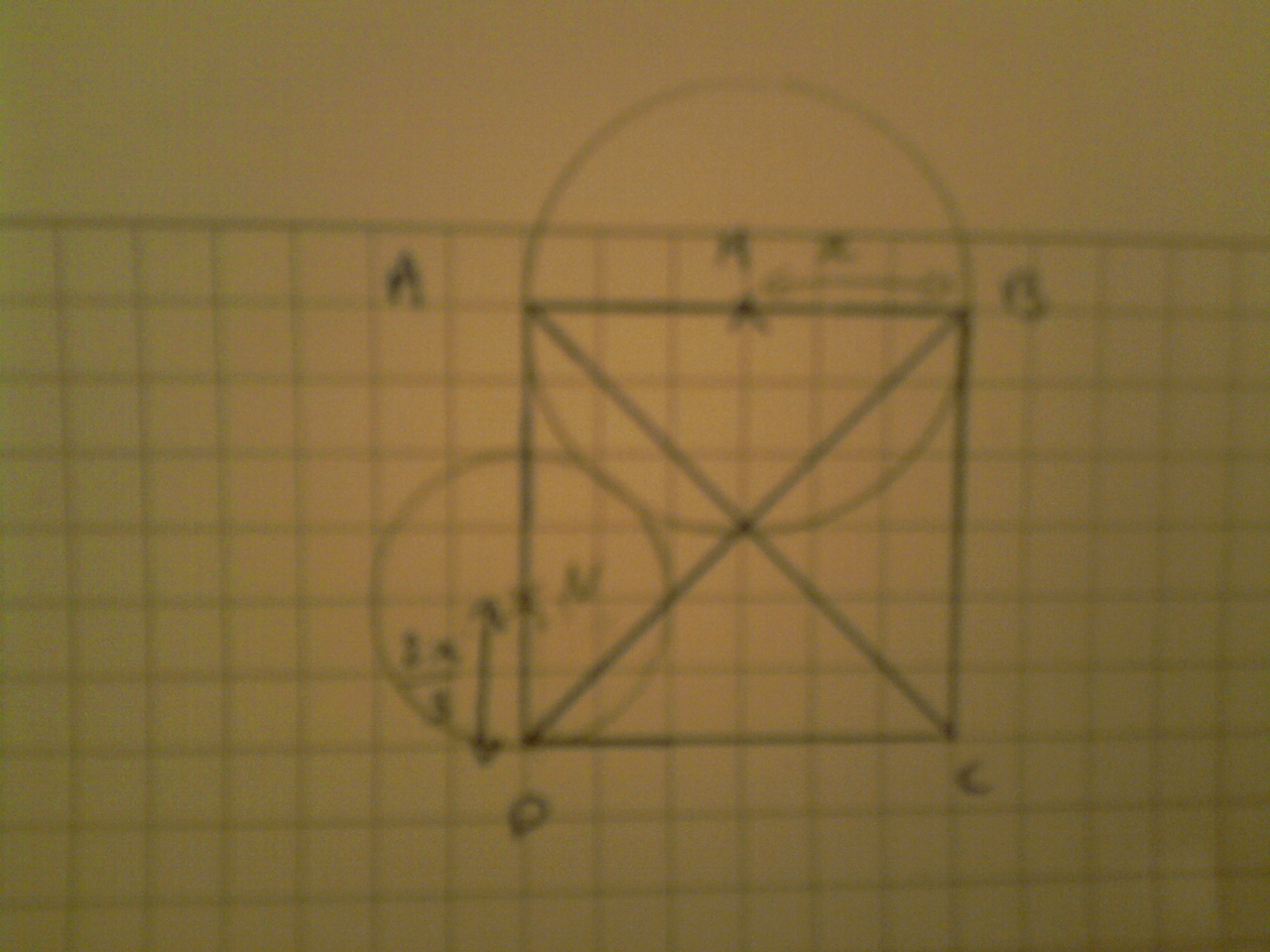Bon, l'exercice au fait, je bloque sur la 2eme question ... (et j'en ai pas fini avec les autre)
1-ABCD est un carré dont la longueur est de 2 (unité), pour tous x dans [0;2]
2-On nomme M le point faisant partie de [AB] soit BM = x
3-Dessine le point N dans [AD] soit le cercle dont le point N est le centre et passe par D est tangentiel au cercle dont le centre est le point M qui passe par B
4-On nomme la distance DN par y (Dn = y )
5-Démontre que : MN² = (2-x)² + (2-y)² (==>> ça j'ai su le faire)
Et que : MN² = (x+y)² (La j'ai vraiment bloquée quoi --' )
6-Conclus que : y = (-2x+4) / (x+2)
7-Soit f(x) = y et x est inclus dans [0;2]
>Démontre que f(x) = -2 + 8
x+2
8-Conclus les variations de la fonction f
9-Dessine Cf dans un repère orthonormé
Voila, franchement la 2eme partie de la question 5 elle m'a vraiment soulé quoi --' je l'ai trouvé dur --', le truc c'est que vu que(d'après mon raisonnement) si MN²= (2-x)²+(2-y)² et que MN² = (x+y)² donc logiquement (2-x)²+(2-y)² = (x+y)² je me trompe o_O ?? le truc c'est que je ne trouve pas le m^me resultat quand je développe --'
Merci d'avance
-----