Exercice 1ere S Maths n°99 page 127 du livre Déclic mathématique

[nahz]

Boujour j'ai un exercice que j'ai pas compris ou peut-être c'est trop dur ; Pouvez-vous m'aider SVP
C'est sur le chapitre4 Etude des variations d'une fonction. L'exercice est ci-dessous :




-----

[PlaneteF]

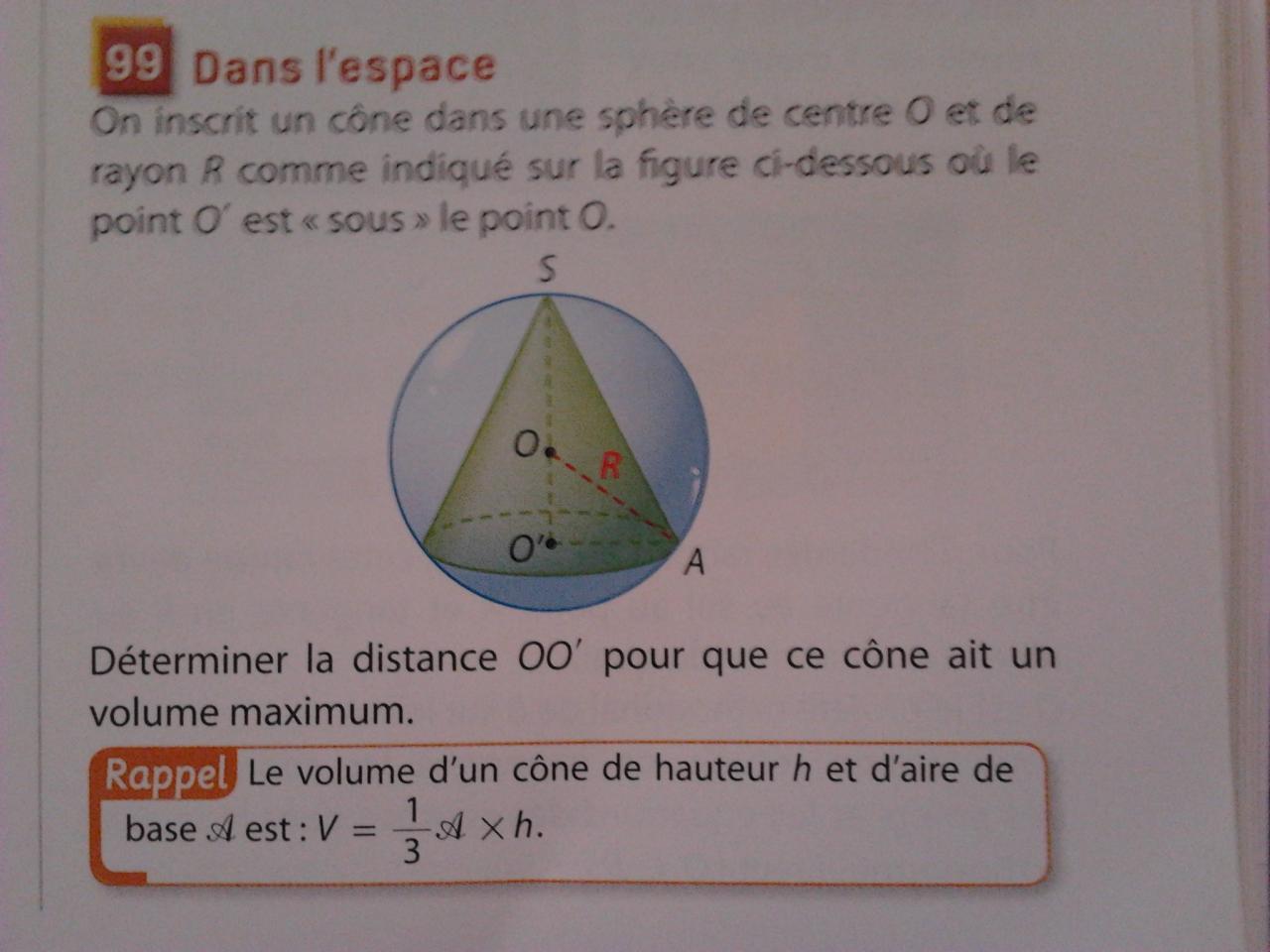
Boujour j'ai un exercice que j'ai pas compris ou peut-être c'est trop dur ; Pouvez-vous m'aider SVP
C'est sur le chapitre4 Etude des variations d'une fonction. L'exercice est ci-dessous :

Bonsoir,

Tu poses :

A partir de là, tu peux exprimer très simplement et en fonction de et .

Tu auras ainsi une expression de .

Pour connaître la valeur maximale de , tu étudies en regardant où cela s'annule, ... et c'est terminé !

[nahz]

?_? j'ai toujours pas compris pouvez-vous me détailler l'exercice SVP
je suis un peu cons c'est pour ça .

[zyket]

Avec les points du schéma comment peux-tu exprimer l'aire, A, de la base du cône ? (sachant que l'aire d'un disque c'est : ...? )

Comment exprimer sa hauteur h avec les points du schéma ?

[A voir en vidéo sur Futura]

[nahz]

Je sais pas, pouvez-vous me donner la réponse ??

[zyket]

Qu'est-ce que tu ne sais pas ? Calculer l'aire d'un disque (cherche dans wiki "aire d'un disque")? Trouver quelle distance entre deux points du schéma correspond au rayon de la base du cône (regarde bien le schéma et cherche les points qui forment un rayon de la base) ? Trouver quelle distance entre deux points du schéma correspond à la hauteur h du cône (regarde bien le schéma et cherche les points qui forment la hauteur du cône)?

Il se fait tard, je vais me coucher

[nahz]

toujours rien compris

[PlaneteF]

toujours rien compris

Commençons alors par le plus simple.

Notons comme je l'avais proposé précédemment : .

La hauteur de longueur du cône, va de quel point à quel point sur la figure ? ...

Et donc, comment exprimes-tu en fonction de et ?

La réponse est essentiellement "visuelle", ce n'est même pas des maths !

[nahz]

La hauteur c'est O'S , donc h = O'S ou h = O'O + R c'est ça ??
et ensuite comment fait-on pour l'Aire ??

[nahz]

Et pour l'aire c'est PI * R² donc V(x)= 1/3(PI * R²) * (x + R) C'est ça ??

[PlaneteF]

Et pour l'aire c'est PI * R² donc V(x)= 1/3(PI * R²) * (x + R) C'est ça ??

OK pour la hauteur, ... faux pour l'aire de la base.

Regarde bien la figure, ... le rayon de la base n'est pas mais .

Il faut donc exprimer en fonction de et , ... tout simplement en utilisant le théorème de Pythagore dans le triangle , rectangle en O'.

[nahz]

R²=x²+O'A²
O'A²=R²-x²
donc O'A=R-x c'est bon??

[nahz]

et l'Aire sera = 1/3(PI*(R-x))*(R+x) donc V(x)=1/3(PI*(R-x))*(R+x)

[PlaneteF]

O'A²=R²-x²
donc O'A=R-x c'est bon??

HORREUR !!!

Relis ce que tu viens d'écrire autant de fois nécessaires jusqu'à ce que cela te fasse dresser les cheveux sur la tête !!!

[nahz]

non je me suis trompé, c'est O'A=_/R²-x²

[PlaneteF]

non je me suis trompé, c'est O'A=_/R²-x²

En fait tu n'as pas besoin d'expliciter O'A, ce qui t'intéresse ici c'est O'A².

[danyvio]

HORREUR !!!

Relis ce que tu viens d'écrire autant de fois nécessaires jusqu'à ce que cela te fasse dresser les cheveux sur la tête !!!

Mes cheveux à moi n'ont pas pu se dresser : je suis chauve, mais ils ont quand même essayé !

[nahz]

donc c'est V(x)=1/3(PI*(_/R²-x²))*(R+x) c'est bon????

[zyket]

Non, pas tout à fait. La formule du volume de l'aire, A, d'un disque de rayon r c'est le produit de pi et du carré du rayon : A=pixr²

[nahz]

donc V=1/3(PI*(R²+x²))*(R+x) c'est bon?

[zyket]

Oui
Attention il faut bien garder la notation V(x)=1/3(PI*(R²-x²))*(R+x) et non pas comme un peu vite écrit V=1/3(PI*(R²+x²))*(R+x)
V(x) c'est le volume du cône en fonction de x.
En langage mathématique on peut appeler V la fonction qui à un réel x associe le volume du cône V(x)=1/3(PI*(R²-x²))*(R+x)

Il ne reste plus qu'à étudier cette fonction V, en réécrivant V(x) sous la forme d'un polynôme de x, comme on étudie n'importe quelle autre fonction, :
- son domaine de définition (ici d'après le schéma x peut varier entre quelles valeurs ?)
- la recherche de ses extremums (minimum ou maximum) dans son domaine de définition grâce à l'étude de sa dérivée.

Donc première chose à faire réécrire V(x) sous la forme d'un polynôme de x

[nahz]

J'ai pas vraiment compris pouvez-vous me donner un exemple??

[nahz]

V(x)=1/3(PI*(R²-x²))*(R+x)
=1/3(PIR²-PIx²)(R+x)
=(1/3PIR²-1/3PIx²)(R+x)
=1/3PIR³+1/3PIR²x-1/3PIx²R-1/3PIx³
=?????

[zyket]

A priori oui, je n'ai pas vérifié le développement.

Donc V(x) est un polynôme du troisième degré du type V(x)=ax^3+bx^2+cx+d.
Donc la dérivée V' de la fonction V est telle que V'(x)=3ax^2+2bx+c

Avec a=...... ; b=........ ; c=.......

Pour trouver les extremums on doit résoudre V'(x)=0, donc l'équation du second degré 3ax^2+2bx+c=0

[nahz]

Mais j'arrive pas à développer cette équation avec les puissances, aider moi SVP

[zyket]

=1/3PIR³+1/3PIR²x-1/3PIx²R-1/3PIx³

Mais ça y est ton expression est développée

1/3PIR³ est un nombre fixe qui ne dépend pas de x
1/3PIR²x est un nombre qui dépend de x du type cx
1/3PIx²R est un nombre qui dépend de x² du type bx²
1/3PIx³ est un nombre qui dépend de x³ du type ax³

Donc V(x)=ax³+bx²+cx+d avec a=.... ; b=..... ; c=....... et d=....... (attention aux signes)

[nahz]

V(x)=-1/3PIx³-1/3PIx²R+1/3PIR²x+1/3PIR³
c'est bon???
a=-1/3PI
b=-1/3PIR
c=1/3PIR²
d=1/3PIR³

[nahz]

donc V'(x)=3*(-1/3PI)x²+2*(-1/3PIR)x+1/3PIR
V'(x)=-PIx²+2/3PIRx+1/3PIR
ensuite
V'(x) = 0
-PIx²+2/3PIRx+1/3PIR = 0

c'est bon??? et ensuite j'utilise le trinôme???

[gg0]

il y a un carré oublié à la fin du V'

[nahz]

A oui, sa va faire, en plus je me suis trompé dans les signes
V'(x)=-PIx²-2/3PIRx+1/3PIR²
ensuite
V'(x)=0
-PIx²-2/3PIRx+1/3PIR²=0 et maintenant je dois utilisé le trinôme????