Bonjour,
Je cherche une personne bienveillante pour me résoudre cette question ( la résolution de celle-ci me permettrait de comprendre l'exercice ) :
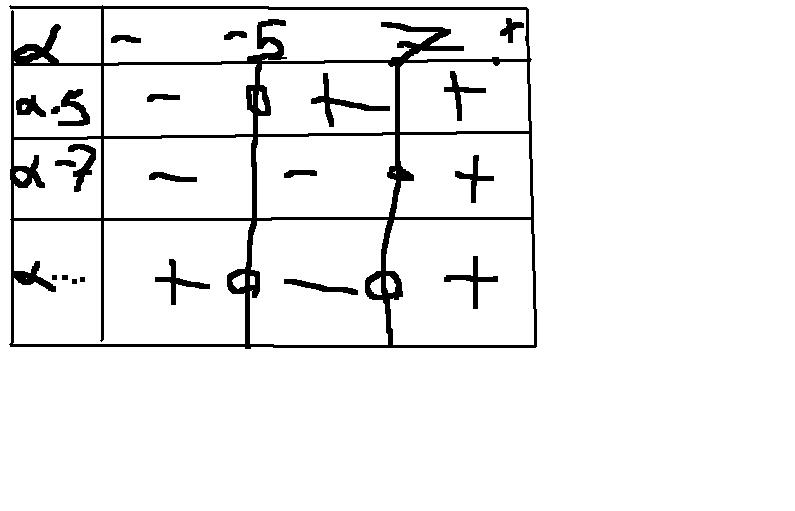
"Déterminer tous les nombres réels tels que -5<( est plus petit que )x²+6x( est plus petit ou égal à ) 7
Voilà, je suis dans le brouillard
{-5; ???????;7}
Bonsoir,
Tu as juste à résoudre le système d'inéquations suivant :Envoyé par cocobongo
Tu cherches les racines de ces 2 polynômes (si elles existent), tu étudies le signe de ces 2 polynômes en fonction des racines existantes en consignant tout çà dans un tableau, tu recoupes les 2 résultats, ... et c'est fini !
Cà veut dire quoi çà ??
Dernière modification par PlaneteF ; 16/08/2012 à 23h27.
Donc,
x²+6x+5 ( est plus grand que ) 0
x²+6x-7 ( est plus petit ou égal à ) 0
Aux similitudes, on peut éliminer les deux premiers et on obtient :
Pour le premier polynôme : x=-5
Pour le deuxième polynôme : x=7
Est-ce bien ça ?
Déterminer tous les nombres réels revient à déterminer le domaine de définition ?
Donc, d'après le tableau,
Df R = [-;-5[ ]7;+]
Je m'y approche ?
Désolé pour l'image, c'est fait en express tgv et la souris n'est pas optimale
Bonjour.
Et même, come les équations ont été écrite 2 fois, éliminer les équations, c'est à dire le problème !!Aux similitudes, on peut éliminer les deux premiers
Bon, sois sérieux : -5 vérifie-t-il la première inéquation ? d'ailleurs tu as obtenu les inéquations
5>0
-7<=0
qui ne disent rien de x.
Donc il faut arrêter d'écrire pour commencer par vraiment réfléchir. Et traiter le problème sans te débarrasser des questions par du baratin.
Essaie déjà de trouver tous les x tels que. Si tu as besoin de traiter cette question, tu as eu à apprendre à le faire (*). Au fait, tu es à quel niveau ?
Cordialement
(*) Ce qui ne veut pas dire que tu l'as appris, mais c'est le moment de t'y mettre.
Suppression pour cause de croisements de messages !
Dernière modification par PlaneteF ; 20/08/2012 à 17h40.
Je suis de 4ème, je dois passer un examen d'admission universitaire me permettant d'outre passer la question du CESS
Je n'ai pas appris à faire ce genre de calculs mis à par par moi-même
Je connais les équations, les inéquations, les systèmes d'équation, mais les systèmes d'inéquations du second degré, je ne connais pas !
Selon ma méthodologie, la résolution textuelle de celle-ci serait bienvenue car me permettrai de comprendre comment procéder
Ok,
je comprends mieux. Mais ce n'est pas en faisant un exercice de ton "formulaire de questions" (liste d'exemples d'exercices) que tu sauras faire. Il faudrait que tu étudies les ouvrages des classes qui te manquent, car même si on te rédige un corrigé, il te manque trop de connaissances pour arriver à comprendre de quoi on parle.
Donc étudie dans un bouquin la résolution des équations du second degré, la règle du signe d'un trinôme du second degré, et son application aux inéquations du second degré.
Bon courage !
Merci
J'ai un problème avec les tableau de signes
J'ai étudié le cours sur les tableau de signes de CMATH.FR mais je ne comprends pas, à la dernière ligne du tableau comment interpréter les + et - ( j que je sais correctement placer ) pour écrire la solution finale
Un cours web serait le bienvenu ! merci
Ici, tu n'as pas besoin d'utiliser les tableaux de signes (n'imite pas ce que tu ne comprends pas, cherche ce qui a un sens dans ta situation). Seulement les signes des trinômes x²+6x+5 et x²+6x-7 pour savoir quelles valeurs de x satisfont chacune des inéquations. Ensuite, il te faudra dire quels sont les valeurs de x pour lesquelles les deux inéquations à la fois sont vraies (c'est ça un système).
Sinon, généralement, on utilise les tableaux de signes pour trouver le signe d'un produit ou d'un quotient, ou d'un quotient de produits. C'est une façon de présenter rapidement, en appliquant la règle des signes. Donc c'est tout simple.
Cordialement.
quelle est la différence entre un polynôme et un trinôme ?
Un trinôme est un polynôme du 3ème degré ?
x²+6x+5>0 ( delta = b²-4ac ) = 36x²-4.x².5 = 36x²-20x² = 16x² ( delta > 0 donc l'équation admet 2 solutions )
x1 = -6x - racine de 16x² / 2x² = -6x-4x/2x = -10/2 = -5
x2 = -6x + racine de 16x² / 2x² = -2x / 2x² = -1
L'inéquation suivante : x²+6x+5>0 admet 2 solutions : -5 et -1
Est-ce que je m'y approche ? J'ai des doutes concernant un numérateur x simple sur un dénominateur x au carré ?
Si cette méthode est exacte, je trouve pour x²+6x-7 les solutions :
x1 = 7
x2 = 1
Je pense avoir fait une erreur : que vaut 2x/2x² ? Est-ce que cela reviendrait à faire 2.(1) / 2.(1)² ? Dans ce cas la, ce serait 2/2 donc 1 ? ( désolé, je ne pouvais pas éditer)
Présenté comme tu le fais, c'est faux. Lorsque tu calcules le delta puis les racines, x n'intervient pas !
Ici tu as : a=1 ; b=6 ; c=5 ... il n'y a pas de x !
Non, c'est l'équation x2+6x+5=0 qui admet les 2 solutions : -5 et -1
Dernière modification par PlaneteF ; 21/08/2012 à 16h54.
Il faut donc remplacer x par 1 ?
( Est-ce que ce calcul a un rapport avec celui-ci : http://www.cmath.fr/1ere/equations2e.../exercice5.php il faut cocher une réponse au pif afin d'avoir la correction de celui-ci )
Non absolument pas ! ...c'est l'inconnue, c'est ce que tu recherches !
Tu as tout simplement :
Dernière modification par PlaneteF ; 21/08/2012 à 17h07.
D'accord, c'est très simple en fait, relativement.
Je refais les calculs
delta = b²-4ac = 6²-4x1x5 = 16 > 0 donc 2 solutions
Je ne comprends pas, en refaisant les calculs, j’obtiens les mêmes réponses
la formule de delta est bien que si delta est positif alors il y a 2 solutions dont la formule est :
x1 = -B-racine de delta / 2A
et x2 = -b+racine de delta / 2A
C'est bien ça ?
((((((je me suis trompé de dénominateur, 1 au lieu de 2 ((((((((((((((((((((
x1 = -10
x2 = -2
et delta de 6²-4x1x(-7) = 64 > 0 donc 2 solutions :
x1 = -14
x2 = 2 )))))))))))))
Les 2 racines x1=-5 et x2=-1 que tu avais trouvées tout à l'heure étaient correctes, je ne te disais pas le contraire, ... c'est juste que le calcul que tu avais présenté en y faisant apparaître l'inconnue x qui n'avait absolument rien à faire là, ... et bien ce calcul, du coup, était faux !
Non c'est faux.
Dernière modification par PlaneteF ; 21/08/2012 à 18h28.
Ouf, d'accord donc les solutions suivantes sont justes :
-5 et -1
-7 et 1
Ensuite, à cette étape, n'est-il pas question d'un tableau de signe ?
C'est comme tu veux, ... le tableau de signes c'est juste un moyen de représentation visuel, très pratique, ... mais tu peux aussi faire sans, si tu te sens à l'aise !
Dans tous les cas de figure, la première inéquation aura pour solution S1, la deuxième S2 ... et donc la solution finale sera l'intersection de ces 2 ensembles.
Dernière modification par PlaneteF ; 21/08/2012 à 18h50.
Donc la solution de la question "Déterminer tous les nombres réels tels que -5 (est plus petit que) x²+6x ( est plus petit ou égal à ) 7 est :
La première équation S : ]-5;-1[
La deuxième équation S : ]-7;1[
et l'intersection entre ces deux solutions est : ]-5;-1[
C'est çà ?
( comment fais-tu pour pour écrire les caractères spéciaux comme delta ou S exposant 1, ect ? )
Non c'est faux. Quelle est la règle du signe d'un trinôme du 2nd degré ?
Presque juste, ... mais donc faux ! --> L'inéquation est un "inférieur ou égal" !
Dernière modification par PlaneteF ; 21/08/2012 à 19h07.
Est-il question de factorisation ?
Pour trouver la règle en question oui :
Supposons que l'équation
Alors :
Donc si tu fais un tableau des signes, tu verras que dans ce cas le trinôme
Je te laisse donc appliquer cette règle au trinôme
Dernière modification par PlaneteF ; 21/08/2012 à 21h02.
Mon tableau de signe conclu :
- 1 5 +
____________________________
- 0 + +
- - 0 +
+ 0 - 0 +
J'ai un soucis pour retranscrire le tableau, la dernière ligne dit + 0 - 0 + ( pour -;1;5;+ )
Donc, (c'est à cette étape que j'ai des lacunes) comme tu as dis, la solution est tout sauf l'intersection entre 1 et 5 donc :
]-;1[U]5;+[ c'est ça ?
Ben non, vu que les 2 racines sont : -5 et -1
Dernière modification par PlaneteF ; 21/08/2012 à 21h31.
donc c'est :
]-;-5[U]-1;+[
c'est correct ?
C'est bon, ... c'est OK pour S1 !
Maintenant il faut trouver S2 ...
Dernière modification par PlaneteF ; 21/08/2012 à 21h35.
S2 = ]-;-7]U]1;+[
Correct ?
