Vecteurs

[Flof54]

Bonjour à tous,

je suis totalement bloqué à l'exercice suivant :



Je ne comprends même pas la consigne, et donc, par conséquent, je ne connaît pas la méthode pour le faire.

Pourriez-vous m'éclairer SVP ?

Merci d'avance !
-----

[gg0]

Bonjour.

Tu as deux questions, correspondant à deux dessins. Prenons le premier. Tu connais et , ils sont représentés. Avec ces deux vecteurs et , tu peux calculer et . Vois-tu le calcul ?

Calcul analogue : tu sais que a+b = 7 et a-b = 1. Combien vaut a ? Pense à le faire directement (pas par substitution) par combinaison des deux égalités (c'est très facile !)

Cordialement.

NB : la consigne est claire, il te manque simplement de bien comprendre "dans les deux cas suivants".

[Flof54]

D'accord. En fait il faut résoudre un système d'équation.

v+u = 12 cm
v-u = 4.5 cm

v = 12-u
(12-u)-u = 4.5

v = 12-u
12-u-u = 4.5

v = 12-u
12-4.5 = 2u

v = 12-u
7.5/2 = u

v = 12-u
u = 3.75

v = 12-3.75 = 8.25
u = 3

Le système a pour solution le couple (8.25 ; 3).

Donc v = 8.25 et u = 3

Est-ce que cela est juste ?

[Lucien-O.]

Ah non!
Ici on te demande une résolution "géométrique".
Il existe une règle simple, dite "du parallélogramme", qui permet d'effectuer l'addition de deux vecteurs : http://www.educastream.com/vecteurs-seconde.

[A voir en vidéo sur Futura]

[Flof54]

Alors qui dois-je croire ?

L'un me dit qu'il faut résoudre a+b=7 et un autre qui me parle de règle du parallélogramme...

[gg0]

Bizarre :

Où as-tu trouvé "v+u = 12 cm" ? Les cm mesurent les longueurs réelles, u est un vecteur, donc un objet abstrait. On peut le représenter et il a une longueur, mais n'est pas une longueur.
Il serait peut-être bon de reprendre ton cours avec ton cahier et ton livre, car pour l'instant tu ne sais pas de quoi on parle (je comprends mieux le "Je ne comprends même pas la consigne" puisque tu n'as pas appris ce qu'est un vecteur !

Bon travail !

[Flof54]

Dans la relation du parallélogramme, il n'est pas question de u-v...

[gg0]

Par définition,

u-v=u+(-v).

[Flof54]

OK. Je commence à comprendre...

[Flof54]

Et donc, dans ce schéma de la relation du parallélogramme, j'ai représenté les vecteur u et v.
Et c'est ce qui m'est demandé dans cet exercice.

[gg0]

Je ne vois ni ni . Ni aucun rapport avec les consignes de l'énoncé.

Tu joues à quoi ?

NB : Si tu espères qu'ainsi tu finiras par obtenir que quelqu'un te fasse l'exercice, tu montres simplement que tu ne mérites pas qu'on t'aide.

[Flof54]

J'ai fais une erreur : sur ce schéma j'ai représenté les vecteurs a et b. Mais c'est le bon raisonnement non ?

Je n'apprécie pas tes propos sur moi. Je demande juste de l'aide, pas qu'on me fasse l'exercice ! Où tu vas chercher ça ? OK je fais de grossières erreurs mais les vecteurs ça n'a jamais été mon truc !

Si ça te dérange d'aider les gens, tu n'as rien à faire sur ce forum !

[Lucien-O.]

Euh, tu te trompes lourdement sur le compte de gg0,...
Il est presque chaque fois disponible pour répondre aux questions; tu n'as qu'à consulter les autres conversations et tu constateras qu'il a déjà éclairci bien des sujets!

Soit, revenons à ton problème.
On peut supposer en voyant ton dessin que tu as compris la méthode du parallélogramme, mais tu as oublié d'orienter tes vecteurs et un vecteur non orienté c'est pas un vecteur,...Passons.
Si tu as compris la méthode, tu sauras représenter et pareillement .
Tu te rappelleras que multiplier un vecteur par un scalaire (un nombre qui n'est pas un vecteur, comme 2 par exemple) revient à multiplier sa norme et éventuellement à changer son sens si le nombre est négatif.
Avec ces infos là, ça devrait rouler!

Bon travail.

[Flof54]

Merci Lucien-O. Concernant, gg0, peut-être que je me trompe mais là je me défends car il m'a manqué de respect.

Enfin, j'ai compris ce que tu m'as dis dans ton message. Mais là il est question de représenter les vecteurs u et v dans chaque cas. Il faut donc les tracer. Et pour cela, il faut avant tout tracer un parallélogramme, non ?

[Lucien-O.]

Non.
Le parallélogramme tu le construis à partir des vecteurs que l'on te donne (ces vecteurs constituent deux des cotés de la figure).
En fait, tu viens placer l'origine d'un second vecteur sur l'extrémité d'un premier vecteur et le point que tu obtiens est l'extrémité de ton vecteur somme.
Pour imager un peu tu peux considérer le vecteur comme une translation.
Additionner deux translations, c'est faire la première et puis faire la seconde à partir de l'endroit où la première t'a menée; donc c'est aller vers un point puis vers un second ce qui revient à aller d'un seul coup vers le second point (la fameuse loi de Chasles AB+BC=AC)! C'est ce que fait ton vecteur somme.

Ps: Je me relis et je réalise que j'ai sans doute mal compris :

Et pour cela, il faut avant tout tracer un parallélogramme, non ?

J'ai cru comprendre que tu voulais tracer un parallélogramme un peu n'importe où,...Ce qui n'aurait aucun sens bien sûr. Bref, oui la première étape est de construire le parallélogramme! Désolé.

[Flof54]

Est-ce que je suis sur la bonne voie ?

[Lucien-O.]

Non, c'est pas ça.
Relis attentivement ce qui a été dit.

Bonne soirée!

[Flof54]

J'ai trouvé.

[Lucien-O.]

Non, c'est toujours pas correct, le segment (ce ne sera pas un vecteur tant que tu oublieras de l'orienter,...) jaune a une longueur qui correspond à 2u et comme les diagonales d'un parallélogramme se coupent en leur milieu on peut imaginer que tu as voulu diviser ce segment en deux mais rien ne nous indique que c'était ton intention, comment veux tu que l'on devine?
J'imagine, mais je ne suis même pas sûr que tu proposes bien cette ligne jaune comme solution,...
En fait, le seul vecteur que tu ais dessiné est celui parallèle à u-v, pour moi ça signifie que c'est ta solution et c'est complètement faux alors,...
En plus, je ne vois pas ce que représente le triangle de base u-v collé à ta figure.

Bon,...Faudrait quand même que tu lises attentivement ton cours, que tu observes les exemples et que tu rédiges avec précision ta réponse parce que là c'est vraiment le bazar!
La solution n'est pas compliquée et tu as tous les éléments pour y aboutir.

Bon travail !

Ps: Avant de poster, essaye de réfléchir un peu plus par toi même!

[Damsaon]

A l'auteur du pb :

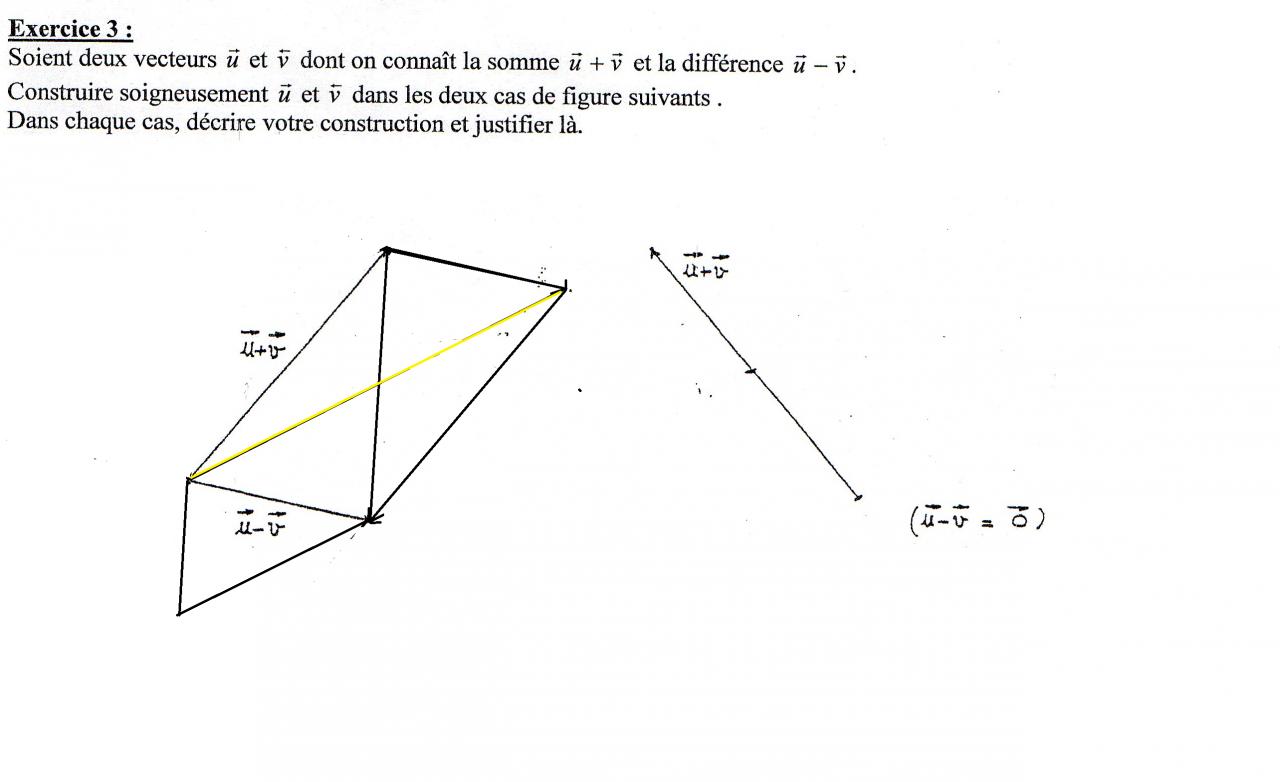
Prends l'exemple de gauche, deux vecteurs sont tracés. Le premier vecteur correspond à la somme d'un vecteur u et d'un vecteur v. Le second vecteur correspond à la différence entre les mêmes vecteurs u et v.

Toujours sur cet exemple de gauche, dessine géométriquement la somme des deux vecteurs qui sont dessinés en utilisant la règle du parallélogramme. Puis exprime cette somme en fonction des vecteurs u et v. Et garde en tête que l'objectif de l'exercice est d'obtenir un tracé des vecteurs u et v

[Flof54]

Réponse cas 1 : Grâce à la loi du parallélogramme, on a : (u+v)+(u-v) = 2u et v = (u+v)-u

Réponse cas 2 : Etant donné que les vecteurs u et v ont le même sens et que leur différence est nulle, on peut déduire que ces vecteurs sont de mêmes normes et colinéaires donc confondus.

[gg0]

Ah, on avance !

Pour la question 1, tu n'as pas dit comment on obtient , et tu ne l'as pas représenté sur le dessin. Donc un effort pour faire une vraie réponse (la construction de reste aussi à faire).
Question 2 "les vecteurs u et v ont le même sens" Ah non ! Revois ton cours sur les vecteurs pour comprendre ce qui se passe quand la somme de deux vecteurs est nulle.

Cordialement.