Simplifier une dérivée

[curieuxdenature]

Bonjour

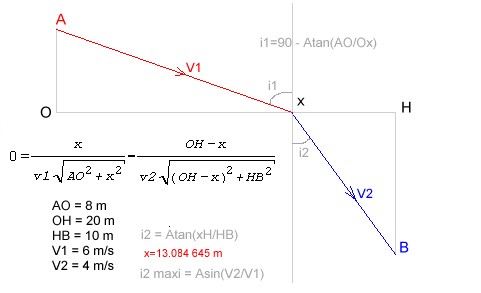
j'essaye sans succès de simplifier cette équation pour en extraire x :




par itérations je parviens au résultat, mais le but est d'éviter de se farcir toutes les valeurs de x pour tomber sur la valeur 0.
Autrement dit je désire arriver à x = ?
Et là, je coince, les neurones de papy font de la résistance ...

je vous donne une application numérique si ça peut servir à mieux cerner la donne.

AO : 8 m
OH : 20 m
HB : 10 m
v1 : 6 m/s
v2 : 4 m/s

x= 13.084 m



c'est une version du maitre-nageur pour illustrer la réfraction de la lumière entre deux milieux d'indice différent où on demande quel est le plus court chemin.

Merci à ceux qui se pencheront sur mon petit problème.


-----

[joel_5632]

bonjour



puis en élevant au carré, les racines disparaissent non ?

mais ça conduit à une équation du 4 ème degré ...

[Damsaon]

Salut!
C'est quoi la question exacte telle qu'elle est formulée dans ton exo ?

[curieuxdenature]

Bonjour Damsaon

la question est de trouver x en fonction des variables.
sinon j'avais bien ça :





je ne suis pas sorti de l'auberge.

[A voir en vidéo sur Futura]

[curieuxdenature]

bonjour



puis en élevant au carré, les racines disparaissent non ?

mais ça conduit à une équation du 4 ème degré ...

Merci, je vais voir si je m'en sors avec ça

[gondebaud]

Bonjour

bonjour



puis en élevant au carré, les racines disparaissent non ?

mais ça conduit à une équation du 4 ème degré ...

Malheureusement, la racine carrée dans le second membre ne "disparaîtra" pas facilement, du fait de la présence du terme 100.
Sinon, prendre garde qu'en élevant les deux membres au carré, il y aura deux cas à considérer (A²=B² <=> A=B ou A = -B).

Cordialement.

EDIT : Oups, rien dit, mal vu la racine dans le second membre :/.

[gg0]

Mais si, Gondebaud,

le 100 est sous la racine carrée.
Il n'est pas obligatoire de considérer deux cas, les deux membres doivent être de même signe, simplement. Or x est une valeur comprise entre 0 et 20, ce qui fait que x et 20-x sont bien de même signe.
D'ailleurs, on peut élever au carré sans souci, en n'oubliant pas à loa fin de "vérifier les solutions", car on n'a pas procédé par équivalence.

Cordialement.

NB : On tombe sur une équation de degré 4 pas particulièrement réjouissante.

[curieuxdenature]

Bonjour

je pense que ça ne va pas être exploitable :



il sera plus rapide (en temps de calcul) de tracer les deux courbes et de recouper le point zéro.
Merci pour vos idées en tous cas, c'est sympa.

[Damsaon]

Rassure moi, c'est pas niveau lycée comme exo ?

[joel_5632]

Je te conseille la lecture de cette page de wikipédia sur le principe de Fermat qui permet de démontrer la loi de Descartes sur la réfraction en optique n1.sin(i1) = n2.sin(i2)
http://fr.wikipedia.org/wiki/Princip...nell-Descartes

Ton problème est analogue, je pense qu'il faut juste remplacer n1 par 1/v1 et n2 par 1/v2

donc v2.sin(i1) = v1.sin(i1)

et zut ... on retombe exactement sur la même équation à résoudre.



pourtant j'ai déjà vu cet exercice

[Damsaon]

Joel : on ne "remplace" pas n1 par 1/v1 : ce que l'on calcule est un temps minimum, soit t = t1 + t2 (1 : milieu 1, 2 : milieu 2) = d1/ v1 + d2/v2 et comme v1 = c/n1 et v2 = c/n2, tu peux virer les c en dérivant l'expression de la durée

[joel_5632]

en optique n1/n2 exprime le rapport v2/v1 des vitesses de la lumière dans les milieux 1 et 2 (car v = c/n) donc sur la plage je mets bien v2 à la place de n1 et v1 à la place de n2. je retrouve exactement la formule qui annule la dérivée, ce doit être juste

[gondebaud]

Bonjour,

Mais si, Gondebaud,

le 100 est sous la racine carrée.
Il n'est pas obligatoire de considérer deux cas, les deux membres doivent être de même signe, simplement. Or x est une valeur comprise entre 0 et 20, ce qui fait que x et 20-x sont bien de même signe.
D'ailleurs, on peut élever au carré sans souci, en n'oubliant pas à loa fin de "vérifier les solutions", car on n'a pas procédé par équivalence.

Cordialement.

NB : On tombe sur une équation de degré 4 pas particulièrement réjouissante.

Oui, c'est exact. Pour le 100, je m'en suis aperçu après avoir envoyé ma réponse et j'ai rajouté un edit dans les 5 minutes imparties.
Pour la méthode de mettre les membres au carré, on obtiendra effectivement toutes les solutions justes et d'autres solutions en trop (A=B => A²=B² mais du coup dans A²=B², on a aussi les solutions de A = -B).
Donc, en résumé, mon message était une belle ânerie .

Sinon, si cette équation de degré 4 n'est pas réjouissante alors on sera coincé si on ne trouve pas 2 racines ou un diviseur polynomial de degré 2 sans racines réelles.
Cordialement

[gg0]

Bonjour.

Généralement, il n'y a pas d'expression simple de la racine utile (physiquement, il me semble qu'il n'y en a qu'une, et mon esclave formel me le confirme). C'est bien pour ça que la loi de Snell (avec les sinus) est l'outil classique.
Car Joël a raison : la traduction des vitesses en indice ramène le problème des vitesses en un problème d'indices.

Cordialement.

[curieuxdenature]

Rassure moi, c'est pas niveau lycée comme exo ?

Bonjour

je pense que si pour l'exercice, c'est de l'optique géométrique dans la partie à résoudre, le calcul du temps de trajet minimum m'a l'air assez simple, Pythagore suffit.

Eliminer 't' en dérivant est la portée d'un niveau Bac je présume.

[curieuxdenature]

Bonjour.

Généralement, il n'y a pas d'expression simple de la racine utile (physiquement, il me semble qu'il n'y en a qu'une, et mon esclave formel me le confirme). C'est bien pour ça que la loi de Snell (avec les sinus) est l'outil classique.
Car Joël a raison : la traduction des vitesses en indice ramène le problème des vitesses en un problème d'indices.

Cordialement.

Bonjour

j'avais vu le rapport avec les indices de réfraction, et j'avais trouvé rapidement la solution en traçant les deux courbes mais je pense que j'ai placé la barre un peu haut en voulant trouver une expression unique de x pour tous les cas de figure, l'équation doit être longue comme un jour sans pain (ou sans vin)

maitre-nageur.jpg
ça peut servir :

Fermat.jpg

[ansset]

Bonjour

je pense que si pour l'exercice, c'est de l'optique géométrique dans la partie à résoudre, le calcul du temps de trajet minimum m'a l'air assez simple, Pythagore suffit.Eliminer 't' en dérivant est la portée d'un niveau Bac je présume.

Je ne sais pas, j'obtiens la même équation que celle présentée au départ et même en simplifiant:
j'obtiens: avec y =x/OH
(1-y)/y= (2/3) * rac(((1/2)²+(1-y)²)/((2/5)²+y²)) soit
(1-y)²/y²= (2/3)² *((1/2)²+(1-y)²)/((2/5)²+y²))

donc si la mise en équation est du niveau lycée, sa résolution semble plus complexe.
je n'ai rien vu d'évident la dedans.

[ansset]

oui trouver une solution graphique ! mais ce n'est pas resoudre le pb analytiquement.
en simplifiant encore et en posant u=y/(1-y) j'arrive à une équation de degré 3 en u , c'est mieux qu'une équation de degré 4, mais ce n'est pas encore ça.

[curieuxdenature]

merci ansset, si ça dépasse le cadre lycée, je m'en excuse, il y a longtemps que j'ai quitté l'école, j'ai sauté de la 5eme au Collège technique...

C'est bien ce genre de simplification qui me turlupine (poser y=x/OH et ensuite u=y/(1-y) ne me saute pas au yeux...), je m'attendais à plus réjouissant.
Je vais potasser ça.


----
pour ne pas induire en erreur, je tiens à signaler une erreur dans le deuxième graphe :
"il faut que t1=t2 (Ax/V1 = xB/V2" est une bourde, c'est plutot dt1/dx = dt2/dx les deux temps ne sont pas égaux.

[ansset]

pas de soucis,
en plus, moi j'ai fait une erreur de calcul.
le post #18 n'est pas à prendre en compte...
mais il y a peut être une solution en trouvant un bon changement de variable.