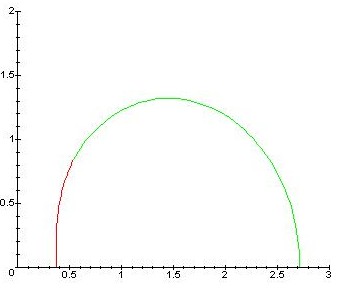
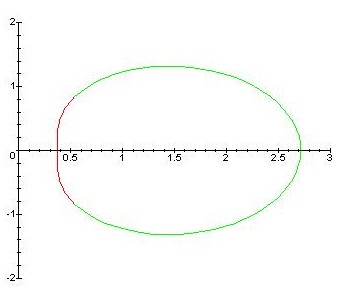
Détermination d'ensemble - Module de logarithme complexe
Discussions similaires
-
Par inviteab4b845d dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 29/09/2012, 12h27
-
Par invitead88f3c2 dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 15/09/2010, 18h24
-
Par invite4b5e6d8a dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 06/09/2009, 14h26
-
Par invitee84581f6 dans le forum Mathématiques du collège et du lycée
Réponses: 4
Dernier message: 08/01/2009, 10h28
-
Par invite9c9b9968 dans le forum Mathématiques du supérieur
Réponses: 5
Dernier message: 25/02/2005, 16h34
.
, alors
.