Bonjour ,
Je poste ici afin d'obtenir de l'aide sur un exercice assez difficile sachant qu'on vient de commencez ce chapitre en cours .
J'ai posté en pièce jointe l'énoncé et ce que j'ai fait sur cette exercice ,pour que ça soit plus clair.
Merci d'avance
Cordialement
Tu as été jusqu'où pour le moment ? Qu'as-tu fait ? As-tu des idées ?
Merci pour votre réponse ,ce que j'ai fais a été mis en piece jointe
Bonjour,
Pour la première question, vous partez dans tous les sens et ça ne veut pas dire grand chose.
Dans l'énoncé on vous définit une suite In (avec un i majuscule pas un l minuscule), vous la renommez ln ce que vous écrivez exactement de la même façon que la fonction logarithme népérien "ln" que vous utilisez dans la même question. Pour s'embrouiller ça commence déjà bien.
Ensuite vous semblez vouloir définir une fonction F pour vous aider et vous dites : "F(x) = 1/(1+tn)", ce qui fait qu'à droite vous avez une fonction de x et à gauche une expression que dépend de t et de n. Vous vouliez peut-être définir des fonctions Fn par "Fn(t) = 1/(1+tn)" ?
Je vois que vous avez écris que F'(x) = ln(1+t), je suppose que vous parlez bien ici de la fonction logarithme et pas de votre suite. Mais quelque soit la manière dont on regarde F'(x) = ln(1+t) cette égalité est fausse. Déjà il y a toujours le même problème de quelque chose en x égal à quelque chose en t (et le n a disparu sans raison), mais même si on écrivais Fn'(t) = ln(1+t) ce serait toujours faux (et c'est faux quelque soit n).
La conclusion de votre première question vous mène à écrire une dernière ligne qui ne veut rien dire. Je n'arrive même pas à la décrypter et ne vois pas le lien que ça a avec ce que vous écrivez précédemment.
Ce qu'on vous demande dans cette question c'est de calculeret il faut calculer cette intégrale. Dans cette question "n" n'apparaît nul part.
Wir müssen wissen, wir werden wissen.
Excuser pour l'erreur je me suis tromper je re commence
Oups désolé, j'avais pas fait attention...Envoyé par THESO
Pas de soucis,ps:je me suis corrigé c'est mieux ?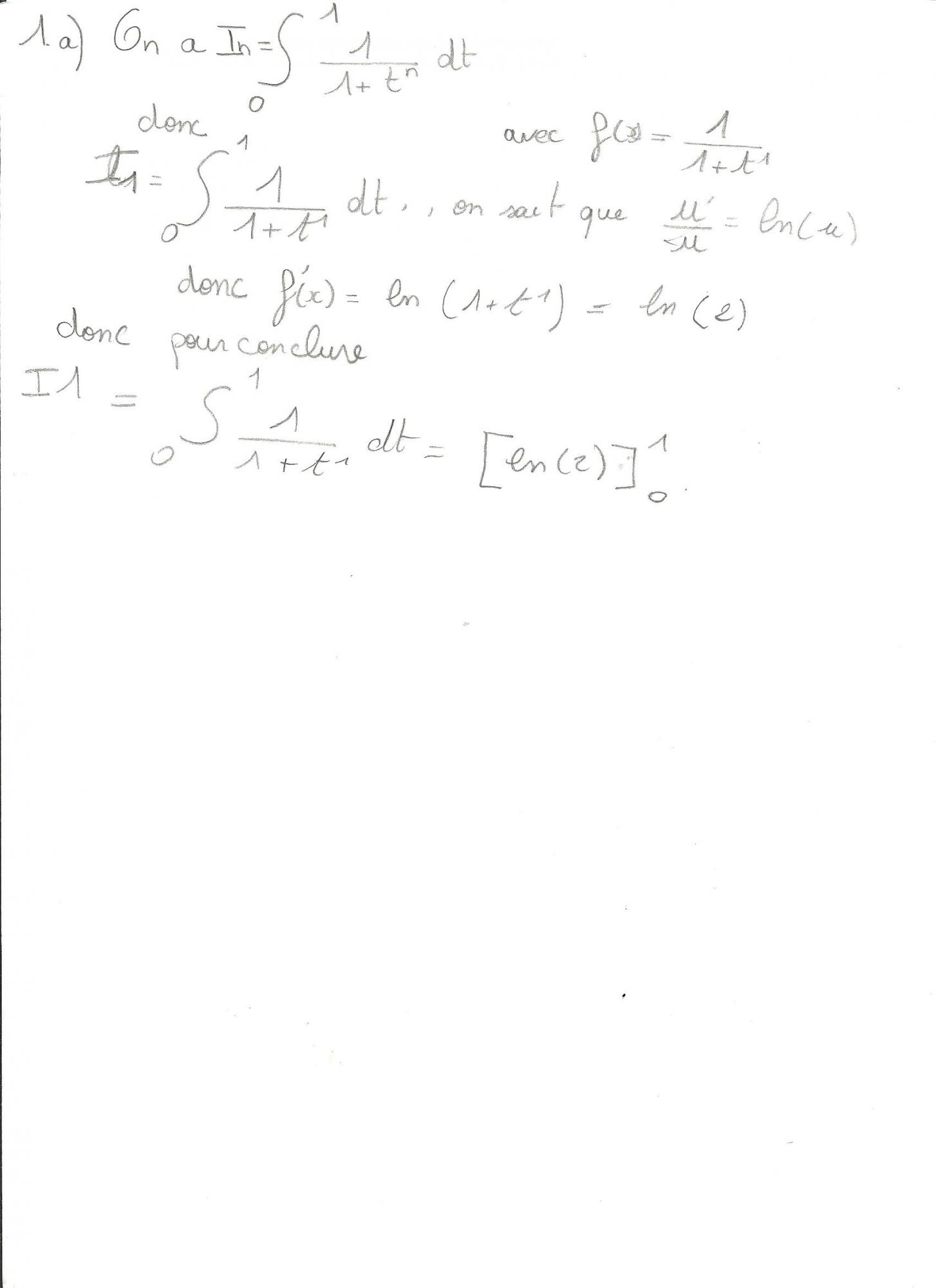
(voir piece jointe)
C'est a peine mieux, mais ça reviens grosso modo au même.
Vous écrivez de nouveau f(x)=1/(1+t), soit votre variable c'est "x" soit c'est "t" mais il faut choisir. Ensuite vous écrivez u'/u = ln(u) ce n'est pas vrai, ce dont vous voulez parler c'est de la dérivée de la fonction logarithme pas de la fonction logarithme elle-même.
Encore une fois quand vous écrivez "f'(x)=ln(1+t)" il y a ce problème de variable que vous ne corrigez toujours pas. Mais même écrire f'(t)=ln(1+t) c'est tout à fait faux. Le logarithme ce n'est pas la dérivée de la fonction inverse, revoyez la définition du logarithme et écrivez les choses dans le bon sens.
De plus vous n'avez aucune raison de chercher une dérivée de f, ce qui vous intéresse c'est de l'intégrer donc d'en trouver une primitive.
La cerise sur le gâteau c'est le "ln(1+t)=ln(2)" qui apparaît comme ça sans raison comme si t était égal à 1.
Wir müssen wissen, wir werden wissen.
Ca y est j'ai fait presque toute les question il me manque la 3a
Vu les horreurs que vous avez écrites rien que sur la question 1 à tel point que ça ne voulait plus rien dire ce serait bien de nous écrire ce que vous avez fait pour les autres questions que la 3a déjà. Histoire de pouvoir voir si vous avez effectivement compris et écrit quelque chose qui ressemble au moins un peu à des maths.
Wir müssen wissen, wir werden wissen.
J'apprécie vraiment la manière a la quelle vous me répondez je sais que je ne suis pas un crack mais respectez les posteurs ,je vous remercie pour l'aide données précédament ,je ne vous embête pas plus
Bonne soirée
Cordialement
Si ça m'embêtais de vous répondre je ne vous répondrais tout simplement pas et je ne cherche jamais à enseigner quoi que ce soit aux gens que je méprise, il faut donc que j'ai du respect pour vous pour prendre la peine de le faire.
Ma remarque précédente n'était ni une question de respect ni une question d'ennui. Le fait est que dans votre premier message sur les quatre lignes que vous prenez pour répondre à la question 1a je peux dénombrer une bonne dizaine d'erreurs distinctes et c'est sans compter l'absence d'enchaînement logique dans le raisonnement même. Si je devais corriger une copie avec ça d'écrit dessus je serais obligé de rayer d'une croix le paragraphe entier et de mettre 0.
Ensuite vous me demandez de vous aider à répondre à la troisième question alors que d'après ce que j'en sais vous n'êtes pas en mesure de répondre correctement à la première. Je pense qu'il est préférable de répondre aux questions dans l'ordre, parce que si vous ne comprenez pas le début c'est normal que vous n'arriviez pas à faire la fin.
Wir müssen wissen, wir werden wissen.
Theso a eu la chance de tomber sur le moins rigoureux de nos mathématiciens
Ceci dit, S321 a tout à fait raison, on ne nous apprend plus du tout à être rigoureux, à écrire bien les choses etc... et quand on arrive dans le supérieur c'est une catastrophe.
Bien rédiger, c'est aussi à la fois faire preuve d'une bonne compréhension de ce que l'on manipule, et à la fois... mieux comprendre soi-même ce que l'on écrit !
A fortiori dans ce genre d'exercice où la principale difficulté est de savoir de quoi l'on parle.
Tiens moi je m'étais dit qu'il avait de la chance de pas être tombé sur gg0. Parce que s'il se sent agressé par moi, j'ose pas imaginer ce que ça serait
Mais dans ce cas là je pense qu'il n'y a pas que des erreurs de rédaction, il y a aussi de vrais erreurs de raisonnement et la démonstration n'est pas seulement approximative mais véritablement fausse.
Wir müssen wissen, wir werden wissen.
Entièrement d'accord. Et tu constates ici que dire la vérité en maths est considéré par certains comme une agression. C'est que c'est de bonne foi qu'ils écrivent des énormités. Ils font des maths comme certains chantent des chansons anglaises : sans rien comprendre à ce qui est dit. Et ils tombent de haut quand quelqu'un leur dit qu'ils ne font pas des maths.Tiens moi je m'étais dit qu'il avait de la chance de pas être tombé sur gg0. Parce que s'il se sent agressé par moi, j'ose pas imaginer ce que ça serait
Cordialement.
