Bonjour,
je suis bloqué à l'exercice suivant :
Je ne sais pas par où commencer pour trouver la limite de cette fonction.
Je sais déjà que la limite de x^3+ax²+ax quand x tend vers + l'infini est + l'infini et que la limite de -x racine de (x+1) quand x tend vers + l'infini est - l'infini.
C'est cette histoire de valeurs de a qui me pose problème.
Pourriez vous m'aidez svp ?
Merci
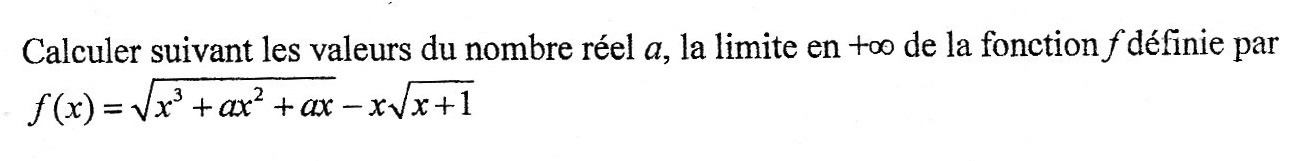
Salut,
Effectivement tu as une forme indéterminé de la forme "+00 -00 " . Si tu veux lever l'indétermination dans une expression avec des racines tu peux utiliser la partie conjugué.
D'accord.
Reste maintenant à régler pas le problème des "valeurs de a"...
Tu vas voir que si tu factorises au numérateur et au dénominateur ta limite va dépendre de a (tu as deux limites possibles au final)
j'ai factorisé le numérateur par x² ce qui donne x²(a/x+a/x²+1)
j'arrive donc à ceci
(x²(a/x+a/x²+1))/(racine de x^3(racine de(1+ax²/x^3+ax/x^3))-xracine de (x+1))
Est-ce juste ?
Si oui que dois-je faire maintenant ?
Bonsoir.
Envoyé par Flof54
Quelle expression as-tu pour f(x) après avoir multiplié par l'expression conjuguée au dénominateur et au numérateur ?
Duke.
Dernière modification par Duke Alchemist ; 01/11/2014 à 20h22.
J'obtiens (ax²+ax-x)/(racine de (x^3+ax²+ax)+xracine de (x+1))Quelle expression as-tu pour f(x) après avoir multiplié par l'expression conjuguée au dénominateur et au numérateur ?
en sortant le x² de la première partie celà donne
-
soit en négligeant le a/x en +l'inf
x(
à toi de conclure.
Cdt
désolé pour mon TEX en peu en vrac
en fait il y a trois solutions en fonction de a.
Re-Au numérateur, je trouve ax²+ax-x² et en regroupant les termes suivant les puissances de x, on obtient la condition sur a.
Duke.
EDIT :
Je suis d'accord sur ce point.
Dernière modification par Duke Alchemist ; 01/11/2014 à 20h48.
Qu'est-ce que tu appelles "la condition"?on obtient la condition sur a.
Re-
"a" est un paramètre : sa valeur influe sur la limite de la fonction f.
Le terme de condition a été maladroitement choisi
Regarde bien le numérateur, il y a bien une valeur de a qui modifie ("simplifie") de manière assez conséquente la fonction f => une limite.
Les deux autres limites sont quand...Cliquez pour afficher
Duke.
Est-ce que la valeur recherchée est 1 ?
Re-
Peux-tu affirmer au lieu de poser la question, stp ?
Quelle autre valeur veux-tu que ce soit ?
Allez, il n'y a plus qu'à déterminer les limites !
Here we go ! dixit Mario
Duke.
Si a=1, alors la limite de ax²+ax-x² quand x tend vers +00 est +00
Si a<1 alors la limite de ax²+ax-x² quand x tend vers +00 est -00
Si a>1 alors la limite de ax²+ax-x² quand x tend vers +00 est +00
oui pour moi ! sauf pour a=1 la limite vaut 0
Cdt
Heu ...
Si a=1, alors la limite de ax²+ax-x²=x quand x tend vers +00 est +00
C'est correct.
Mais peut-être fais-tu référence à autre chose.
Cordialement.
Voici donc ma réponse complète :
Ma réponse est elle correcte ?
Dans ce que tu as écris tout est correct , seulement on te demande la limite de f en +00 , pas juste la limite du numérateur
non j'ai mal lu ce qu'il avait ecrit.
je pensait qu'il parlait de la limite de l'ensemble de sa fonction et pas de la première partie uniquement.
Mais la limite de x²(a+a/x-a) lorsque a=1 vaut 0. Du coup ça ne marche pas...
Avant même de commencer il faudrait expliquer pourquoi la fonction est toujours définie quelque soit a, à partir d'un x assez grand.
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
En fait, dans tous les cas, même en factorisant par x², j'obtiens une limite indéterminée car je trouve 0 au numérateur.
comment celà ? peux tu nous montrer ton calcul.?
sinon, je n'aime pas trop contre indiquer une direction proposée, mais la multiplication par le conjugé ne simplifie pas vraiment l'exercice.
soit pour x>0
ce qui permet à la fois de trouver aisement la limite ( y compris quand a=1) et de répondre à la question de Mediat sur la définition de la fonction.
Donc la fonction f est définie sur ]0;+00[
non, celà dépend de la valeur de a.
Pour conclure :
La limite de f(x) = +00 si a>1
Lim f(x) = 0 si a=1
Lim f(x) = -00 si a<1
