DM de maths dérivation

[invite3ec2ccd8]

Bonjour, j'ai un DM a rendre prochainement et je bloque à une question, j'ai besoin de votre aide...

Voici l'énoncé complet :

Soit f la fonction définie sur les réels par f(x)= (1/4)x² dans un repère orthonormé (O;I;J).

Soit A un point quelconque sur Cf et F le point de coordonnées (0;1). La droite (FA) recoupe Cf en B

Les tangentes en A et en B à Cf se coupent en I

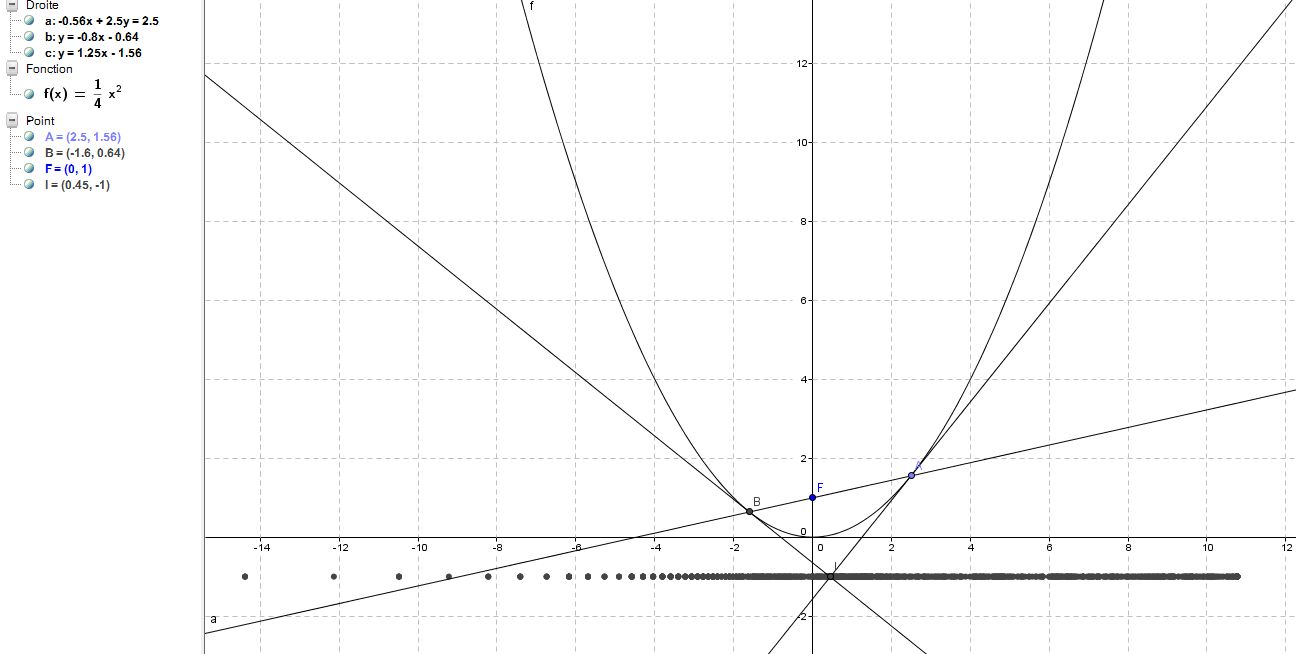
1. A l'aide de geogebra, construire une figure illustrant la situation.

voila ce que j'ai fais :

2. conjecturer la position relative des deux tangentes entre elles.
Les deux tangentes forment un angle droit.

3. Conjecturer le lieu géométrique du point I
Le point I a toujours pour ordonnée -1.

4.a. Exprimer les coordonnées de A en fonction de a.
A(a; f(a))
b. Déterminer l'équation réduite de (FA). c'est la que je bloque
j'ai essayer de trouver le coefficient directeur mais je me retrouve avec l'expression ((1/4)a² -1)/a , je ne sais pas comment aller plus loin

c. Déterminer les coordonnées de B.
d. En déduire les équations des deux tangentes.
e. Déterminer les coordonnées de I et conclure

Voila en espérant trouver de l'aide et en vous remerciant d'avance
-----

[invite51d17075]

je ne sais pas ce qu'on entend par équation réduite.?
tout ce l'on sait c'est que (a,f(a)) est à la fois sur la parabole et en même temps sur une droite passant par F.

[invite3ec2ccd8]

équation du type y=ax+b

[invite3ec2ccd8]

Personne ?

[A voir en vidéo sur Futura]

[invite8241b23e]

L'équation réduite est du type : y = ax + b, et non, ax + by + c = 0

[invite3ec2ccd8]

je sais bien mais il faut bien calculer a...

[invite51d17075]

non , on te demande f(a) en fonction de a , pas de calculer dans un premier temps a !

[invite3ec2ccd8]

Je vois pas du tout.. on m'a demandé les coordonnées de A en fonction dea ce que j'ai fais puis on me demande l'équation, sachant qu'on connait b je me suis dis qu'il manquait a et donc le coefficient directeur..

[invite51d17075]

excuses moi , je n'avais lu ça
"Les deux tangentes forment un angle droit."
donc le triangle est rectangle, ce qui donne une équation de plus.

[invite3ec2ccd8]

c'est après qu'on me demande les équations des tangentes mais la j'ai essayé de faire la dérivée U(x)/V(x) et j'obtient 1/2 mais c'est bizarre puisque la droit est croissante ou décroissante en fonction de a donc je peux pas avoir un coefficient forcément positif....

[invite3ec2ccd8]

je ne vois vraiment pas comment faire ...

[invite51d17075]

il me semble que tu te compliques un peu la vie
f(a)=(1/4)a²
f(b)=(1/4)b²
ensuite les points BFA sont alignés
et les tangentes forment un triangle rectangle.

[invite3ec2ccd8]

désolé mais je ne vois pas en quoi cela me permet de calculer le coeff directeur..

[invite51d17075]

les deux vecteurs directeurs des tangentes forment un angle à 90 °
donc le produit scalaire est nul.

[invite3ec2ccd8]

je n'ai pas vu les produit scalaire, que cela signifie ? pouvez vous développer la démarche car je suis vraiment largué la...

[invite8241b23e]

Si deux droites sont perpendiculaires, alors le produit de leurs coefficients directeur est égal à -1.

[invite3ec2ccd8]

et donc ensuite comment fait-on pour retrouver le coefficient de chaque tangente ?
je ne sais toujours pas comment retrouver celui de (FA)..

[invite51d17075]

reprenons dans l'ordre des questions, c'est plus simple je crois.
as tu déterminé les coord de B ?

[invite51d17075]

désolé, pas vu la page 2
messages croisés.

[invite3ec2ccd8]

je suis toujours bloqué a la question b. :/

[invite51d17075]

je ne sais pas ou plus ( à mon age ) ce que tu appelles "équation réduite" !
pour moi le point A est à la fois sur la parabole et sur une droite passant par F.
et toute tangente à la parabole coupe l'axe des x.
ou alors l'équation dite "réduite" fait intervenir le x ?
j'ai un pb de définition pour aller plus loin

[invite3ec2ccd8]

j'ai répondu plus haut que l'équation réduite correspond simplement a une équation de la forme y=ax+b ^^

[invite51d17075]

OK, donc la pente de ta tangente est 1/2
donc si
alors le se situe sur la droite
donc

[invite3ec2ccd8]

cependant je suis pas sur que 1/2 soit la bonne réponse

[invite3ec2ccd8]

et les coordonnées de I sont I(xi;-1)

[invite51d17075]

oui deux erreurs
la pente est de
et je n'avais pas vu que I avait pour ordonnée -1....
désolé.

[invite51d17075]

donc la tangente a pour équation

et d'ou


mais ça ne répond pas à ta question. y=ax+b ( enfin pas directement ) si on n'en sait pas plus sur A.
je cois que je suis crevé (medocs lourds )
j'y reviens tout à l'heure ou demain.

[invite3ec2ccd8]

Donc si le coeff est de (1/2)xa , sachant que l'ordonnée à l'origine est 1 on a y= ((1/2)xa)x + 1 ?

[invite3ec2ccd8]

il semblerai que le coeff soit bien ((1/4)a² -1)/a comme je l'avais dis plus haut, je me suis embrouiller en essayant d'aller plus loin..

[invite51d17075]

je crois avoir compris mon malentendu .
FA semble désigner la tangente qui a donc pour équation y=ax+b
et on connait un point et la pente.
la pente vaut bien (1/2)a
donc y=(1/2)ax+b
par ailleurs
pour x=a y=(1/4)a²
donc (1/4)a²=(1/2)a²+b, d'ou b
l'equation de la tangente en A est donc
y=(1/2)ax-(1/4)a²