Démonstration de géométrie

[inviteceaa4eb0]

Bonjour,

J'ai vu la démonstration de la propriété suivante :

Si un quadrilatère convexe possède au moins deux angles opposés supplémentaires, alors il est inscriptible dans un cercle.

Je me demandais si la réciproque Si un quadrilatère convexe est inscriptible dans un cercle, alors ses angles opposés sont supplémentaires. est vraie elle aussi.


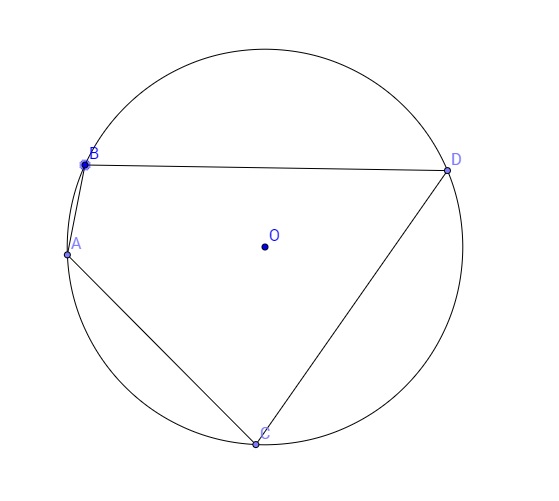
Figure d'étude :






Démonstration :


Soit un quadrilatère convexe ABDC de centre O.

Comparons les angles et

L'angle est un angle inscrit dont l'angle au centre correspondant est l'angle extérieur

L'angle est un angle inscrit dont l'angle au centre correspondant est l'angle intérieur


Propriété : Un angle inscrit vaut la moitié de son angle au centre correspondant.

Donc,

Angle extérieur = 2

Angle intérieur = 2


Donc :

Angle intérieur + Angle extérieur = 2 + )

Or,

Angle intérieur + Angle extérieur = 360°

Donc,

360° = 2( + )

Donc,

180° = +


Les angles et sont donc bien supplémentaires.


Merci à qui me lira ou répondra (le ou inclusif du coup )

Très cordialement,

Guillaume
-----

[gg0]

Bonjour.

Théorème de l'angle inscrit.

Cordialement.

[inviteceaa4eb0]

Bonsoir,

Je te remercie, en fait j'avais mal lu, ce théorème était bien dans le livre mais formulé très différemment.

Cordialement,

Guillaume

[invitea3531dcc]

Bonjour Guillaume_63 et bonjour à tous,

Aurais-tu un lien vers la démonstration de

Si un quadrilatère convexe possède au moins deux angles opposés supplémentaires, alors il est inscriptible dans un cercle.

Merci beaucoup pour votre réponse!

[A voir en vidéo sur Futura]