Dm de maths - Fonctions et dérivées

[invitee9dfaa77]

Bonjour à tous, je souhaiterais de l'aide pour mon DM de maths.

Voici le sujet :
On veut fabriquer une cuve à ciel ouvert, pouvant recueillir de l'eau. Cette cuve a la forme d'un pavé droit à base carrér de côté x en mètres, avec x appartient [1;6]. Elle a un volume de 4m³.

1. On note l la hauteur de la cuve. Justifier l'égalité l = 4/x²
Pour cette question, j'ai noté :
V = Longueur x largeur x l
donc
l = V/(Longueur x largeur)
l = 4/x²

2. On note S(x) l'aire en m2 de la surface à peindre. Démontrer que S(x) = x² + (16/x)
Je n'arrive pas à parvenir à bout de cette question...

3. Calculer S'(x)
Facile.
S(x) = x² + (16/x)
S'(x) = 2x - (16/x²)

4. Montrer que S'(x) = (2(x-2)(x²+2x+4))/x²
J'ai également réussi.
S'(x) = ((2x-4)(x²+2x+4))/x²
S'(x) = (2x3+4x²+8x-4x²-8x-16)/x²
S'(x) = (2x3-16)/x²
S'(x) = 2x - (16/x²)

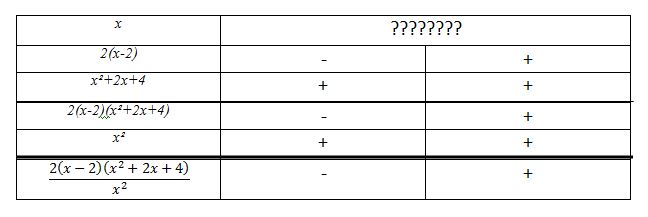
5. Dresser le tableau de variations de la fonction S.
Je ne comprends pas comment faire.

6. Quelles sont les dimensions de la cuve qui permettent d'utiliser le moins de peinture possible?
Pour pouvoir répondre à cette question, il me faut la réponse à la 5ème. Par conséquent, je ne peux pas trouver.

Merci beaucoup d'avance pour votre aide.
-----

[gg0]

Bonjour.

2) Fais un dessin. Tu sais calculer les aires des rectangles depuis des années.
5) Étudie le signe de la dérivée.

[invitee9dfaa77]

J'ai enfin trouvé la question 2.
Cependant, pour la question 5, j'ai essayé d'étudier le signe de la dérivée mais je n'y parviens pas. Je ne sais pas faire avec une telle fonction.
Je suis bloqué, je n'y arrive pas et ça m'énerve.

[gg0]

Tu as une factorisation de S' à la question précédente. A ton avis pourquoi ?
C'est en seconde qu'on voit les tableaux de signe, et en première le signe d'un trinôme du second degré.

[A voir en vidéo sur Futura]

[invitee9dfaa77]

Est-ce que c'est ça?
Par contre je ne sais pas quoi mettre dans la ligne "x"

[gg0]

Si tu ne sais pas, comment as-tu rempli les lignes ?????

Rappel : x varie de 1 à 6.