Flocon de Van Koch - Aire

[Melissa77]

Bonjour,
Je m'appelle Melissa et je suis en classe de 1ere L,j'ai été malade pendant une semaine et pendant cette semaine le prof de maths nous a donner un petit exercice à faire,mais je ne comprends absolument rien!
Voici l'intitulé :

Calculer l'aire du flocon:
Indications: pour n>1; An l'aire obtenue à l'itération n, on a Sn=Sn-1+An avec A0=S0

1. Calculer les deux premiers terme de A puis determiner An+1 en fonction de An
2. Déduire la nature de la suite (An) et préciser son terme et sa raison
3.Montrer que Sn = √3/4 + 3√3/20 (1-(4/9)n)

Pouvez vous m'aider ?
-----

[PlaneteF]

Bonjour,

Pouvez vous m'aider ?

Si tu ne mets pas le dessin qui doit normalement aller avec, ça va être compliqué de t'aider !

Cordialement

[HugoD]

Bonjour Mélissa,

Pour réussir cet exercice, il faut commencer par faire quelques petites recherches. Si tu es capable de te rendre sur Futura-Science, tu devrais être capable de chercher ce qu'est le flocon de Van Koch sur internet.
A vrai dire, ton exercice ne me semble pas complet. Il ne semble pas réalisable dit ainsi. Il faut nécessairement nous donner chaque information une à une pour obtenir des réponses qui t'aideront.

Qu'est ce que le flocon de Van Koch ?

Voici une image du flocon de Van Koch :



L'idée est de partir d'un triangle équilatéral de côté 1, et de faire un triangle plus petit à chaque côté du triangle. Pour cela, à chaque étape, on divise chaque côté en trois segments égaux et, en prenant pour base le segment du
milieu, on construit un triangle équilatéral à l’extérieur de la figure précédente.

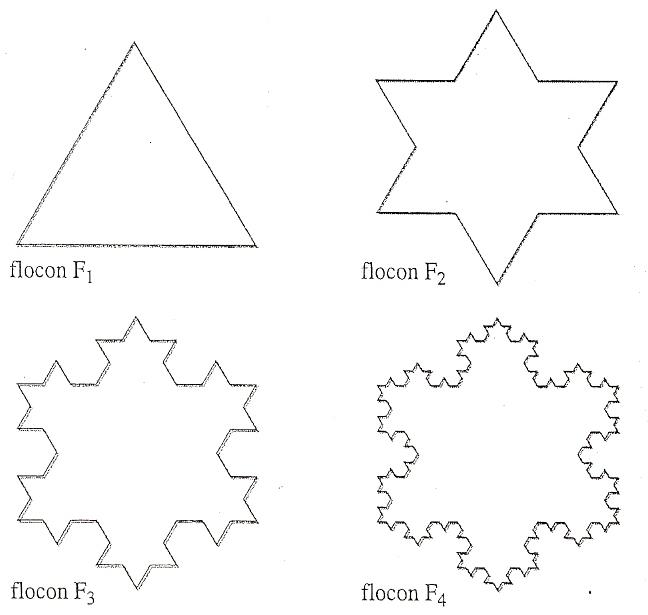
Peu à peu, on obtient une illustration d'un flocon de neige. Le flocon correspond à l'étape tandis que le flocon correspond à l'étape .

Ce que l'on appelle le flocon de Van Koch est le flocon obtenu lorsque tend vers l'infini ().

Qu'est ce que c'est que toutes ces suites et lettres ?

Nous savons donc ce que représente : c'est le nombre d'étapes du flocon.
représente l'aire du flocon pour un nombre d'étapes , c'est indiqué dans l'énoncé.

Et ?

Un petit début...

Voila quelques docs qui pourraient t'intéresser : http://maths-au-quotidien.fr/lycee/TP/flocon.pdf
http://villemin.gerard.free.fr/Wwwgv...e/FracAire.htm

Soit l'aire d'un triangle équilatéral :

Donc (rien du tout --> pas d'aire) et
(triangle équilatéral)


Honnêtement, sans plus d'informations de ta part, je ne peux rien te dire de plus :/

[Melissa77]

Merci de vos réponse rapide;
Juste avant j'ai eu à calculer le Périmètre du flocon mais ça,ça ne m'a pas posé de problème, je bloque juste sur l'aire ;
Je vous ai donnée l'énoncé tel qui est marqué sut ma feuille (la partie du périmètre en moins) :/

[A voir en vidéo sur Futura]

[Melissa77]

Si je comprends bien il faut que je calcule A0 et A1, que je détermine ensuite An+1 en fonction de An et que je dise quel est la nature de (An)n>1 en précisant son premier terme.

Selon l'énoncé : Sn est l'aire de la figurine Fn et que Sn= Sn-1 + An (ici j'ai pas trop compris)

[HugoD]

Si je comprends bien il faut que je calcule A0 et A1, que je détermine ensuite An+1 en fonction de An et que je dise quel est la nature de (An)n>1 en précisant son premier terme.

En réalité, il faudra calculer et puisque dans les indications, il est noté que n>1 (au passage, c'est ">=" ou ">" ?). Sinon, c'est ça.

A mon avis, la suite sera géométrique, du moins elle ne sera pas arithmétique.

Selon l'énoncé : Sn est l'aire de la figurine Fn et que Sn= Sn-1 + An (ici j'ai pas trop compris)

Et qu'est-ce que Fn ? Serait-ce la figure du flocon ?

Je pense que Sn est l'aire totale de la figure, et que An est l'aire du nouvel élément (nouveaux triangles).
Dans ce cas, tout s'explique. On comprend donc que Sn= Sn-1 + An.

Peux-tu faire une photo de l'énoncé, sinon nous n'allons pas beaucoup avancer... :/

[Melissa77]

La qualité de la photo n'est pas super super :/
En effet, n>=1 j'avais pas fais attention ^^
Et Fn est la figure du flocon

[Melissa77]

Donc on a A0 = S0 = 0 et A1= 1^2x√3/4 = √3/4
Pour " Déterminer An+1 en fct de An " je vois pas trop comment faire :/

[Melissa77]

J'ai : An+1 = an + kn x (cn+1)^2√3/4 car pour avoir l'aire suivante il faut l'aire précédente + l'aire des " petits triangles " notés kn
C'est potable?

[Melissa77]

Il faut que je montre par récurrence que Sn= A0 + A1 + ... + An
Comment faire?

[HugoD]

Re-bonjour Melissa,

Excuse moi de te répondre en retard, j'étais en voyage. Sur le chemin du retour, voila ce que j'ai rapidement écrit : http://img15.hostingpics.net/pics/93...0927141041.jpg
A toi de comprendre, de mettre en forme, et de répondre correctement aux questions à partir de ça. Crois-moi, ce n'est pas en répondant ce que j'ai écris que tu auras les points.

Concernant , il s'agit d'une question de cours. Si la suite est géométrique, alors . A toi d'appliquer tout cela, j'en ai assez dis !