Salut tous le monde ,
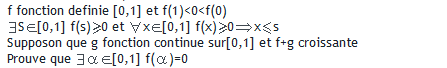
merci de voir la capture jointe
pour résoudre cet exercice il faut prouver que f est continue je pense la chose que j'ai pa pu trouver
Merci d'avance
-----


Salut tous le monde ,
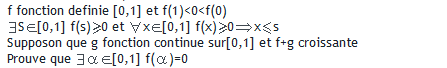
merci de voir la capture jointe
pour résoudre cet exercice il faut prouver que f est continue je pense la chose que j'ai pa pu trouver
Merci d'avance

Bonjour.
A ta place j'essaierais je prouver que le x donné dans les hypothèses est justement alpha. Sans chercher à justifier la continuité de f (*). par exemple en supposant (preuve par l'absurde) que f(x)>0 et utilisant la croissance de f+g et la continuité de g.
Cordialement.
(*) il est facile de trouver des exemples de fonctions f discontinues qui conviennent. avec des discontinuités "croissantes".


salut,
j'ai essaye avec ce que vous avez suggesse mais je me bolque a chaque fois

je le dirai autrement,
on peut montrer que si f est discontinue en un point , elle ne peut y être que croissante, sinon f+g ne l'est pas.
à la relecture, je répète un peu gg0.....


mais ca nous donne que f croissante et ca va pas nous aider a montrer que il existe un alpha


desole mais j'arrive pas a comprendre


Non.
Considère la fonction f définie par
si x<0.2 f(x)=x
si 0.2<=x<=1 f(x)=1-2x
Elle est discontinue (en 0,2), pas croissante, mais si tu prends g(x) = 3x, alors f+g est bien croissante (elle vaut 4x sur [0;0,2[ et x+1 sur [0,2;1].


Bonjour,
Merci gg0
je veux a chaque fois écrire ce que j'ai essaye mais j'arrive pas parce que ya pas de matrice .
Alors premièrement, en démontrant la discontinuité de la fonction f en un point ce point sera S je pense pour conclure que il existe le nombre 0 dans le groupe d'arrivé (f(Df))

Ton message ne répond pas à ce que nous t'avons dit, Ansset et moi. Et n'importe comment, tu te contentes de parler dans ces messages (le seul qui contient des maths est le premier).
Je ne comprends pas ton allusion à des matrices, ça n'a aucun rapport avec ta question.
Si un jour tu as vraiment envie de faire cet exercice, tu liras sérieusement nos réponses, puis tu te mettras au travail. Et si tu bloques, tu présenteras ce que tu as fait. on pourra voir. mais inutile de baratiner sur ce que tu dis avoir fait.

il me semble qu'un raisonnement par l'absurde peut aider.
Cdt


désolé ,j'ai rien compris de ce que vous avez dit,

une autre piste consiste à montrer que f a forcement un intervalle de continuité.
je te laisse avancer.


en prouvant que f(x) est continu j'ai 0<f(x)-f(s)<f+g(x)-f+g(s)
et ca nous donne que limf(x)-f(s)=0 alors la limf(a)=f(s)
on repete les memes etapes a gauche de a

Mais f n'est pas continue. Voir mon message #8


mais la discontinueté va pas nous aider ce que j'essaye de prouver moi que f est continue + decroissante===et ce nous donne quill existe un alpha qu'il appartient a Df et f(alpha)=0

Depuis le début on te dit que ça ne marche pas. Rien ne permet de prouver que f est continue, puisqu'elle peut être discontinue.
Depuis le début, tu parles seul, sans lire ce qu'on t'écrit. Inutile de continuer.
"je ne comprends pas" ! Bien sûr, tu ne cherches pas à comprendre, tu veux faire ce que tu as envie de faire, et ce n'est pas possible, mais tu veux quand même et tu ne lis pas ce qui montre que c'est impossible ...car ça t'obligerait à changer d'idée.

serait-ce mes propos qui ont été mal interprétés.?
j'ai juste dit qu'en un point ou f serait discontinue, alors f serait croissante en ce point.
car f+g est croissante et g est continue.
mais globalement on a f(1)<0<f(0)
donc f ne peut être discontinue partout.

je me rend compte qu'il s'agit d'un exercice de lycée.
tel qu'il est posté.
pas évident tout de même à ce niveau.

