Géométrie dans l'espace TS

[imprejo]

Bonjour, voilà un exercice de maths qui me pose problème :
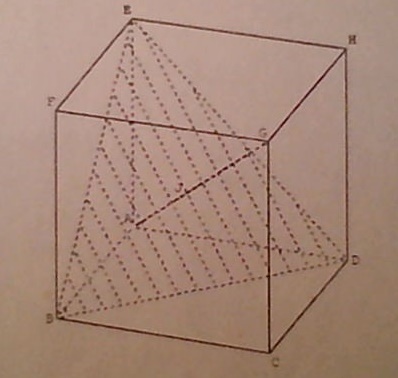
Soit un cube ci-contre

Trouver la position de J sur le segment [AG] pour que B,D,E et J soient coplanaires.
On pourra utiliser le repère (A;AB(vecteur),AD(vect),AE(vec t))

Voilà ce que j'ai pensé faire :
Coordonnées des points : B(1;0;0) D(0;1;0) E(0;0;1)
Coordonnées des vecteurs : BE(vect)(-1;0;1) BD(vect)(-1;1;0) BJ(vect)(xJ-1;yJ;zJ)

Existe-t-il des nombres x et y tels que : BJ=xBE+yBD ?
Sur AB --> xJ-1=-x-y
Sur AD --> yJ=y
Sur AE --> zJ=x

Mais il y a trop d'inconnues pour que je puisse résoudre ce système... Il faudrait peut-être utilisé la phrase de l'énoncé qui dit que J est sur le segment [AG] ?
Pourriez-vous m'éclairer ?
Merci d'avance
-----

[G.Renault]

Bonjour,

Ton idée est intéressante.
Effectivement, tu peux traduire le fait que J est sur le segment [AG]. C'est vrai à quel condition sur les vecteurs AJ et AG ? Cette condition t'éclairera fortement sur l'allure des coordonnées de J.

[imprejo]

Bonjour,

Merci pour votre réponse

Alors AJ(xJ;yJ;zJ) et AJ=kAG
Donc xJ=k*1
yJ=k*1
zJ=k*1
Je peux alors remplacer xJ,yJ et zJ par k dans mon système ?

Mais je ne trouverai toujours pas de valeur pour les coordonnées de J non ?

Merci

[G.Renault]

Oui, avec 0<=k<=1 pour être précis (J est sur le segment, pas sur la droite).

Je peux alors remplacer xJ,yJ et zJ par k dans mon système ?

Pourquoi pas ?

Mais je ne trouverai toujours pas de valeur pour les coordonnées de J non ?

Pourquoi pas ? Elles sont toutes égales à k, il te suffit de trouver la valeur de k.

[A voir en vidéo sur Futura]

[imprejo]

Ah oui ! Je n'avais pas eu l'idée de remplacer x et y par k dans la première équation de mon système final.
Merci pour votre aide