Bonjour, j'ai un DM de maths a rendre pour demain et je suis bloqué a la dernière question. Je dois prouver que les droites sont des tangentes de la courbe. Les données sont l'équation de la courbe : -1/3x²+2x et les équations des droites : (AC) y=2x (CB) y=-2x+12 (MN) y=(2-4t)x + 12t²
Merci d'avance pour votre aide !
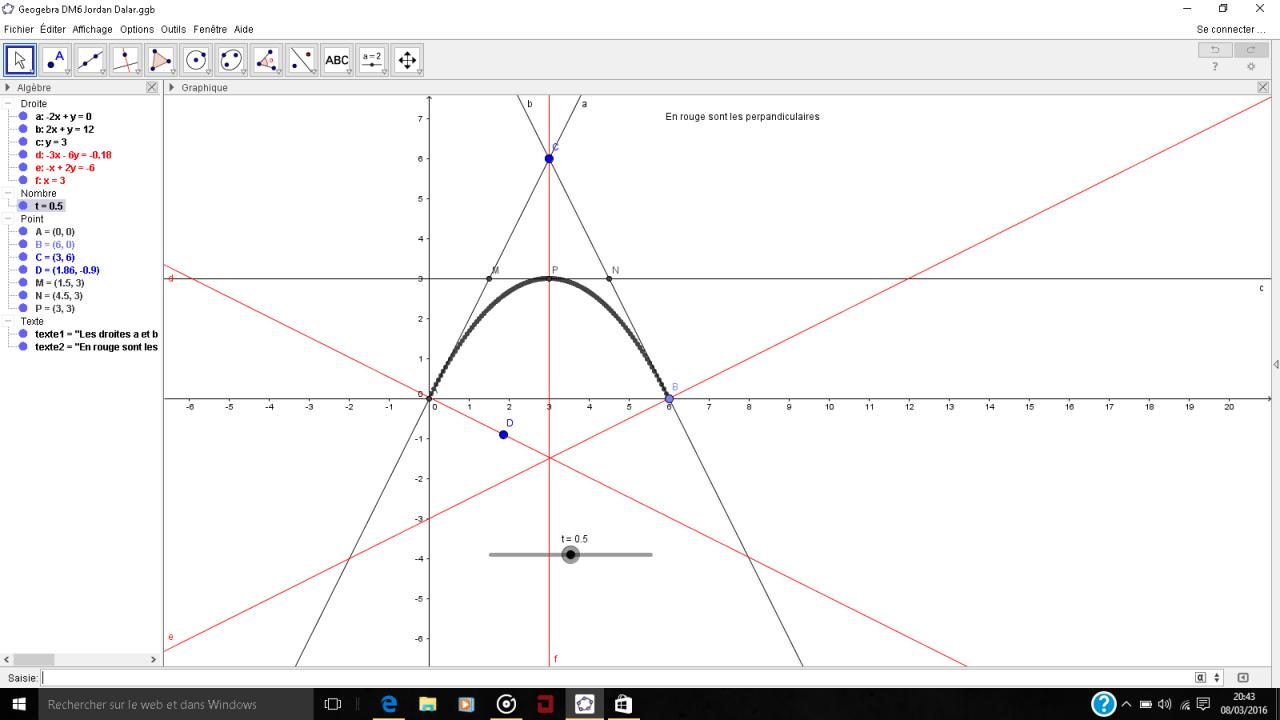[ATTACH=CONFI
voici la courbe et les droites en question
Bonjour.
Sans l'énoncé précis, difficile de faire mieux que de te rappeler que la tangente coupe la courbe et que son coefficient directeur en ce point est la valeur de la dérivée.
C'est quoi, ce t dans l'équation de (MN) ?
Cordialement.
Dernière modification par gg0 ; 08/03/2016 à 20h51.
Bonsoir, concernant l'énoncé, nous devions conjecturer dans un premier temps que ces droites étaient des tangentes a la courbe, puis maintenant nous devons le démontrer.
Concernant le "t", c'est la variance comme vous pouvez le voir la photo. Lorsqu'on varie "t", la droite (MN) change, elle varie en fonction de "t" (d'où le t dans l'équation de (MN))
Cordialement.
Eh bien, tu as ta méthode, si tu as vu les dérivées (il y a une autre méthode basée sur l'idée de racine double).
NB : Pour l'instant, je ne peux pas lire ton document ("Pièces jointes en attente de validation").
En fait je sais qu'il faut que je calcule f'(a)(x-a)+f(a) sauf que ça je ne sais pas le faire et quand même je l'aurais calculé je ne sais pas l'interpréter
Pourquoi sauter tout de suite sur une formule au lieu de réfléchir à la situation en apprenant tes leçons. D'autant que je t'ai donné la méthode, il ne te reste qu'à l'appliquer.
Serais-tu en train de demander qu'on fasse ton travail ? Lis http://forums.futura-sciences.com/ma...ces-forum.html.
D'accord. Donc reprenons : j'ai le coefficient directeur de la tangente (2) donc j'ai la dérivé. Ensuite que faire avec cette dérivé ?
Prenons l'exemple de la première droite :
Où coupe-t-elle la courbe ? quelle est l'abscisse de ce point ? Combien vaut la dérivée pour cette abscisse ? Est-ce le coefficient directeur de la droite ?
Sérieusement, à partir de la définition de la tangente en un point à une courbe et de l'interprétation géométrique du nombre dérivé, tu pouvais te poser ces questions et y répondre seul, non ?
Rappel : Ton prof de maths et moi même ne faisons rien d'autre que d'utiliser intelligemment les règles du cours. Comme tu es à priori aussi intelligent (peut-être même plus vu ton âge et la fraîcheur de ton cerveau), tu peux le faire !
Cordialement.
