coucou tout le monde!
Voilà à peine rendu et déjà un nouveau DM et donc déjà des problèmes!
je vous note l'énnocé ,ce que j'ai déjà su faire et ce qui me bloque alors,
Le plan est rapporté a un repère orthonormal (o;i;j)
la courbe représente la fonction f définie pas f(x)=sin²x
x étant élément de l'intervalle [0;'pi'].le domaine D est l'ensemble des points M(x;y) du plan, tels que 0<x<pi et
0<y<f(x)
1.calculer l'aire du domaine D en cm² pour cette question j'ai un schéma mais je en peux pas le faire!
Je bloque un peu pour cette question j'ai calculer l'intégale entre 0 et pi de sin²x dx
jobtient donc [-cos²x]en 0 et pi
mais mon probléme c qd simplifiant cela je trouve 0!
2.Linéariser sin^4 x et en déduire intégrale entre 0 et pi sin^4 x dx
Pour celle ci je pense m'en étre sortie j'ai utilisé la méthode d'euler et apré plusieurs calculs je trouve
(1/32)sin4x-(1/4)sin2x+(3x/8) qui est dc une primitive de x qui donne sin^4(x)
3.a.Le nombre x étant élément de l'intervalle [0;'pi'] on considère les points A et B d'abscisses x, B appartenant a la courbe C.Le segment [AB] pivotant autour de l'axe (o;i) engendre un disque dans l'espace.Exprimer l'aire en cm² de ce disque en fonction de x.
Voila et c la que sa ce complique pour moi!! lol je voulais mettre qur l'aire d'un disqu était 'pi'R² et que comme A et B st 2points d'abscisses x alors[AB] est le rayon du disque d'ou A='pi'R²
mais je pense que c tp rapide dc ça ne peut etre bon.non?
et enfin 3.b.En déduire le volume en cm cube du solide obtenu par la rotaion de a courbe C autour de l'axe des abscisses.
voila et donc la ça bloque carrèment je ne vois pas comment faire...
merci d'avance pour toutes réponses!!
-----





 , ce n'est pas
, ce n'est pas 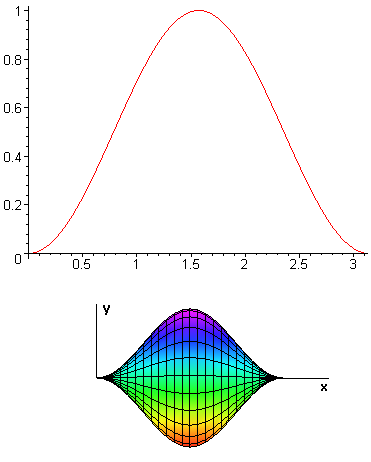
 sin 4pi= pi/2 ???
sin 4pi= pi/2 ???

