Calcul de la somme des longueurs de corde sur une surface

[invite8e757dd6]

Bonjour

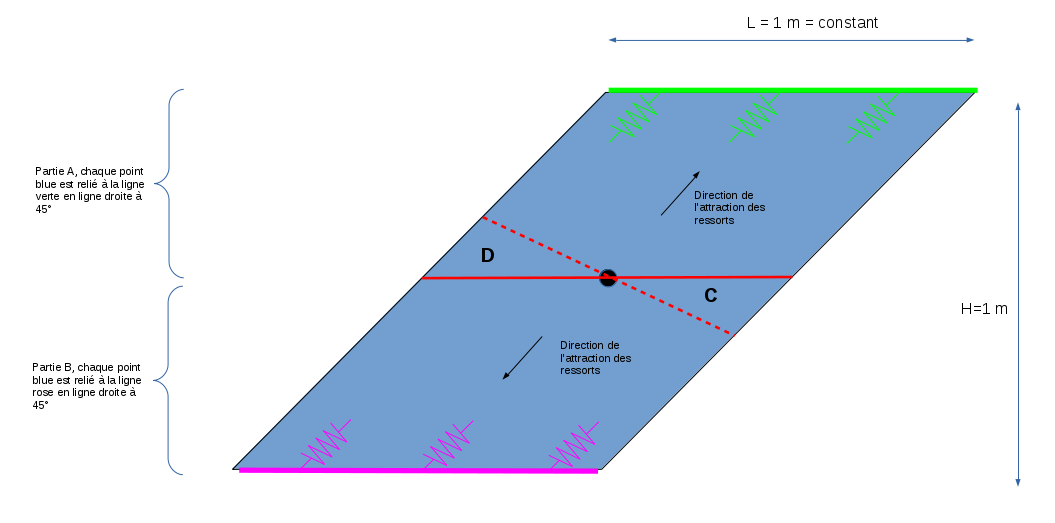
J'ai un parrélogramme qui est comme ceci au départ:

dx12.png

Au final, il est comme cela:

dx13.png

La surface reste constante. Mais la ligne qui sépare les deux parties va tourner sur elle-même et une partie des points bleus doivent se déplacer de proche en proche. Chaque corde est fixé sur la ligne verte ou rose.

Je regarde les longueurs entre la ligne verte et chaque point bleu de la partie A et leur évolution sachant que les cordes sont fixées sur le ligne verte. Idem pour la partie B. Au départ les cordes sont à 45° mais ensuite ce n'est plus le cas car les cordes sont fixées sur le ligne (verte ou rose) et ensuite comme les points bleus doivent se déplacer chaque corde fait un angle différent.

Je souhaite savoir si les longueur au final sont plus grandes qu'au départ.

Pour moi, c'est évident que c'est plus long au final, mais je n'en suis pas certain, et je ne sais pas comment faire le calcul.

Merci par avance
-----

[gg0]

Bonjour.

Ton énoncé est loin d'être complet : On ne sait ni combien il y a de cordes, ni où elles sont fixées. Et on peut espérer que tes cordes sont élastiques, pour qu'il y ait la possibilité de bouger.

A toi d'expliquer mieux !

[invite8e757dd6]

Ok, désolé. Je sais pas si on peut partir sur une infinité de points bleus en mathématique, sinon comme l'aire fait 1m², disons un point tous les 1µm². Oui, les cordes sont élastiques, elles sont fixées à un bout à la ligne verte (ou rose) mais l'autre bout qui est fixé à un point bleu peut bouger librement. Peut être qu'il y a plusieurs possibilités mais je souhaite comparer avec la longueur minimale au final. A la limite, peut être que pour avoir le chemin, il est souhaite de considérer que chaque corde attire pour voir comment se placent les points bleus mais là ce serait plus de la physique. Si c'est possible je préfère traiter cela en maths.

Merci

[invitef29758b5]

Salut
Il n' y a pas de liaison entre les points bleus et la ligne rouge .
Donc aucune raison pour que les points bleus se déplacent .

[A voir en vidéo sur Futura]

[invite8e757dd6]

C'est un calcul de longueur, peu importe ce qui fait bouger les points. J'ai des longueurs de cordes au départ, je les bouge et je regarde la somme des longueurs au final. Au départ chaque corde fait 45° mais ensuite, je ne sais pas, peut être que peu importe la disposition (angle des cordes) la somme des longueurs au finale est peut être toujours la même, cela fait partie de la question.

[invitef29758b5]

C'est un calcul de longueur, peu importe ce qui fait bouger les points.

Ce qui fait bouger les points détermine comment ils bougent .
Sans cette information , on est comme toi :

je ne sais pas

On ne saurait mieux dire .

[invite8e757dd6]

1/ Peut être que la somme des distances ne dépend pas du placement ?
2/ Est il possible de trouver le placement minimal pour chaque point bleu pour avoir la somme des distances minimale ?
3/ Si la réponse est non à 1/ et 2/, si je pars sur un problème de physique, chaque corde attire comme un ressort, la contrainte est elle suffisante ?

[gg0]

1) La somme des distances dépend du placement. Essaie avec 2 cordes, en les plaçant de façons différentes
2) Dans quel cas ?
3) Si c'est un autre problème, il faut le poser correctement.

Deux remarques :
* Les aires restent égales, donc si les cordes sont régulièrement disposées elles ne changent approximativement pas de longueur totale, et même pas du tout si elles sont disposées symétriquement par rapport au centre du parallélogramme
* Les points bleus sur le dessin ne sont pas sur la sécante, ce qui rend l'interprétation assez aléatoire (on peut se tromper, puisque le bleu est l'intérieur du parallélogramme).

[invite8e757dd6]

"1) La somme des distances dépend du placement. Essaie avec 2 cordes, en les plaçant de façons différentes" oui pour 2 cordes mais si je prends les distances max ensuite je n'ai plus ces places de disponible et je me disais que peut être quand on fait la somme de tous les points alors ce serait pareil, mais c'est juste une idée
2) Dans tous les cas, à partir du fait que les cordes sont toutes au départ à 45° et dont un bout est attaché sur la ligne verte (ou rose). C'est compliqué (pour moi) puisque c'est de la recherche opérationnelle, c'est trouver la somme minimale des longueurs pour tous les cas possibles.
3) Ce n'est pas un autre problème, c'était pour répondre à Dynamix, il dit qu'il faut savoir ce qui va obliger les points à bouger ce qui est utile si les maths ne peuvent résoudre le cas 2). Dans ce cas, chaque corde est un élastique qui attire avec la même force chaque point bleu. Les cordes sont à 45° au départ et un point de chaque corde est fixé sur la ligne verte (ou rose). Ensuite, je tourne dans le sens horaire en forçant la barre centrale rouge au centre noir et je force ainsi les points bleus à se répartir autrement. Est ce que c'est assez explicite ? Je pense que les points bleus bougent de proche en proche.



"* Les points bleus sur le dessin ne sont pas sur la sécante, ce qui rend l'interprétation assez aléatoire (on peut se tromper, puisque le bleu est l'intérieur du parallélogramme). " je ne comprends pas, si vous pouvez m'en dire plus ?

[gg0]

Donc "les points bleus" sont bien ceux qu'on voit en bleu sur les dessins du message # 1 ? Dans ce cas, soit il y en a une infinité, et la question n'a pas de sens, soit ils sont en nombre fini, et si on ne connaît pas leur placement, la question n'a aucun sens.

Ce fil est en train de partir en quenouille !

Bon, si tu as un énoncé sérieux, on pourra voir ...

[invite8e757dd6]

Oui, la zone bleue sont là où se trouvent les points bleus. Et soit mathématiquement on peut partir sur un nombre infini de points soit par exemple on dit un point c'est 1µm² sur une surface de 1m² ça ira bien, c'est un cas réel.
Merci

[gg0]

Pour un nombre infini de points, la longueur totale est infinie (sauf si on prend des cordes de longueur nulle).

C'est toujours du n'importe quoi !

On dirait une tentative de traiter des problèmes de tension superficielle en les ramenant à de la tension filaire avec une modélisation délirante.

Le mieux serait quand même d'exposer le cas réel, qu'on sache ce qui se passe vraiment.

NB : marre des questions mal posées par des gens qui écrivent n'importe quoi comme traduction d'un problème concret.

[invite8e757dd6]

Rien de réel, juste une étude de longueurs, c'est vous qui pensez que c'est un problème concret. Comme je l'ai écrit 1m² de surface bleue et 1µm² de surface pour chaque point. Chaque point est attiré, je force la paroi rouge dans le sens horaire, les points vont bouger et se répartir au fur et à mesure de proche en proche comme le ferai des molécules d'eau. Un point=une molécule d'eau si vous voulez. Les cordes attirent comme la gravité peut le faire. Bon je voulais pas faire un exercice de physique si simple soit il parce ce que je pensais que la longueur finale était forcément plus grande à la fin et cela quelque soit le placement.

[gg0]

Si c'est un problème abstrait il est mal posé. Tu refuses depuis le début de le poser correctement, inutile de continuer, il n'y a pas de problème. Et après avoir dit "Rien de réel", tu écris "comme le ferai des molécules d'eau" tu te contredis. Sans oublier que " juste une étude de longueurs" alors que tu te refuses à dire lesquelles, tu es vraiment bizarre !!!
J'ai essayé de t'aider, mais je ne peux pas inventer ce que tu refuses de préciser.

[invite8e757dd6]

C'est abstrait oui, et j'ai donné un parallèle avec la physique pour répondre à Dynamix et à vous aussi. Je ne me contredis pas, je réponds à ce qu'on me demande. On me dis qu'il faut savoir comment les points bougent. Je réponds, chaque corde est un élastique qui attire comme la gravité par exemple, et c'est un exemple. L'étude des longueurs c'est la somme de toutes les longueurs des cordes, c'est pas compliqué à comprendre. Dans la zone bleue de 1m² il y a 1000000 point bleus par exemple, et c'est un exemple. Il y a un dessin au début, un dessin à la fin. Je veux savoir si la somme des longueurs finale est égale, inférieure ou supérieure à la somme des longueurs initiale. C'est une recherche de minima, cela peut se faire avec N points peu importe N, 1000000 si vous voulez. La comparaison peut se faire avec 10000 points ou 1000000 la comparaison donnera le même résultat. Par contre, c'est vrai, je suis bizarre.

[invite8e757dd6]

J'explique ce que je veux calculer avec ce premier exemple:



Un récipient contient de l'eau, il y a la gravité. La paroi du haut est en rotation autour du point noir. Il y a un couple sur la barre rouge, une partie de l'eau a descendre et l"autre va monter. Comme la gravité est verticale, si je mesure toutes les cordes verticales de chaque molécules d'eau entre la molécule et la paroi du bas, la somme des longueurs au départ est la même que la somme des longueurs au final.

Maintenant, c'est le même exemple mais sans la gravité, chaque molécule d'eau est attiré par une corde (virtuelle) à partir de la paroi du bas. Il y a un couple aussi sur la paroi rouge donc les "molécules" vont bouger et les longueurs des ressorts vont changer. Chaque ressort est attaché à la paroi du bas, donc au départ la corde est vertical mais ensuite elle ne l'est plus pour certaines, il y aura un angle entre la corde et la verticale. Une partie des ressorts va se réduire et une autre va s'allonger. Je souhaitais faire la somme de ces cordes. Et maintenant que j'ai vu qu'il y a un couple sur la barre rouge, on récupère une énergie et donc la somme des longueurs des ressorts doit forcément se réduire. Mais en dessinant comme cela je me demande vraiment si cela diminue car j'ai l'impression que les angles augmentent les distances mais un mathématicien doit voir cela rapidement.

Dites moi si c'est assez clair comme exemple ?

[invite8e757dd6]

Bonjour,

Si avec le dessin précédent, il est évident que les longueurs diminuent, je peux dire globalement que la partie en haut va prendre la place de la partie en bas et à part un problème d'angle qui va changer la pression sur la barre rouge, sur un petit angle au départ, le raisonnement est valable, c'est moins évident avec ceci :



La partie C "descend" (je dis descends dans le sens de l'attraction qui est oblique de 45°) mais la partie D "monte". Il y a un couple sur la barre rouge autour du point noir donc pour la conservation de l'énergie la somme des longeurs doit être différente au départ qu'à l'arrivée, elle doit être moins grande à l'arrivée. Hors ici, visiblement, je vois pas comment, sur un petit angle, les points bleus considérés comme des molécules d'eau qui se déplacement de proche en proche pourraient faire une somme moins grande.

C'est juste une intuition, des calculs sont nécessaires, si vous avez une idée de comment faire ou un lien ?

Merci

[invitef29758b5]

Un problème à la grouille sans boules , ce n' est pas un vrai problème à la grouille .
Si tu mets des boules à la place des points , celle qui sont en C sont chassées vers D
Les cordes vont s ' emberlificoter ...

[invite8e757dd6]

Oui de petites spheres donc une certaine taille. Oui, il va y avoir un déplacement peut être pas forcément tout ce qu'il y a de C vers D mais de proche en proche un déplacement des sphères je pense. Pour ce qui est de l'emberlification eh bien, j'imagine une seule couche de spheres bleues et les ressorts peuvent être dans des plans différents, c'est un peu théorique. Je crois que vous avez raison il faut savoir ce qui force les spheres à bouger mais ce doit être la même chose que les molécules d'eau font lors d'un déplacement d'une zone de pression à une autre. Ce qui est bizarre comparativement à la gravité c'est que les ressorts sous la zone C vont perdre une certaine longueur mais que la zone D va récupérer la même longueur et la somme des longueurs doit forcément être inférieure.

Merci