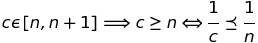bonjour, trois inégalités à montrer:
Pourrai je avoir une petite correction svp?
merci pour tte aide.
1),
2)que si a et b st deux réels non nuls distincts et de même signe :
3)
1)
alors
donc
2)
puisque,
donc,
3)
pour finir, comment faites vous pour montrer que cette somme* est inférieure ou égale à 1?
somme des termes d'une suite géométrique de raison 1/2
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
ah cool
c'est sympa ! je me penche sur cette suite.
merci,jacknicklaus
Bonsoir,
j'ai tenté de démontrer vôtre résultat,est ce comme ceci que vous avez procédé?
merci,d'avance
on pose ,
Il suffit de partir de l'identité
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Il suffit de partir de l'identité
Dès lors
Dernière modification par jacknicklaus ; 23/04/2017 à 22h20.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
bonsoir,
je ne savais pas que sa correspondait à ce type d'identité
Ce résultat déduis de mon dernier post n'est pas faux,juste lourd..
merci à vous
bonjour , j'ai une petite question comment vous pouvez écrire les notions mathématique avec votre clavier s'il vous plaît?
@skandertrifa
lire ici -> http://forums.futura-sciences.com/ma...res-forum.html
pour apprendre, un méthode simple est de faire "répondre avec citation" sur un message qui contient une formule qui t'intéresse, afin de récupérer par copié-collé le bout de code TEX qui correspond.
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
Pour le 1, c'est encore le TAF
Bonsoir,
je n'ai pas très bien compris le TAF qu'est ce que c'est?
Merci,
le TAF c'est le théorème des accroissements finis:
mais avec un ptit calcul, on s'en sort très bien
1)
on a
merci,
j ai fais comme vous par l'application du conjugué ,c 'est plus rapide en effet.je vais m’intéressé à ce théoreme
merci ansset
objectivement, je ne vois pas comment il l'utilise directement pour ça !?
Bonjour,
je tiens peut être un début d'explication suite à l'idée de joel
Prouvons:
1)
soit,
continue,sur son intervalle et dérivable sur
Bon après je ne sais pas trop si c'est toléré d'apporter des conditions? et puis est ce vraiment suffisant cette égalité?
A vous de juger,je partage vôtre avis
me reste à approfondir ce théorème intéressant
et on deduit le reste n'est ce pas?
.............................. ........
en fait, c'est une extension du théorème des valeurs intermédiaires pour les fct dérivables.Envoyé par fartassette
sinon, c'est à joel de nous dire comment il procède, je pense.
Bonsoir, skandertrifa
oui le point
Encore faut il que ce raisonnement soit juste, comme le dit Ansset ,à joel d'apporter la justification
bonne continuation,
Dernière modification par fartassette ; 25/04/2017 à 00h59.
oui le point
oui c'est bien ça.
on a
correct !
et c'est un théorème utile ( une extension du Théorème des Valeurs Intermédiaires )
mais , s'il n'a pas été vu en cours, c'est pédagogiquement une réponse "à coté".
que n'apprécierait aucun prof.
Bonsoir,
Oui,en général j’évite de surprendre le prof
Je cherche à évoluer dans cette discipline, apprendre des nouvelles notions car c'est franchement ennuyant en cours.J'ai hâte que l'année scolaire se termine
merci
