Calculs autour de l'aire d'un segment du disque.

[Jeryko]

Bonsoir à tous,

L'aire d'un segment de disque se calcule à l'aide de la formule suivante :
A = R² arc cos (h/R) - h racine² (R²-h²) c'est à dire l'aire du secteur arc de cercle moins l'aire du triangle.
où R = le rayon du cercle et h = distance centre du cercle à la corde.
Pas de problème, tout va bien.
Voir éventuellement : http://villemin.gerard.free.fr/GeomL...RE/Segment.htm

Je voudrais faire l'inverse :
Calculer h à partir de l'aire du segment de disque et de R.
Je n'y arrive pas.
Quelqu'un pour me donner la formule !
Merci
-----

[Dlzlogic]

Bonjour,
C'est un classique. Je ne connais pas d'autre méthode que un calcul approché. La méthode Newton est bien adaptée.
On rencontre en particulier ce cas dans le calcul de dimensionnement en assainissement.

[Jeryko]

Bonjour Dlzlogic,

Merci pour ta réponse, je pensais à une solution plus simple.

On rencontre en particulier ce cas dans le calcul de dimensionnement en assainissement.

exact : c'est mon cas.

J'ai regardé Wikipedia et d'autres sites sur le sujet.
Pour une équation simple du 2ème degré ou une racine carré ça va encore mais si je dois y ajouter de la trigo ....
Mes connaissances en math sont trop anciennes pour me replonger là dedans.
Dommage.

Ou alors il me faudrait un exemple ! (je n'ai pas trouvé)
Si quelqu'un passe par là ou me trouve un lien vers ce genre de problème ...
Merci à tous.

[gg0]

Bonjour Jeryko.

Tout dépend de tes besoins. Si tu n'as pas besoin d'une grande précision, tu peux approximer grossièrement R² arc cos (h/R) - h racine² (R²-h²) par Pi*R/2(R-h); ce qui donne h=R-2*A/(Pi*R). On peut avoir une meilleure approximation avec des fonctions affines par morceaux, ou de degré supérieur.
Si tu as besoin d'une bonne précision, et seulement de quelques valeurs, il suffit de calculer des valeurs approchées correspondantes (on peut utiliser une calculette ou un tableur); si tu as besoin d'une grande précision ou s'il s'agit d'un programme permettant de calculer pour n'importe quelle valeur, il va falloir utiliser des bibliothèques de calcul.

Cordialement.

[A voir en vidéo sur Futura]

[ansset]

l'idée de passer par une itération "à la newton" est bonne.
le principe est de trouver le 0 d'une courbe en partant d'un point de la courbe.
ici en reprenant ton calcul :
A = R² arc cos (h/R) - h racine² (R²-h²)
On peut la simplifier en prenant A1=A/R² et x=h/R.
A1=acos(x) -x*rac(1-x²)
On connaît A1 ( <= pi/2 ) et on cherche x ( 0<=x<=1)
soit
f(x)=acos(x) -x*rac(1-x²)-A1 et on cherche x tel que f(x)=0
l'algorithme revient à se rapprocher de la bonne valeur en utilisant la tangente à chaque itération.
en prenant un u0 qcq, u1 est donné par l'intersection de la tangente en (u0,f(u0)) avec l'axe des abscisses ( faire un dessin permet de visualiser )
la tangente de la courbe de f en u0 vaut
T0(u)=f(u0)+(u-u0)f'(u0)
T0(u1)=0 =>
u1=u0-f(u0)/f'(u0)
puis u2,u3....etc jusqu'à la précision voulue.
donc globalement on peut facilement itérer sur excel u(n+1) par rapport à un.

ps: ici f'(x)=-2*rac(1-x²)

ps : il faut évidement pour le test prendre A1 <= pi/2.
et pour l'initialisation , autant prendre par défaut u0=x=1/2

En espérant avoir été clair.

[Jeryko]

Bonsoir à tous,

j'ai trouvé une méthode basée sur des approximations successives (Newton)
à l'aide d'un tableur Excel que je ne peux transmettre directement.
Dans un 1er temps, je transmets une image et si cela intéresse quelqu'un je vais trouver une solution
pour transmettre le fichier Excel.

Est-ce la meilleure solution : j'en doute mais c'est mieux que rien !
J'espère qu'il n'y a pas d'erreur ?

Je vais étudier les autres propositions.
Merci à tous

[Dlzlogic]

Si vous nous donnez plus de détail sur la raison pour laquelle vous cherchez à faire ce calcul, on pourra peut-être vous guider un peu plus.
Le calcul de la hauteur d'eau dans un tuyau est un point mineur par rapport au problème réellement posé.

[ansset]

bjr,
intuitivement, je ne pense pas qu'il s'agisse d'un tuyau, mais plutôt d'une cuve cylindrique.
Cdt

ps: je n'ai pas regardé ton calcul ( *) , mais vu la nature de la courbe, la convergence est ici très rapide avec une récurrence à la newton.
(*)tu as pris des variables diff des miennes, et je ne vois pas clairement un calcul à la newton dans ce que tu fais. ( pas de dérivée de fct )

[ansset]

de fait je ne comprend pas:
- aire segment ( ce n'est pas 75% du total ? ici )
- ce qu'est "écart".
- pourquoi l'incrémentation en ecart/2
- pourquoi un cos(alpha/2)
- le tableau de vérif .

[ansset]

juste un pb de lecture et de compréhension, car je trouve le même résultat.

[Jeryko]

Bonjour à tous,

Je suis heureux de voir vos réactions et j'espère en savoir un peu plus sur le sujet que j'ai découvert.

- Je n'ai pas encore eu le temps d'étudier vos propositions ni de vérifier mes résultats en profondeur.
- Effectivement, il s'agit d'une cuve (que je considère parfaitement cylindrique) donc comme un tuyau.
- La convergence est très rapide sauf pour des remplissages au delà des 95% donc nombreuses itérations nécessaires.
- Aire segment ( ce n'est pas 75% du total ? ici ) - Réponse : ben si, 5026 * (100% -75%) = 1256 ? je ne comprends pas la Q.
- Ce qu'est "écart". - Réponse : c'est la différence entre le k recherché et k trouvé. (1,570796 - 1,090702 au démarrage)
- Pourquoi l'incrémentation en écart/2 - Réponse : ajout de la moitié de l'écart pour m'approcher de la valeur réelle.
- Pourquoi un cos(alpha/2). - Réponse : C'est l'application de la formule de base dans tous les cours.
exemple http://villemin.gerard.free.fr/GeomL...RE/Segment.htm
- Le tableau de vérif . - Réponse : Il s'agit de quelques tests rapides pour 2 valeurs complémentaires.
Nota : la 1ère valeur de a = 2 est empirique. d'autres valeurs ne changent rien.

@ansset : Tu trouves le même résultat. donc ce n'est pas trop mauvais ! Merci pour cette vérification confirmée qui me rassure.
A+

[ansset]

avec une "vraie" itéraction à la newton, tu converges très vite qcq soit le remplissage.

[ansset]

pour le reste, question de notation.
j'appelais remplissage la partie "remplie" , et ici tu prend la partie "vide".
donc , quand je dis "le même résultat", c'est en ayant interprété ton calcul.
sinon oublie l'histoire du alpha, question encore une fois de notation initiale.

sans dessin, parfois l'interprétation des inconnues n'est pas évidente.
Cdt

[Jeryko]

Re

Le fichier en téléchargement :

*** fichier sur serveur externe ***

@ansset : Je vais revoir le fichier pour tenir compte de tes observations.
Pour une "vraie" itération à la newton, je ne sais pas faire pour l'instant.

Merci.

[ansset]

Pour une "vraie" itération à la newton, je ne sais pas faire pour l'instant.
.

j'ai essayé de l'expliquer dans mon post #5.
tout à l'heure , je vais voir si je peux faire un petit dessin.
Cdt

[Jeryko]

Re bonjour,

Oui mais je n'ai pas encore eu le temps devoir cela en détail. Laisse-moi quelques jours.
Je suis retraité donc, toujours bousculé hi hi !. Tu verras ...

Au départ c'était un besoin pratique pour une cuve, ça devient un jeu de révisions.

Je ne sais pas si un petit dessin suffira ? Si tu pouvais me faire une feuille Excel ... ,

Bien à toi.

[ansset]

OK, mais le dessin serait très parlant, pour comprendre l'itération.
Et suis en panne d'encre à l'instant..... donc impossible de faire les manips prévues.
à tout à l'heure.

[Dlzlogic]

Bonjour,
Si c'est pour une cuve et non un tuyau, alors le but est de calculer à partir d'un volume. Or les extrémités d'une cuve cylindrique ont la forme de calotte sphérique. Cela agrémente le problème.

[Jeryko]

Bonjour à tous,

@Dlzlogic
"Cela agrémente le problème" Oui j'aime. Mais au départ je n'arrivais à rien.
J'ai donc simplifié en précisant : cuve supposée parfaitement cylindrique.
La précision mathématique n'était pas primordiale.

Pour info.
Mon lien sur le fichier Excel qui utilise des formules a été supprimé (message #14) Dommage.
J'ai posé la question aux modérateurs : comment faire autrement ?
- J'ai déjà transmis une image (jpg) de page Excel sur mon message #6
- Les MP ne permettent pas de joindre des fichiers me semble-t-il ?

Cordialement

[ansset]

pourquoi tu cherches à compliquer le sujet.
qui est présenté comme une cuve ( en partie remplie ) à bords ( extrémités ) supposés plat.
du fait la longueur de la cuve , on s'en fout dans le calcul cherché.

[Dlzlogic]

"pourquoi tu cherches à compliquer le sujet."
Je ne cherche pas à compliquer les choses, simplement à être plus rigoureux dans le raisonnement.
Soit on cherche une méthode la plus exacte possible, alors il ne faut faire aucune impasse, et avant de pouvoir dire "c'est négligeable" il faut l'avoir calculé. Soit on cherche une valeur approximative, alors une méthode graphique ou le calcul en partant de h ou toute autre méthode simplifiée convient.

[ansset]

je n'y suis pas opposé, on peut tout à fait faire un calcul plus complexe, mais on a pas les infos pour ça.
manquerait la forme des cotés ( semi-sphériques ?) et le rapport L/R ( Longueur sur Rayon ) de la cuve.
car si celui ci est grand , la forme des extrémités importe peu ou moins.

[ansset]

bonjour, je vais essayer de ré expliquer la méthode de newton.
On a une fonction f(x) ( assez régulière ) et on cherche x tel que f(x)=0

prenons ici ton calcul de surface :
A = R² arc cos (h/R) - h racine² (R²-h²)
formule que je simplifie en prenant x=h/R , elle devient.

On connaît A donc A/R² et on cherche x.

ps: ici je me place pour simplifier avec x entre 0 et 1 donc entre une citerne demi pleine ou vide. ( soit donc A/R² <= pi/2 )
(dans l'autre cas, on peut faire le calcul inverse qui consiste à prendre x pour la partie encore vide de la citerne )
mais l'idée est de présenté le principe du calcul.
soit

cette fonction est décroissante avec une dérivée

le principe général est de partir d'un point de la courbe et de se projeter sur un point plus près de X tel que f(X)=0.
la projection se faisant en utilisant la tangente à la courbe à chaque fois.

si x0 est un point de départ , la tangente en (x0,f(x0)) a pour équation
T(x0)=f(x0)+(x-x0)f'(x0)
la nouvelle abscisse que l'on cherche est donc
x1=x0-f(x0)/f'(x0) et ainsi de suite
x(n+1)=xn-f(xn)/f'(xn)

dans l'exemple qui suit , j'ai pris au hasard A/R² =0,5 et x0=0,2
On obtient dans ce cas
x0=0,2
x1=0,54368
x2=0,567315
x3=0,56753978
x4=0,5675398


graphique à suivre si j'y arrive.

[ansset]

erreur latex

[ansset]

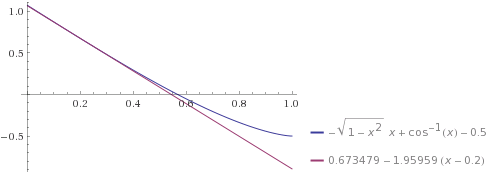avec donc A/R² =0,5
donc la fonction démarre en pi/2-0,5 et fini en -0,5
je part de x0=0,2 puis je suis la tangente partant de (0,2,f(0,2)) jusqu'au au point x1, qui se rapproche déjà très près du but.
et on recommence.

mon graphique ne représente que la première étape.

[Jeryko]

Bonjour à tous,

@Dlzlogic : Merci pour être le 1er à m'avoir mis sur la voie et pour le suivi.

@ansset : Merci pour ce temps encore plus important que tu m'as consacré.
Avec tes derniers messages, les choses sont maintenant limpides et je devrais m'en sortir " les doigts dans de nez".
C'est un véritable cours particulier. Je n'aurais pas pu trouver mieux détaillé et personnalisé, même dans un livre.
Il ne me reste plus qu'à transcrire cela dans mon tableur.

Aujourd'hui ce ne sera pas possible, je dois partir cet après midi, et cette fin de semaine non plus.
Pas avant le début de la semaine prochaine.

Encore merci à vous. Un véritable plaisir d'apprendre(1) ou de réviser avec vous.
Cordialement
Géry

(1) Je ne me souviens pas avoir étudié cette technique. Alzheimer me joue déjà des tours ?

[ansset]

(1) Je ne me souviens pas avoir étudié cette technique. Alzheimer me joue déjà des tours ?

cela ne peut s'appliquer pour toute fonction ni en partant de n'importe quel point.
on vois bien ( par exemple ici ) qu'on ne prendre un point de départ ou la dérivée est nulle. ( ici x=1 )
de même , pour une fonction qui a des dérivées nulles, et qui s'annule entre les deux, il faut partir d'un point à l'intérieur de ces deux extrêmes....

[mécano41]

Bonjour,

Une solution par dichotomie en VBA EXCEL (on pourrait aussi utiliser le solveur)...

Jeryko : j'ai fait ,il y a quelque temps, des applis EXCEL pour une cuve à fonds bombés en anse de panier, verticale ou horizontale. On peut entrer le volume et trouver la hauteur ou l'inverse. Egalement, pour un fût cylindrique incliné ... en cas de besoin, dis-le moi

Cordialement

[Jeryko]

Bonjour à tous,

Je n'ai pas pu résister ... je m'y suis mis entre "la poire et le fromage"
ça roule et ça marche !

@Dlzlogic : Bon anniversaire bientôt. !
@mécano41 :
Je découvre ton message. Je vais voir cela de près. Merci.
(Je pensais qu'on ne pouvait pas mettre de fichiers.zip en PJ ?) J'ai vu également pour d'autres xls, ...

[Jeryko]

Bonjour à tous,

@mécano41
J'ai vu ton fichier Excel macros/VBA. Pas mal mais je vais en rester là sur cette affaire.
Je le conserve "sous le coude". J'avais juste un besoin pratique et je voulais approfondir un peu.
Je connais aussi le VBA (à peu près) mais je n'en voulais pas. Je voulais utiliser uniquement les formules de base.
Sur une vue de profil, j'aurais souhaité afficher le niveau variable en couleur mais je pense que c'est impossible avec les formules.
Je sais le faire en VBA.

Merci encore.
Cordialement.