Bonjour,
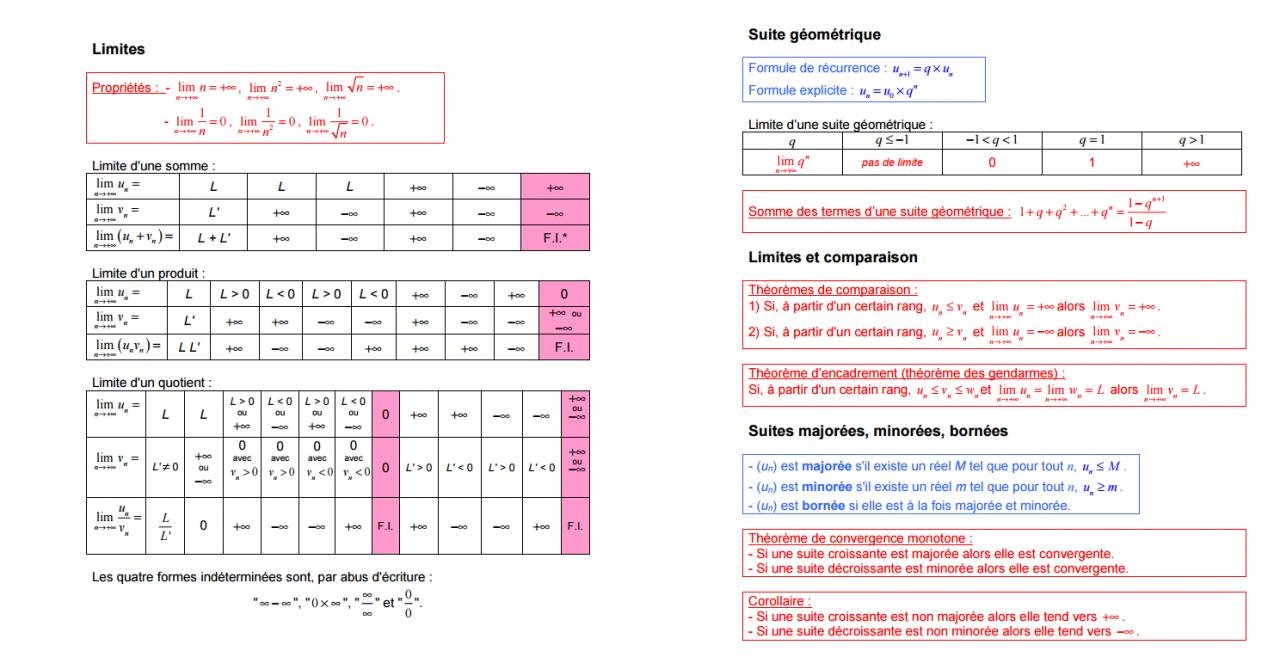
Je voudrais savoir les différentes méthodes pour trouver les limites d'une suite quand nous sommes face à un indétermination. En faite, je voudrais faire un tableau condensé pour savoir qu'elle méthode utiliser rapidement.
Je vous remercie,
Cordialement.
bjr,
quelle indétermination ou quel type ?
un exemple serait bienvenu.
merci
Cdt
Bonsoir BaptisteBaptiste.
Je te met ici en pièce jointe ce que j'ai. Néanmoins une simple recherche sur ton moteur de recherche favori aurait suffit.
Je reste à ta disposition pour d'éventuel question.
Cordialement.
*** lien serveur externe ***
Dernière modification par Médiat ; 11/05/2017 à 13h43.
Merci à vous !
Mais j'avais une question, on n'a 1/x=0 quand x tend vers + l'infini ( ou - l'infini). Donc par exemple 1/x + 2 quand x tend vers + l'infini vaut "2", mais quand on n'a " x/2", est-ce que ce quotient, quand x tend vers + l'infini ( ou - l'infini) vaut 0 ?
Logiquement oui, si on doit partager une quantité infiniment grande, cela devrait retomber sur 0 ?
Merci à vous,
Cordialement.
ben oui, et ce n'est pas une indétermination dans ce cas.Envoyé par BaptisteBaptiste
pardon:
edit quel rapport entre 1/X et x/2 ?
que veux tu dire ?
donc complément :
1/x tend vers 0 si x -> +/- l'inf
x, 2x, etc tendent vers + ou - l'inf selon le signe de x.
Merci Ansset.
Le problème, c'est qu'il y a des suites dont je ne comprends pas la méthode, par exemple:
Un= cos(n)/ n+1, et je veux trouver la limite de cette suite.
Dans la correction on indique cela:
Pour tout n appartenant à N, -1 ( inférieur ou =) cos(n) ( inférieur ou égal) à -1 ( Je m'excuse, je n'ai pas ls notations sur les claviers...)
Donc -1/n<cos(n)/n + 1< 1/n ( du coup, pour cela face moins sale le "<" signifie inférieur ou égal à"....)
( Bon après, on peut trouver la limite facilement), mais, pourquoi on n'a pas diviser "1" par "n + 1" ? L'inéquation ne changerait pas ?
encore une fois, il n'y a pas d'indétermination ici.
tu peux écrire la suite sous la forme que tu veux , cela ne change rien.
bref ! tj pas compris ou serait la gène ... un "vrai" cas d'indétermination !
Bonjour
il faut se souvenir queest une fonction bornée
En effet,
de plus
tu peux te contenter de ce résultat pour ton calcul de limite c'est amplement suffisant
pour la correction, ils ont simplement majorer minorer... :
comme le dit ansset ce n'est pas un cas d'indétermination
bon courage,
Dernière modification par fartassette ; 11/05/2017 à 14h18.
Merci à vous,
Je me suis fait peur en voyant la correction.
Pas facile de savoir qu'elle méthode utiliser chaque fois. Théorème de gendarmes, de comparaison etc...
Edit post #9"
petite correction, erreur de signe,ton résultat reste le même la suite tends vers o
crdlt
C'est bien pour cela qu'on fait des exercices, pour acquérir de l'expérience.
Par contre, s'il existe des méthodes adaptées pour certaines situation, il n'y a pas de règle globale, celles du cours sont à avoir suffisamment en tête pour penser à la bonne méthode (quand il y en a une).
Enfin il faut savoir que certaines limites sont très délicates à calculer et que tu ne vois ici que des méthodes très élémentaires.
Cordialement.
Merci
En faite, dès lors que nous sommes en présence d'une suite que l'on peut "encadrer", on peut utiliser ce théorème pour trouver sa limite. De meme si elle peut etre comparée.
quand on peut l'encadrer avec des valeurs qui convergent entre elles, oui.
mais généralement ( en cas "d'indétermination) on se retrouve avec des "0*(+l'inf) ou ce qui revient au même ( des "0/0" ou des "+l'inf/l'inf" )
indépendamment du signe ( que l'on trouve facilement ) il faut se souvenir qu'en cas A(x)/B(x) ( ce qui revient encore une fois à des A(x)*(1/B(x))
en + l'inf ( mais on peut retourner la situation si c'est en 0 en posant x'=1/x)
-une puissance supérieure est prédominante : x^p >> x^q en l'inf. ( si p>q )
-qu'une puissance est tj << à l'exponentielle
-qu'un log est tj << n'importe quelle puissance.
quand tout cela ne se retrouve pas dans les expressions , il existe aussi le théorème de l'Hospital en 0 , on passe aux dérivées .....
Bonjour,
Merci pour ta réponse.
Par exemple ici, on cherche la limite de: (n2 + (-1)n) Alors, je précise que le "2" représente le carré, je ne l'ai pas sur mon clavier.... Désolé qui cela fait "brouillon" ( en gros: "n" carré + (-1)puissance "n").
Dans le correction, au départ, on peut utiliser le théorème de comparaison:
(-1)n sup. ou = -1
n2 + (-1)n sup ou = à n2 -1
Mais on peut aussi utiliser le théorème des gendarmes non ?
(-1)n est compris entre -1 et +1, du coup:
n2 - 1 <n2 + (-1)n < n2 + 1 ( le "<" signifie sup. ou = à, désolé là aussi pour les notations...)
Cordialement.
Bonjour
En mode "répondre", ou en mode avancé si tu a cliqué sur réponse rapide, tu as des boutons x² et x2 pour les puissances et les indices.
On peut effectivement utiliser le théorème des gendarmes si on veut faire le malin. mais comme le théorème de comparaison suffit, une seule inégalité suffit. le théorèmes des gendarmes n'a d'intérêt que pour les limites finies.
Cordialement.
Merci.
Mais pourtant ici la limite est infini, de meme que parfois on utilise le théorème des gendarmes quand la limite est infinie...
Théorème 1. : Soient (un) et (vn) deux suites de nombres réels convergentes et ayant pour limites l et l' respectivement. S'il existe un rang n0, tel que :
pour tout entier n⩾n0 : un⩽vn , alors l⩽l ' .
Cordialement.
Ta remarque n'st pas claire, puisque tu évoques au départ une suite non convergente , puis tu cites un théorème qui fait référence à deux suites convergentes !???
bref , pas compris .
Cdt
Donc le théorème de comparaison c'est uniquement pour les suites convergentes ?
Cordialement.
Au départ oui!
mais en prenant une contraposée par exemple , on peut aussi en déduire aussi des divergences.
Merci ansset.
J'avais une question à propos de cela: Il faut trouver la limite de 3/n carré
Soit un intervalle )-a;b(, avec a>o et b>0.
La suite "Un" appartient à )-a;b( si et seulement si -a<3/n carré<b, c'est à dire 0<3/n carré<b, ce qui revient à n carré/3>1/b, soit n carré >3/b donc n>racine de 3/b.
Ma question est la suivante: Pourquoi on inverse la fraction ? Parce que je ne vois pas de fonction inverse, "un" est bien sur l'axe des ordonnées, je ne vois le rapport entre cela: a<b alors f(a)>f(b). Je parle des variation de la fonction inverse.
Cordialement.
justement la fonction inverse est décroissante .
donc si 0<(3/n²)<b alors (n²/3)>(1/b)
Oui mais 3/n2 est bien situé sur l'axe des ordonnées ? Il représenterait alors un nombre sur l'axe des abscisses ?
Car a<b donc f(a)>f(b), ce sont les images que l'on "inverse", donc ici 3/n2, étant donné qu'il est "inversé", ce serait un nombre sur l'axe des abscisses ?
Cordialement.
BaptisteBaptiste,
les nombres sont des nombres, pas des points. 3/n² est un nombre, on peut le prendre aussi bien comme ordonnée d'un point du plan, comme abscisse d'un point sur l'axe (Oy), que comme abscisse d'un point du plan ou comme abscisse d'un point de l'axe (Ox), voire même comme longueur d'un segment, mesure d'un angle ou tout autre usage des nombres réels. Même chose pour son inverse, qui est un autre nombre.
Cordialement.
Merci gg0.
En faite le nombre 3/n2 m'a fait penser à une fonction de type 3/x2, du coup, ce 3/x2 est une image (f(x)) donc placé sur l'axe des ordonnée... Ici je pensais que "Un" était une image...
Cordialement.
En fait, les suites étant des fonctions particulières, les Un sont bien des images, mais il faut absolument que tu déconnectes la fonction et sa représentation. f(x) est un nombre, si on lui applique une autre fonction, ce sera un antécédent. Si f(x)= 2, il y a des points notés "2" sur les deux axes, et bien d'autres usages de 2.
D'accord, merci gg0.
Par exemple: f(x)= 2x + 3, la variable x, qui est donc un antécédent, peut valoir x2 + 1 par exemple ou encore 8 racine de 5 etc...
Sinon, concernant le la suite Un=3/n2, c'est une fonction inverse de type k/u ( ou 1/u) ou K est une constante et "u" une fonction.
Cordialement.
