exercice nombres complexes Terminale S

[yakitori]

bonjour
J'essaye d'aider ma fille à faire cet exercice mais je n'y arrive pas moi même:
montrer que l'equation suivante a une solution imaginaire pure.

pouvez-vous m'expliquer comment le faire svp?
cordialement
-----

[gg0]

Bonjour.

On pose z=ib avec b réel, on remplace, et on vérifie qu'il y a au moins une valeur de b qui convient (rappel : le complexe 0 s'écrit 0+i.0).

Cordialement.

[yakitori]

merci gg0 j'ai fait ça mais j'arrive jusque là:

ensuite je suis bloqué

[gg0]

(rappel : le complexe 0 s'écrit 0+i.0)

Ecris le premier membre sous la forme a+ib.

[A voir en vidéo sur Futura]

[yakitori]

comme ça?

[gg0]

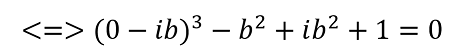
Ben ... ce n'est pas de la forme a+ib, ,disons u+iv avec u et v réels.
C'est quand même la base du cours qu'on peut écrire tout nombre complexe sous la forme un réel + i fois un réel.

NB : Evite les pièces jointes, tape directement ( b² ou b^2, b^3, ou avec la bascule x² des modes "répondre" ou "avancé"), car j'ai été obligé d'attendre que la pièce jointe soit validée pour pouvoir la lire.

[andretou]

merci gg0 j'ai fait ça mais j'arrive jusque là:
Pièce jointe 354946
ensuite je suis bloqué

Bonsoir Yakitori
Tu peux développer ton expression au #3 et regrouper les termes de façon à obtenir une égalité de la forme A + iB = 0
A partir de là tu vas pouvoir déterminer les valeurs de b telles que A = 0 et B = 0

[fartassette]

Bonjour,


Yakitori a certainement trouvé la solution en posant la forme algébrique de ce complexe. Sauf erreur on peut résoudre cette équation sans y avoir recours, juste en factorisant un peu ( un des facteurs s 'annule bien ,la solution semble évidente)?Peut être que ce n'est pas suffisamment rigoureux?

[gg0]

Tiens ! je ne vois pas cette factorisation ! Je baisse !

[fartassette]

bonjour ggo

j 'ai écris un produits de deux facteurs.Bien sur je répète sauf erreur

[andretou]

Bonjour fartassette
J'aime beaucoup ta méthode qui est chaque fois surprenante, merci là encore de nous l'avoir fait partager !
Cependant je t'avoue que pour moi la solution ne semble pas vraiment plus évidente dans cette dernière étape que dans l'équation initiale... Mais rien que pour le style, j'en redemande !

[gg0]

Ok,

je comprends mieux pourquoi je n'y arrivais pas : Moi, je respecte les règles des maths. Par exemple, je n'écris pas de racines carrées portant sur autre chose que des réels positifs (c'est dans la définition de la racine carrée).

Comme ton équivalence finale n'est que le fait de voir que i est solution (pas de calcul) et de plus est fausse (le sens direct est faux), finalement tu n'as fait que cacher sous des simili calculs une intuition (ou le résultat obtenu par une méthode correcte).

Dommage !

[fartassette]

D'accord , j'en prends bonne note ggo


j'avais en tête que la solution devait impérativement être unique et qu'elle appartenait à .De ce fait, la construction d'un produit pour faire apparaître l'unique solution est le chemin le plus simple à mon sens ,d'autant plus que la factorisation est très simple.Oui intuitivement, la partie réel étant nul implique que mon résultat sera seulement composé de ib. l'implication, l’équivalence et tous les rudiments de la logique sont pour le moment source d'embrouille dans mon esprit .Je reconnais volontiers que ce raisonnement n'est pas suffisamment rigoureux .

c 'est ce sens ? merci


merci Andretou c 'est sympa j'avoue qu' il me manque de la rigueur ..j 'apprends en même temps

[gg0]

Bon, tu n'as pas compris : "d'autant plus que la factorisation est très simple" Elle n'est pas simple, elle est fausse, sauf justement si z=i, car alors sous la racine carrée il y a 1 (*). Sinon, il n'y a pas un réel positif.
Comme tu le dis, "ce raisonnement n'est pas suffisamment rigoureux". Il ne vaut pas grand chose comme preuve.

le sens qui pose problème n'est pas . Si z=i, alors on peut écrire l'égalité et elle est vraie. Mais dans l'autre sens, on ne peut même pas, à priori, écrire l'égalité.
La rigueur commence par ne pas écrire n'importe quoi.

Cordialement.

NB : "j'avais en tête que la solution devait impérativement être unique" ?? Ce n'est pas dit dans l'énoncé. "un" est un article indéfini.

(*) ou d'autres valeurs particulières de z, de la forme a+i avec a supérieur ou égal à 1)

[fartassette]

un peu déçue d 'avoir proposé ceci

merci pour l'analyse

[andretou]

un peu déçue d 'avoir proposé ceci

Pas moi...

[yakitori]

merci beaucoup j'ai compris:!
1-b^2 + (b^2-b^3)i = 0
<=>1-b^2 = 0 et b^2 - b^3 = 0
<=> (b = 1 ou b = -1) et b^3 = 1
<=> b = 1

[gg0]

Voilà, c'est ça.

Cordialement.

[phys4]

Annulé.....