Géométrie dans l'espace

[Nonimamie]

Merci mais est-ce correct la réponse de la question 2 ?
-----

[ansset]

D'accord, merci, j'ai compris.
Pour la deuxième,
Si K' est l'intersection de (P) avec la droite (AE)
alors la droite (HK') app au plan (P)
La droite (JA) appartient au plan (AIJ). Puisque ces deux plans sont parallèles, les droites le sont aussi car elles appartiennent au plan (ADH).

erreur de frappe ? : Si K' est l'intersection de (P) avec la droite (CG) !! pas la droite (AE)
mais as tu bien vu que tout cela est directement lié à la propriété 15 du lien que je t'ai donné ?

[Nonimamie]

Oui, je suis désolée ... Oui, je pense avoir compris. On déduit que deux droites sont parallèles grâce aux plans qui le sont également grâce à la propriété :
"Si deux plans sont parallèles, alors tout plan qui coupe l'un coupe l'autre et les intersections sont des droites parallèles. "

[Nonimamie]

Pourriez-vous m'indiquer ce que je dois précisément effectuer pour la construction (dernière question) ?

Merci

[ansset]

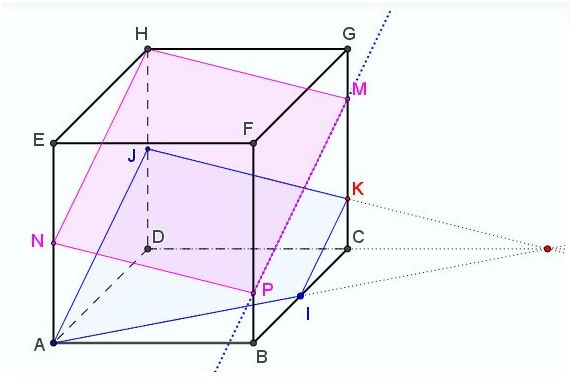
commencer par dessiner l'intersection du plan P avec le cube.
On voit vite que le polygone a quatre coté, ce qui donne déjà un premier nom.
ensuite regarder si celui ci a des propriétés particulières , afin d'en préciser la nature.

[Nonimamie]

Voilà, j'ai tracé la section du cube (hachurée en rouge). Merci de me dire si cela est correct.

La section du cube par le plan (P) est le quadrilatère HLMN. Comme (HN) et (LM) sont parallèles, HLMN est un trapèze. Merci de me préciser si mon raisonnement est juste.

[ansset]

tout à fait pour moi !

[Nonimamie]

Merci !
Est-il nécessaire de préciser que le plan (LMN) coupe l'arête (FB) en un point que je dois nommer ?

Pouvez-vous également me dire si mes réponses sont assez complètes :
1)Si K' est l'intersection de (P) avec la droite (CG) alors la droite (HK') appartient au plan (P)
La droite (JK) appartient au plan (AIJ).
Comme ces deux plans sont parallèles , les droites aussi, car elle appartiennent au même plan (DCG).

2)Si K' est l'intersection de (P) avec la droite (CG) alors la droite (HK') appartient au plan (P)
La droite (JA) appartient au plan (AIJ). Puisque ces deux plans sont parallèles, les droites le sont aussi car elles appartiennent au plan (ADH).

[gg0]

Heu ... NM est à l'intérieur du cube, la section n'est pas HLMN : une section est l'intersection avec les faces du cube.

[Nonimamie]

Est-ce que la figure ne serait pas plutôt celle-ci ? On obtient alors un cube ...

[ansset]

pourquoi un cube.
l'intersection est forcement plane et ici à 4 cotés, mais ses spécificités sont encore plus importantes que pour un trapèze.

[Nonimamie]

Oui, excusez-moi, il s'agit d'un rectangle... Ma deuxième figure est donc celle qui est juste ? Comment faut-il faire pour le démontrer ?

[ansset]

oui, cette figure est bonne.
je pensais avoir corrigé mon post #40 qui était faux, car N n'est pas sur l'arête du cube et donc la surface de l'intersection entre le plan et le cube va au delà du segment MN ( mais j'ai du oublier de poster ma correction )
je suis désolé de cette erreur de ma part.
maintenant, ton nouveau polygone a des propriétés encore plus fortes que le trapèze évoqué plus haut.

qu'entend tu par "carré" , l'intersection n'est pas un carré.

[Nonimamie]

Il s'agit d'un rectangle ? Comment le justifier ?

[ansset]

messages croisés:
pourquoi serait ce un rectangle ? il faudrait des angles droits !

[Nonimamie]

Il s'agit d'un parallélogramme mais comment le justifier ?

[Nonimamie]

Par définition, (HN) est parallèle à (MP) (ils sont sur les arêtes du cube) donc HN = MP. C'est un parallélogramme. Est-ce cela ?

[ansset]

c'est bien un parallélogramme parce que on a à la fois
(HM) // (NP) ET
(HN) // (MP)
cela est juste nécessaire et suffisant.

le HN=MP est vrai si on parle de vecteurs, c'est exact, mais pas dans l'esprit de ton exercice.
et les deux droites ( elles ) ne sont pas // parce qu'elles sont sur des plans // , cela ne suffit pas.
( et elles ne sont pas sur les arêtes du cube )

en revanche , tu peux aussi montrer que ce parallélogramme n'est pas un carré.

[Nonimamie]

Merci mais que dois-je encore démontrer pour que ce soit un parallélogramme ? Juste le fait que les droites soient parallèles ? Ou bien de même longueur ? Ou que ce n'est pas un carré ?

[ansset]

voir ici la définition première du parallélogramme , ainsi que d'autres définitions équivalentes.
ici , la première est la plus simple à utiliser:
https://fr.wikipedia.org/wiki/Parallélogramme

le fait que ce ne soit pas un carré ne prouve pas que c'est un parallélogramme
.
en revanche , il peut être implicitement demandé de montrer que ce n'est pas un carré, ni même un rectangle ( qui est un cas particulier de parallélogramme )

[Nonimamie]

Si un plan (NHM) est sécant à 2 plans parallèles (EHD) et (FGC), alors les droites (HN) et (MP) sont parallèles. Et après, comment montrer qu'elles sont de même longueur ?

[ansset]

les deux parallélismes ( des droites opposées ) suffisent, (*)on peut en déduire l'égalité des longueurs , mais c'est inutile.
reste que tu ne montres pas que ton parallélogramme n'est pas un rectangle.

(*) je t'ai même mis le lien qui donne cette définition première du parallélogramme.

[gg0]

M'enfin (*) deux côtés parallèles et de même longueur, ça ne fait pas obligatoirement un parallélogramme. Comme on voit les parallélogrammes en début de collège, si tu ne te souviens plus de ce que c'est, va voir une définition. Avec Internet, tu n'as aucune excuse de ne pas l'avoir fait.

NB : Poser les mêmes questions sur 2 forums différents ne rend pas justice à ton intelligence.

(*) comme dirait Gaston Lagaffe.

[Nonimamie]

Est-ce que cela suffit si je montre qu'il a des côtés opposés parallèles sans mentionner de longueur ?

[Nonimamie]

Si un plan (NHM) est sécant à 2 plans parallèles (EHD) et (FGC), alors les droites (HN) et (MP) sont parallèles.
Si un plan (EHD) est sécant à 2 plans parallèles (HGC) et (EFD), alors les droites (HM) et (NP) sont parallèles.
Or, si un quadrilatère a ses côtés opposés parallèles alors c'est un parallélogramme.
Par conséquent, HMNP est un parallélogramme.

Est-ce que cela suffit ?

[gg0]

Ben oui !

Cordialement.

[gg0]

Sauf qu'une rédaction plus claire est possible :

le plan (NHM) coupe les 2 plans parallèles (EHD) et (FGC) suivant les droites (HN) et (MP); donc (HN) et (MP) sont parallèles
le plan (EHD)....

Dans ta rédaction, (HN) et (MP) arrivent sans raison, comme un cheveu dans la soupe, tu n'en as pas parlé avant. Tu demandes donc au lecteur d'imaginer ce que tu as dans la tête. Ce n'est pas à lui de chercher, c'est toi qui dois expliquer.

Cordialement.

[Nonimamie]

Pour résumer,
le plan (NHM) coupe les 2 plans parallèles (EHD) et (FGC) suivant les droites (HN) et (MP); donc (HN) et (MP) sont parallèles
le plan (NHM) (et non EHD c'est une erreur de ma part) coupe les 2 plans parallèles (EGC) et (EFD) suivant les droites (HM) et (NP); donc (HM) et (NP) sont parallèles

Je n'ai pas besoin de démontrer que ce n'est ni un carré ni un losange ?

[gg0]

C'est toi qui vois. Et tu regardes sur l'autre forum si tu décides de le démontrer.

NB : Lis l'énoncé.

[Nonimamie]

Mais je ne comprends pas comment faire, je ne connais aucune longueur ... S'il-vous-plait, c'est ma dernière question, je réfléchis à cet exercice depuis lundi, pourriez-vous m'aider encore un peu ?